On Methods of Technical Analysis and Market Forecasting

The article is prepared based on a theoretical and practical study carried out by Stairway to Heaven LLC and contains an original part of supporting documentation to the analytical system The Wild Cat's Strategics® for MetaTrader 4. Stairway to Heaven LLC has copyright on The Wild Cat's Strategics® for MetaTrader 4 which is successfully registered by the Russian Federal Service for Intellectual Property, Patents and Trademarks. The copyright on this publication belongs to the author of the article who is a developer of the system. The program code as attached hereto is based on some scripts and indicators published earlier whose authors are included in the code as copyrighters.

Introduction

This article will briefly outline a general problem and gradually resolve a set task unveiling basic principles of the concept and forming the backbone of the new outlook on financial markets, technical analysis and trading paradigm per se.

Since the solution allows for alternative implementations of the part of the task that is already copyrighted, one of the goals of the article is to draw the developers' attention to studies and search for other solutions that may be more advanced and/or more interesting.

Traders are offered a ready to use technical tool for analysis and forecasting. This tool is a next stage of development of the Extended Regression StopAndReverse indicator published in 2007 which has received recognition from lots of users. That said, the program code of the tool can be used by developers as an end module of data presentation in their own solution implementations.

1. Overview of Infrastructure. General Concept

1.1. Setting a task at large...

A fair number of serious works has already been devoted to the attempts to formulate a mathematical description of markets and various studies of internal and external dependencies of the financial instrument prices.

They bring us to an unpromising conclusion - markets have a great self-defense against determination and a clearly defined capability of 'seeping' through different science-oriented models that serve to ensure stability of forecast accuracy essential for practical trading for a period of time required by the majority of traders.

George Soros's words come to mind in this regard adequately summarizing this situation:

...they cannot obtain perfect knowledge of the market because their thinking is always affecting the market and the market is affecting their thinking.

Does it mean that it is impossible to develop a fully deterministic mathematical model of the market? Generally speaking, there is no point in seeking an answer to this question in practical trading as trading aspects are more characteristic of art rather than science. Science however has a great potential to support the entire trading process.

There are some scientific methods and approaches that can be successfully applied to working in financial markets. It is important here to lay special emphasis on the approach to such application itself. What is of importance to a trader? I would like to say a few words about the so-called Mechanical 'Black Box' Trading Systems (MTS) in passing. Although one can dwell on boon and bane of MTS, we are only interested in the ultimate conclusion which is not very encouraging either.

Since the majority of traders get easily trapped by MTS having to depend on principles, quality of the development and unavoidable errors in these programs, trading transforms from the art into a faulty mechanism whose defects are hidden and unpredictable.

Moreover, traders should have a good knowledge and clear understanding of when and what areas of price movements a certain MTS can or cannot be applied to. But this requirement is very often not met and traders get out of the habit of needing to analyze due to the seeming simplicity of using MTS. We will abstain from discussing MTS here, though.

Among other things, traders need a fairly accurate forecast to rely on and according to which to dynamically form and adjust their market activity. Forecasts can, in turn, be conventionally divided into two groups - forecasts in the form of various predictions based on some scientific methods and forecasts in the form of direct transfer of interpolated data.

To make it clearer, they can be exemplified by two curves built on charts sometimes looking very much alike. The first curve is built using the Singular Spectrum Analysis known as 'Caterpillar' in Russia; the second one represents a simple shifted moving average. These may of course be not the best examples but it does not matter at this point. We will not consider advantages and disadvantages of these two methods here; what is important is that both of them are used by different traders in their work with a certain efficiency.

In fact, both methods only differ in that SSA seeks to predict future changes in some parameters while calculation and display of the moving average does not predict anything - this method merely displays information on actual data computed in a simple manner. Strictly speaking, there is no prediction in the second case as such; the forecast is produced by a trader based on the price relative to the moving average being a forecast tool in itself. In both cases, a trader carries out some sort of analysis.

Thus, trading based on scientific forecasts serves to facilitate operations in the markets yet it is associated with greater risks as the forecast errors are corrected by traders with delay which is often unacceptable.

On the other hand, trading based on direct data transfer eliminates errors resulting from mathematical calculations/predictions but increases trader's intellectual effort. If we now take into account all the differences in psychology and mentality of the majority of traders and average them out, the trading results in the general case will show that in practice there is no particular difference between the two specified groups of forecasts.

A significant difference will start to become apparent when a scientific forecast technique will get too complex thus increasing the error probability, quantity and quality. One would think that there appears to be a conflict between the initial conditions and the final result.

Indeed, if it is decided to produce forecasts using scientific methods, simple techniques will not yield adequate results in terms of accuracy. How to avoid the increasing errors when techniques are getting complicated and can they be avoided altogether insomuch that they start affecting the required forecast accuracy? This is a tricky question that can easily lead to a logical deadlock or give rise to blunt solutions involving time-consuming enumeration of simple methods and their combinations.

Where and how to find the golden mean between the source and outcome, complexity of calculation methods and accuracy of end results? There may be a great number of solutions. At least one of them is going to be dealt with hereinbelow.

1.2. Splitting into parts...

Since we are focused on technical trading, the initial data is only limited by quote history, i.e. we have the total number of bars and four price values of every bar without volumes. Volume values shall be ignored as they vary greatly from one source to another and are not true to the volume of trades. Therefore there is no sense in using them in calculations since we will ultimately be getting different forecasts applying the same price data which in itself is in conflict with the given task.

On the other hand, price movements of the financial instrument under consideration already contain information on the actual, true trade volumes, being directly dependent on the latter. We will have to process the numerical series at hand and display the processed data on a chart.

Not to complicate the solution, the task will be divided into two parts - preprocessing of data using a certain scientific method and post-processing followed by data display. Let us tackle the task starting from the end.

1.3. Solving the second part of the task...

Assume, we already have preprocessed data that shall be displayed on a chart. What method, approach, data display technique shall be preferred to ensure the least distortion to be caused to prepared material while providing analysis with forecasting potential?

Mathematical apparatus offers an adequate range of sleek solutions among which we can single out and select the regression analysis as a method meeting the above specified criteria.

The regression analysis is a statistical method for studying dependencies which, from a certain standpoint, can be considered as a simple way of data presentation without corruption of the initial material. Another purpose of the regression analysis is prediction of values of the dependent variable. This method is virtually ideal for the given task.

So, can we consider the second part of the task solved? Not yet. The solution has only been outlined, now the type of regression has to be determined. Let us see what outcome we will have using the linear regression.

Assume that the initial plotting point obtained following the preprocessing of data is one of the local extrema of the EURUSD exchange rate at the end of Autumn 2007. A standard deviation channel will be plotted from this point using the central ray of the linear regression as a basis.

Figure 1. Channel of the standard deviation from the regression line plotted for EURUSD

What is the value of the produced forecast?

Channel trading rules are well known. Clearly, the value of the above forecast will vary from one trader to another; however such forecasts are known to be quite adequate in practice and are fairly widely used.

We are also familiar with the flaws of such forecasts. It is now that we know that the EURUSD rate steadily hit the upper limit of the channel and kept on rising freely. But traders at that time had to make a choice associated with risk and intense feelings.

This brings us to a fair question - can one of the purposes of the regression analysis related to prediction of values be used more effectively in forecasting to facilitate the decision-making in critical moments? Yes, it can. Data presentation for this purpose has to be based on the polynomial regression, where the extrapolated numerical series will be the target forecast, a prediction, a peculiar tip.

Let us plot the same standard deviation channel from the same point but based on the central curve of both the interpolated and extrapolated numerical series of the polynomial regression.

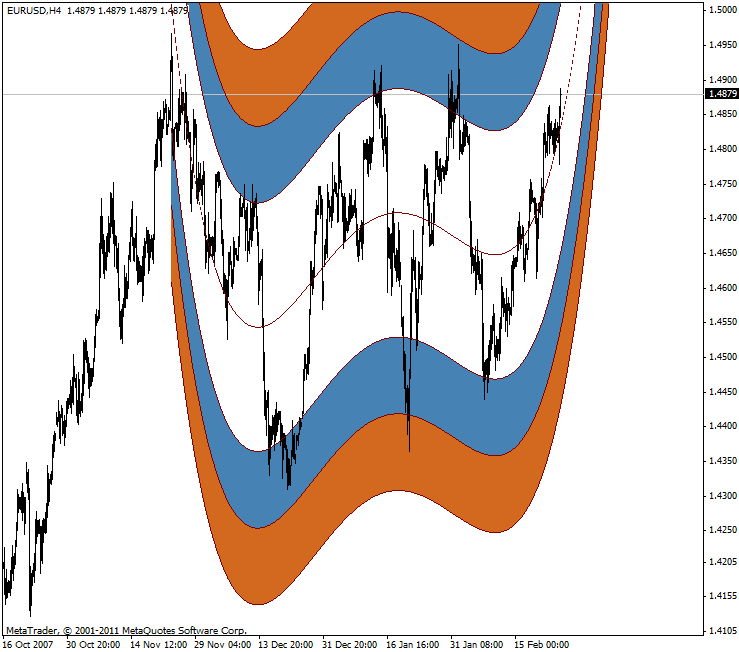
Figure 2. Channel of the standard deviation from the polynomial regression line plotted for EURUSD

Not bad. Exactly what a trader needs for a more confident and peaceful work. It should only be noted that an error in parameters of this method turns the respective forecast into its antipode. Such an error will certainly be a developer's fault and not characteristic of the method itself.

The method as such is impeccable in terms of the given task and we can now consider the second part of the task solved as we have decided on the data representation method.

Indeed, it is difficult to think of something more familiar and clear than a directed channel with standard deviation levels where the price moves along its vector. In this case, when compared to various linear channels, the forecast is more accurate while there is nothing new in the trading tactics as it is thoroughly studied and is even intuitively clear.

Here, we can look back at yet another aspect of the analysis. How to make it easier for a trader to make decisions on market entry, closing and/or reversal of positions? The factor of trading signals in the form of a "black box" brings about the same risks and adverse effects as MTS. The use of additional oscillators is individual choice and it is important here for a trader to realize and understand what exactly it is that any given indicator shows, otherwise he may also become a victim of the program.

What can mathematics offer to a trader in this respect? On the one hand, extrapolated data of the polynomial regression is a warning forecast per se which shall be used to determine entry/exit areas. On the other, a de facto standard Stop Loss level is a common practice in trading as it serves as a limiting factor for losses occurring as a result of inevitable errors in the market activity.

The display of dynamic Stop Loss levels on the chart is no big deal as the algorithm is simple and well-known. One only needs to decide on the method for calculation of levels and the notion of standard deviations showed itself here to good advantage. Calculation of the price deviation over the range from the already known initial point to the zero bar does not seem complicated either.

As a result, all information required for a technical analysis that can be obtained at this stage is directly available on the chart. Predicted Stop Loss levels in polynomial standard deviation channel appear as follows:

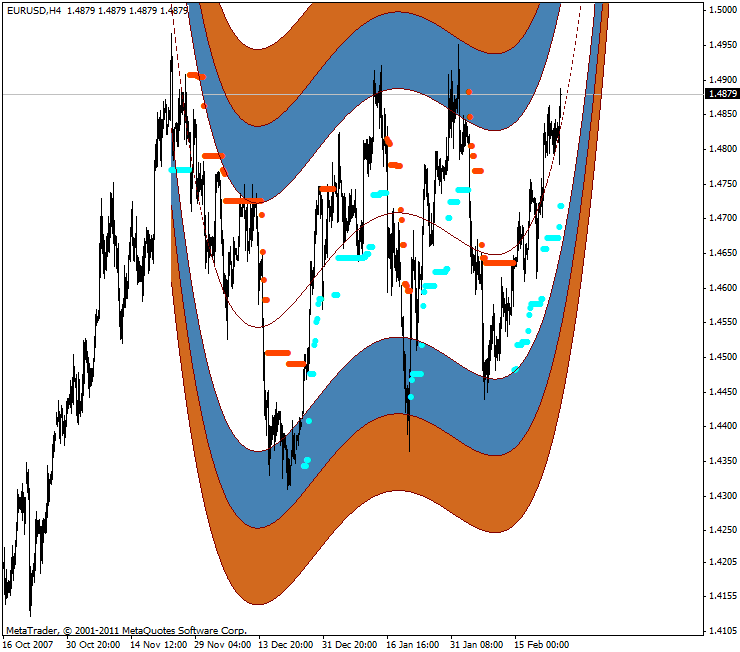
Figure 3. Predicted Stop Loss levels in polynomial standard deviation channel

And, a warning "polynomial forecast" in visual perception, respectively:

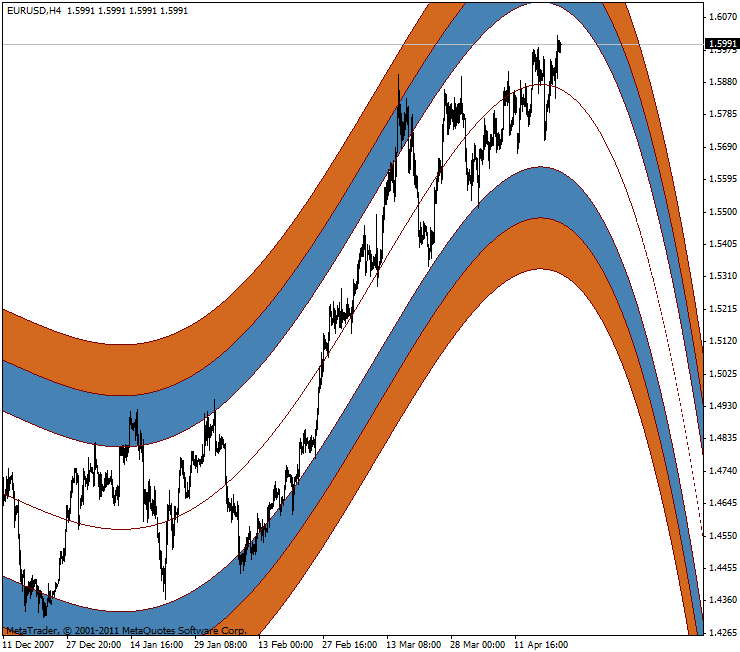
Figure 4. EURUSD price movement forecast in polynomial regression

The implementation of the final data representation in the form of MQL4 program code is attached to this article.

The module is completely ready for work and can be used as an independent technical tool. However its entire hidden potential and forecasting opportunities will show their worth to the fullest when used as a part of a single complex implementation of several components, as will be demonstrated hereinbelow.

The following material may serve as a guideline in searching for alternative solutions for preprocessing of data.

1.4. Solving the first part of the task...

It should be noted that the selected data representation option generally narrows down the remaining task to determining the initial, reference point which is another benefit of post-processing.

Indeed, the method of regression analysis saves us the trouble of complex physicomathematical synthesis at early stages and we do not have to distribute the price changes across a spectrum or drag in the superposition of harmonic components and other methods leading to certain fluctuations and distortions of end data as against the initial numerical series serving as a backbone for a more probabilistic forecast closest to reality.

However, the reference point can be determined using any method simply as a pointer to it. Nevertheless, the solution in question imposes fairly strict requirements to preprocessing, as the method on the whole, called the wave regression method, suggests the presence of deep loops as well as negative and positive feedback between its mathematical components.

Assessment of longstanding works performed by various researchers dealing with market laws and natural wave processes coupled with individual results first mathematically defined and further obtained in practice, leads us to a conclusion that there is at least one theory allowing to dynamically describe the market structure with an adequate degree of accuracy and predict future price changes based on this structure using the regression analysis.

This brings us to the wave theory that defines the so-called Elliott Wave Principle. Modern development of this theory gave rise to several independent branches, the fractal wave branch being more prominent as it has a lot of potential for relevant projects. This very branch was selected as a working hypothesis for the entire wave regression method.

1.5. Putting all components together

So, in the final variant of the solution, we have an implemented project of a mathematical method for defining and describing fractal wave structure of numerical series comprised of market quotes together with a method for the analysis of the obtained description of the structure and prediction of price fluctuations of the financial instruments under consideration.

That said, we do not need a separate reference point but a whole fractal structure since it defines the polynomial regression parameters and the status of the fractal in question using the trend/correction criterion.

Moreover, description of the structure allows to use additional linear tools on the chart, such as Fibonacci Retracement and Andrews' Pitchfork:

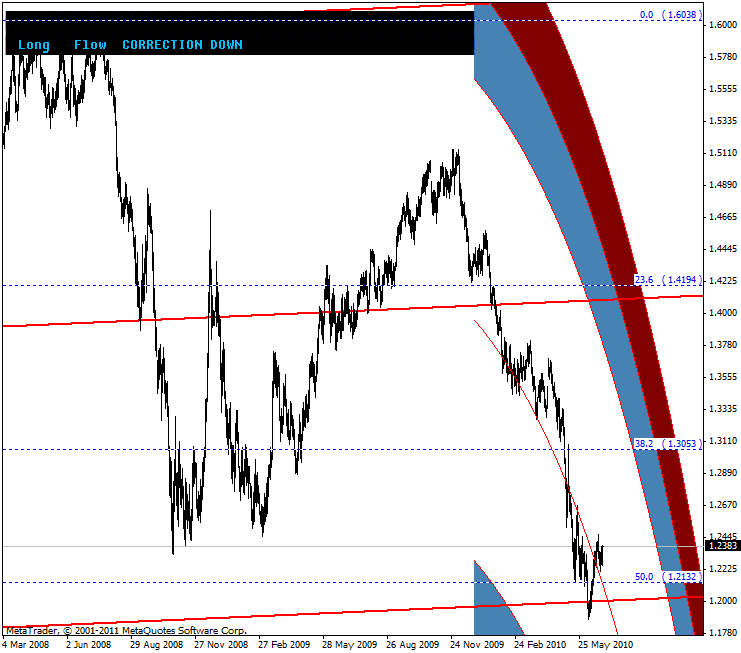
Figure 5. Additional tools (Fibonacci Retracement and Andrews' Pitchfork) for the fractal structure analysis

1.6. Fractal wave matrix

Development of the modern fractal wave theory laid the basis for a motivated empirical research of different phenomena, both physical and economical.

Results of that research were transformed into a relevant form of mathematical data following which the so prepared data was considered in terms of application to the real market and properly classified. For a whole identified group of stable fractals, a unified matrix was created adapted for use as initial data for polynomial regression calculation.

It is known that a fractal represents a stable structure that is scalable and repeated in any of these scales. In fact, this should mean that fractals of the same type will be fairly similar in form on a monthly time frame and a tick chart. In the real market conditions, the internal structure of fractals is however exposed to destruction and distortion. The shorter the time frame, the more often it can be observed.

The fractal's structure is made up of other fractals similar or not similar to each other in the exterior form. Chaotic price movements customarily called the market noise are more intensive on shorter time frames. When the market noise level exceeds a certain limit, the fractal structure breaks down.

The fractal's form gets distorted insomuch that it falls out of a set of certain stable fractals. The limit of the market noise level on longer time frames is higher and fractal structure gets much more stable.

The above allows us to draw an important intermediate conclusion that requires comprehension and attention in work and analysis - even if the fractal structure gets broken down and destroyed on shorter time frames, the price will still be moving within the framework of senior fractal formation. This conclusion is essential in trading over any period of time as it unlocks potential for orientation in the market situation.

1.7. Market cash flow concept

In practical trading, there is no point in considering low-level prerequisites for the emergence of stable fractals in the market - they are transparent and have no effect on the quality of work and the amount of profit whatsoever.

On the top, user level, it is expedient to consider and determine important primitive fractals affecting the price movement in the near future and orienting traders in the current situation.

This will further be exemplified but fractals should first be presented in a way that would be clear, natural and customary for every trader, regardless of their knowledge and background. There is a direct analogy to rivers, their tributaries, sources and other natural characteristics.

A developing fractal structure on every time frame forms equilibrium cash flows that remain stable for a certain time. Imagine a pool with two pipes - filling and discharge. The first pipe is constantly filling the pool that is constantly leaking water from the second one. Apparently, the volume of inflowing water shall be equal to the outflowing volume in order to ensure the stable water level in the pool.

Market flows are formed in a similar way, out of the total of inflowing and outflowing money stock over a dynamically changing range of bars on a given time frame. Newton's First Law (Law of Inertia) is also applied here which has sure been repeatedly observed by every trader - in the thin market, when the aggregate volume of money stock is not big, the price is quite easily affected by small amounts invested in the market by market players.

There is a great number of such flows being formed but by far not every single one of them is appropriate to be considered individually. Experience and common sense suggest that the optimal number of separated flows is three for each time frame.

One of them shall represent the main flow, the river flowing on any given time frame. The other two are the river arms or else the internal flows or additional filling and discharge pipes - whatever is easier to comprehend. Wave regression channels can be interpreted as banks of the river and its arms or figurative boundaries of the flows, or pipe casings, respectively.

The entire concept is crowned with a postulate of the existence of a global or, in other words, fundamental flow - the main river for the study of a financial instrument as a whole. Such flow is made up on the basis of the total money stock available in the market and relevant to a particular financial instrument. This flow is obviously the most inertial one and all the price movements and the entire development of various fractal structures take place inside the fundamental river banks.

Thus, the cash flow concept considerably eliminates the uncertainty of price movements and along with the wave regression channels provides a trader with additional benchmarks in the market topology as well as analysis and forecasting means.

2. Elementary Fractals as the Driving Force of the Market

2.1. Primitive fractals

A primitive fractal is a material for trend and correction patterns. It is formed by three consecutive chart extrema and can therefore be defined as the minimum possible (primitive) stable repeated structure.

Primitives permeate all and any time frame and form a structure of the entire set of fractals in the wave matrix. One can only define four of such primitives as there is simply no other.

Let us have a look at all four primitives following each other in the same flow. Three points (А-В-С) have formed an uptrend pattern. This fractal has only three key characteristics:

1. The extremum point B is higher than the extremum point A.
2. The extremum point B is higher than the extremum point C.
3. The extremum point C is higher than the extremum point A.

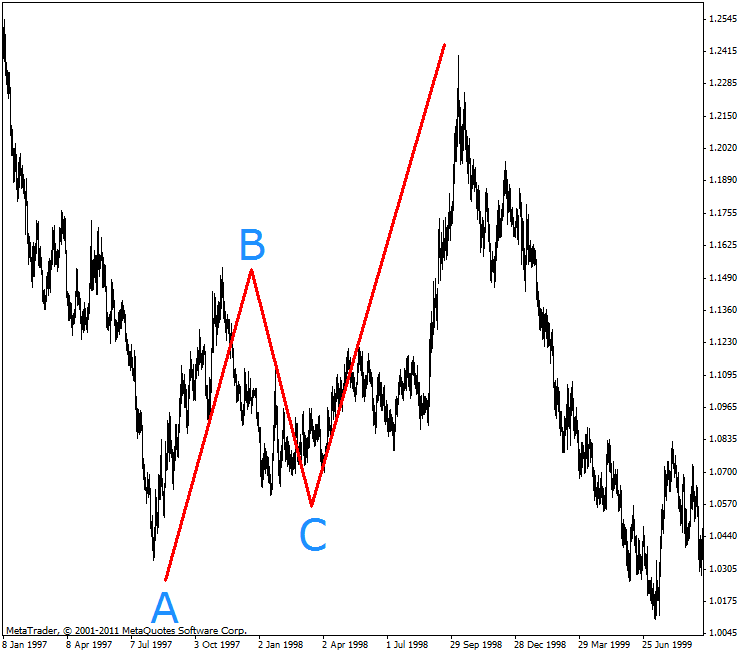
Figure 6. Uptrend pattern

The emergence of such elementary structure on any time frame from М1 to MN1 is a clear indication of the uptrend following in the same flow where the primitive fractal was formed. However, unless and until the fluctuating price rises above the point B and goes beyond the boundaries of the formed primitive, the uptrend will be unconfirmed and unstable. In our case, we can observe the uptrend formed and confirmed.

Rule: a confirmed uptrend is followed by a downward correction in the same flow.

The rule leaves no alternative whatsoever - if there is a formed uptrend in the flow and such uptrend is confirmed, it can only be followed by a downward correction in the same flow, without exception.

This implies that any uptrend upon its confirmation forms the next pattern, an elementary structure of the primitive fractal preceding the downward correction. This fractal also has only three key characteristics:

1. The extremum point B is lower than the extremum point A.
2. The extremum point B is lower than the extremum point C.
3. The extremum point C is higher than the extremum point A.

It should be borne in mind that a confirmed trend is always followed by a correction which does not necessarily take place exclusively after the confirmed trend as there are also other options.

Nevertheless, the emergence of such elementary structure on any time frame is a definitive sign of the following downward correction in the same flow where the primitive fractal was formed. Here is an illustration to this case:

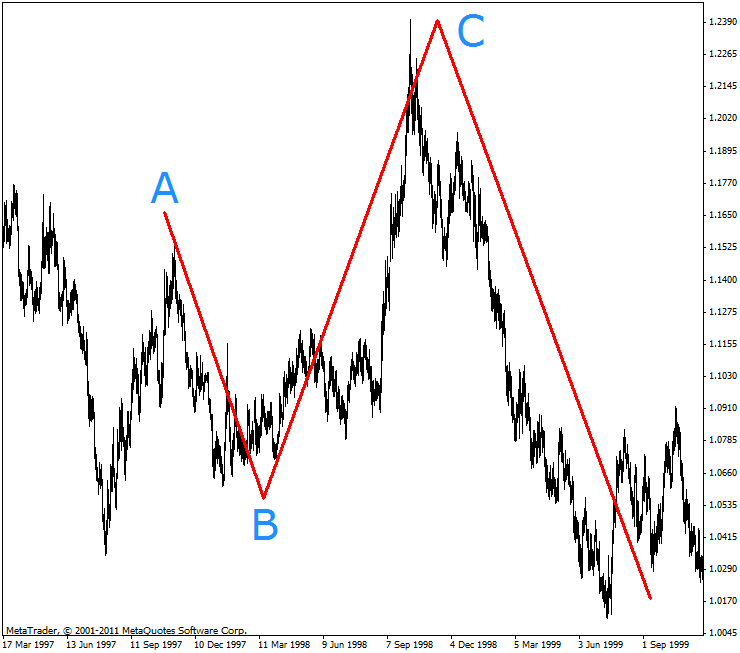
Figure 7. Downward correction

The following three extremum points have formed a pattern for an upward correction. As can be seen, the correction in this case follows the correction and not the trend. This fractal like the two primitives considered earlier, also has only three key characteristics:

1. The extremum point B is higher than the extremum point A.
2. The extremum point B is higher than the extremum point C.
3. The extremum point C is lower than the extremum point A.

The emergence of such elementary structure on any time frame is a definitive sign of the following upward correction in the same flow where the primitive fractal was formed. Here is an illustration to this case:

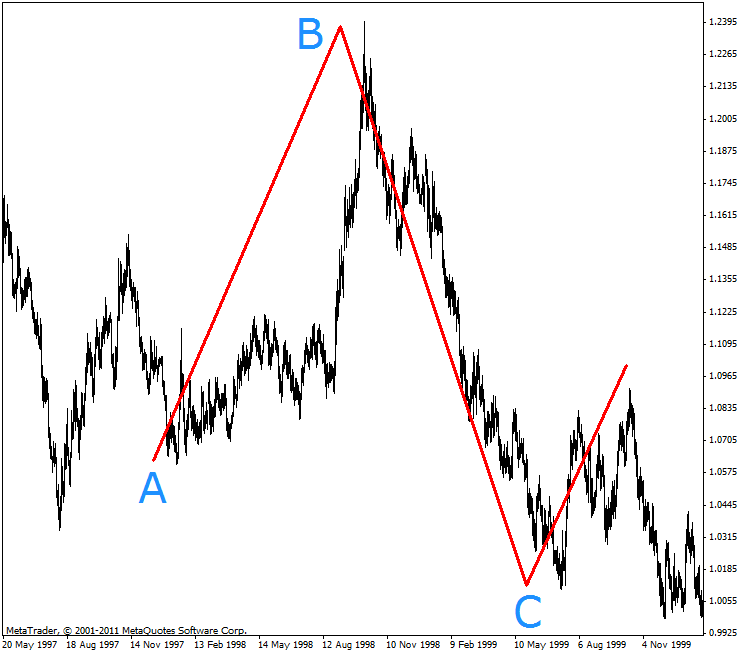
Figure 8. Downtrend correction

It is easy to see that the upward correction at hand has formed the fourth type of elementary fractals - downtrend pattern mirroring the earlier described fractal preceding the upward trend. Let us define the three key characteristics of the fourth primitive:

1. The extremum point B is lower than the extremum point A.
2. The extremum point B is lower than the extremum point C.
3. The extremum point C is lower than the extremum point A.

The emergence of such elementary structure on any time frame from М1 to MN1 is a clear indication of the downtrend following in the same flow where the primitive fractal was formed.

Just as in the case with the uptrend pattern but in an inverted form, unless and until the fluctuating price falls below the point B and goes beyond the boundaries of the formed primitive, the downtrend will be unconfirmed. There is also a similar rule.

Rule: a confirmed downtrend is followed by an upward correction in the same flow.

This rule leaves no alternative either - if there is a formed downtrend in the flow and such downtrend is confirmed, it can only be followed by an upward correction in the same flow, without exception.

This implies that any downtrend upon its confirmation forms the next pattern, an elementary structure of the primitive fractal preceding the upward correction. Regardless of the time the downtrend can last, it will sooner or later be followed by the upward correction.

The pattern description preceding the upward correction has already been provided above.

Visually, the fourth elementary fractal appears as shown below.

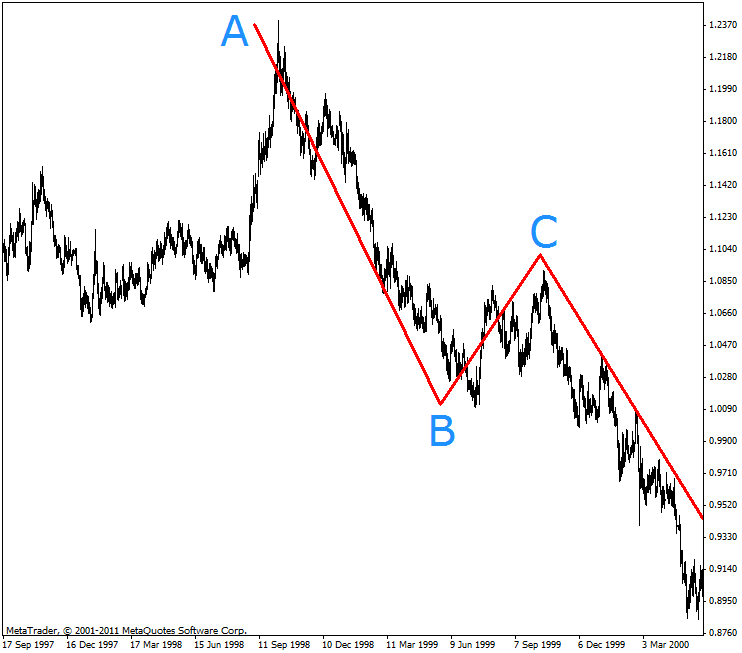
Figure 9. Downtrend

Let us sum it up. Any price movement on any time frame in the near future is explicitly determined by one of the four existing primitive fractals. The same four elementary patterns make up a structure of the entire set of fractals in the wave matrix.

A trend is always followed by an opposite correction. A correction may be followed by either a trend or another correction, such movement being in any case opposite to the preceding correction.

2.2. Driving force of the market

One way or another, the money flowing in and out of the market disturb the dynamic equilibrium of flows. The incoming waters make the river flow towards the "North Pole" - up along the price axis. The outflows - to the "South Pole", down along the price axis.

Despite the existence of general terms like "trend" and "correction", prices of financial instruments always follow a trend in a flow which is the main driving force of the market at any certain point of change in the delta of the price.

Rule: a trend is the main driving force in any market.

By structure and level of development, trends can be simple, extended and truncated. If a trend fails to make the price go outside the primitive fractal and remains unconfirmed until the counter-trend movement, such trend falls under the category of truncated trends. Truncated trends usually appear within corrections as well as structures forming the pattern of subsequent trends.

Wave patterns in Elliott Wave Principle also comprise a truncated trend pattern. Such pattern is called "Truncated5" and represents a truncated fifth impulse wave that does not move beyond the extremum of the third impulse wave.

In general, every confirmed trend is either simple or extended. Extended trends in the immediate short flow have a confirmed trend and make the price go 100% beyond the start, bringing it to 162% and higher.

Examples of such patterns in the context of the wave theory are "Extension1" being the first wave extension, "Extension3" being the third wave extension, "Extension5" being the fifth wave extension in impulses. The structure of a simple trend may be made up of both a trend and correction but simple trends are usually limited to the level of 100% of their start. Wave patterns can be illustrated by "Impulse" and "Impulse2", or more complex examples - "Diagonal1", "ExpTriangle5".

Rule: a correction shall have a trend at least at one iteration level of its structure.

Corrections often have quaint forms and a mixed structure. The wave theory defines a lot of corrective patterns however in terms of primitives, it is generally reasonable to group all corrective movements into simple and complex only.

The structure of a simple correction is made up of series of explicit trends, superior in number. The structure of a complex correction is made up of series of explicit corrections, superior in number. Nevertheless, every corrective movement in either case has a trend as a driving force deep in its structure. This driving force quite often brings corrective formations beyond the 100% retracement limit.

As a simple example, let us have a look at the primitive fractal representing a classic truncated trend that appeared in the main long flow. The resulting fractal (А-В-С) identified a downtrend. There were sharp oscillations in the trend over the course of its development causing the price to bounce off the standard Fibonacci retracements.

A regression model of the main flow showed the exhaustion of this trend after the next bounce of the price off 61.8% Fibonacci expansion level. The exhaustion occurred in the unconfirmed state of the trend - the point "В" has not been knocked down.

Such disposition suggests a clear counter-trend pattern - a primitive consisting of the points "В" and "С" and the bounce point off 61.8% level. Thus, the truncated trend formed a base, a platform for the subsequent uptrend within the given long flow.

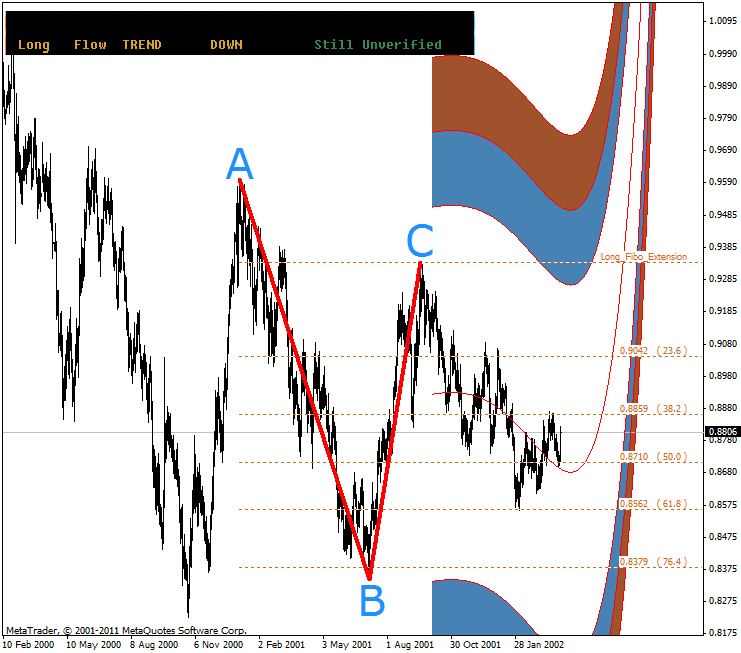
Figure 10. Uptrend base

The uptrend in the long flow was realized in the form of the extended trend, its structure being made up of series of consecutive trends in two short flows - the river was constantly increasing its volume due to two tributaries.

Earlier, when the price bounced off 61.8% Fibonacci expansion level, this pair of arms ensured the required outflow resulting in the completely formed and implemented model "truncated trend - extended trend" made up of two primitive fractals.

At the same time, this extended trend was the main driving force for the development of the first stage of the corrective movement in the long fractal structure that was followed by the second corrective stage on the whole completing the formation of the new primitive fractal as a base for the global trend of 2006-2008. A detailed analysis of the EURUSD exchange rate performed using the implemented software solution can be found on the official website of Stairway to Heaven LLC.

Conclusion

So, we have once again demonstrated the opportunities of MetaTrader 4 in the implementation of science-oriented projects and proposed a general idea of the fractal wave matrix and a new concept of market flows in the form of nonlinear wave regression channels.

The article material is generally intended for drawing the developers' attention to the covered aspects and peculiarities of a technical analysis and forecasting since the potential of this area of study is far from being exhausted. Stairway to Heaven LLC in their turn express their appreciation and gratitude to the MetaTrader 4 developers.