Ich muss eine Funktion mit beliebigen Einstellungen interpolieren, also habe ich Splines gewählt.
Ich verstehe richtig, dass ich unterschiedliche Interpolanten durch die Anzahl der Knotenpunkte erhalte, was kann ich sonst noch variieren?
Und die zweite Frage, was ist besser, für die Interpolation aus der Liste zu wählen, wenn ich nur viele verschiedene Interpolationen der ursprünglichen Serie (Variation ist wichtig) bauen müssen
Welche Wahl besser ist, ist eine sehr schwierige Frage. Ein Ansatz, die so genannte empirische Risikominimierung, wird in Wapnicks Buch Algorithms and Dependency Recovery Programs entwickelt. 1972, so scheint es.
Welches die bessere Wahl ist, ist eine sehr schwierige Frage. Ein Ansatz, die so genannte empirische Risikominimierung, wird in Wapnicks Buch "Algorithms and programs for dependence reconstruction" entwickelt. Es scheint 1972 zu sein.
Wahrscheinlichkeitsmaximierung/Minimierung des empirischen Risikos ist, so wie ich es verstehe, nur eine allgemeine Bezeichnung für die entsprechenden Algorithmen. Ich brauche nicht den Algorithmus selbst, sondern nur die Möglichkeit, Kurven zu modifizieren, vorzugsweise schnell und variabel, mit der Möglichkeit, Interpolationswerte an neuen Punkten zu finden (das Spline-Paket ermöglicht Letzteres).
Wahrscheinlichkeitsmaximierung/Minimierung des empirischen Risikos ist, so wie ich es verstehe, nur eine allgemeine Bezeichnung für die entsprechenden Algorithmen. Ich brauche nicht den Algorithmus selbst, sondern nur die Möglichkeit, Kurven zu modifizieren, vorzugsweise schnell und variabel, mit der Möglichkeit, Interpolationswerte an neuen Punkten zu finden (das Spline-Paket ermöglicht Letzteres)
Sowohl die Methode der maximalen Wahrscheinlichkeit als auch die Minimierung des Risikos (ich erinnere mich, nicht des empirischen, sondern des durchschnittlichen Risikos) sind keine Namen von Algorithmen, sondern von Methoden der Zielsetzung bei der Problemlösung. Wenn das Ziel erreichbar ist, führt es zu einem Algorithmus, der notwendigerweise mit dem Ziel übereinstimmt und eine Implementierung seiner Erreichung in bestimmten Fällen ist. Wenn man weder Ziele noch Algorithmen braucht, um sie zu erreichen, kann man keine Ratschläge für die Auswahl von Interpolationsfunktionen geben. Es bleibt Ihnen überlassen, so zu wählen, wie Ihr Herz es Ihnen sagt...
Ich muss eine Funktion mit beliebigen Einstellungen interpolieren, also habe ich Splines gewählt.
Ich verstehe richtig, dass ich unterschiedliche Interpolanten durch die Anzahl der Knotenpunkte erhalte, was kann ich sonst noch variieren?
Und die zweite Frage, was soll ich für die Interpolation aus der Liste auswählen, wenn ich nur viele verschiedene Interpolationen der Ausgangsreihe erstellen muss (Variabilität ist wichtig)?
Das Wertvollste für einen Händler ist nicht die Interpolation und nicht die Approximation, sondern die Extrapolation.
Splines sind für die Extrapolation nicht geeignet.
Ich habe große Erfahrung und Verständnis für polynomiale Approximation-Extrapolation. Weniger erfahren ist Fourier.
Die Extrapolation durch Polynom- und Fourier-Methoden ist von völlig unterschiedlicher Natur. Die Fourier-Extrapolation kann aufgrund ihres periodischen Charakters (diese Linie ist eine Summe von Sinuskurven unterschiedlicher Frequenz, Phase und Amplitude) nur auf den flachen Markt angewandt werden und neigt immer dazu, zurück zu gehen,während die polynomiale Extrapolation im Gegensatz dazu gut für den Trend ist, da sie aufgrund ihres Grades immer versucht, nach oben oder unten zu "fliegen".
Daher ist es sinnvoll, diese beiden Methoden zu kombinieren, um gute Extrapolationsergebnisse zu erzielen.
Die polynomiale Annäherung ist für Programmierer von besonderem Interesse, da diese Art der Annäherung sehr gut optimiert ist und sehr schnell berechnet werden kann. Es ist mir gelungen, aus den Zyklen zur Berechnung der Koeffizienten herauszukommen.
Es ist auch wichtig, daran zu denken, dass alle Arten der Annäherung mit jedem neuen Punkt neu zeichenbare Linien erzeugen. Nur der Taster der Näherungslinie wird nicht neu gezeichnet.
Eine polynomielle Näherung hat im Gegensatz zu einer Fourier-Näherung nur eine Lösung. Dies ermöglicht die Erstellung einzigartiger Folien, die nicht neu gezeichnet werden können:
Verstehe, zufällig zu raten ist auch nicht schlecht. Es hat also niemand ähnliche Probleme gelöst. Ich werde es mir vorstellen, ich werde es sehen.
Niemand hat es gelöst - falsch. Alle Interpolationsmethoden haben ihre theoretische Rechtfertigung und in der Regel ein klares Ziel. Zum Beispiel minimieren zwei kubische Defekte die potentielle Energie der elastischen Biegung eines Lineals, das durch die Nägel geht, die an den Knotenpunkten des Splines in das Brett geschlagen werden. Auf diese Weise wurde eine glatte Kurve (Fehler kleiner als 3) aus einer Tabelle von Punkten in einer Zeichnung mit einem Schiffsumriss oder einem Flügelprofil gewonnen. Die gleichen Splines stellen die Durchbiegung eines mehrstöckigen Balkens in elastischer Mathematik dar. Um die Ergebnisse der Interpolation mit unterschiedlichen Zielen zu vergleichen, benötigt man ein verallgemeinerndes Ziel, ein Kriterium, das für jede Interpolationsmethode berechenbar ist. Sie richtet sich nach der Anzahl der zu bestimmenden Koeffizienten. Grob gesagt, wenn eine Polynomapproximation mit einer Erhöhung des Polynomgrades von 3 auf 7 die Summe der Quadrate der Abweichung um 20 % reduziert, dann ist Grad 3 sinnvoller als 7. Das Analogon in der Funktechnik ist, wenn ich mich nicht irre, die Grenzfrequenz des Filters.
Das Wertvollste für einen Händler ist nicht die Interpolation oder Approximation, sondern die Extrapolation.
Splines sind für die Extrapolation nicht geeignet.
Ich habe große Erfahrung und Verständnis für polynomiale Approximation-Extrapolation. Weniger Erfahrung - Fourier.
Die Extrapolation durch Polynom- und Fourier-Methoden ist von völlig unterschiedlicher Natur. Die Fourier-Extrapolation kann aufgrund ihres periodischen Charakters (diese Linie ist eine Summe von Sinuskurven unterschiedlicher Frequenz, Phase und Amplitude) nur auf den flachen Markt angewandt werden und neigt immer dazu, zurück zu gehen,während die polynomiale Extrapolation im Gegensatz dazu gut für den Trend ist, da sie aufgrund ihres Grades immer versucht, nach oben oder unten zu "fliegen".
Daher ist es sinnvoll, diese beiden Methoden zu kombinieren, um gute Extrapolationsergebnisse zu erzielen.
Die Polynomnäherung ist für Programmierer von besonderem Interesse, da diese Art der Näherung sehr gut optimiert ist und sehr schnell berechnet werden kann. Es ist mir gelungen, aus den Zyklen zur Berechnung der Koeffizienten herauszukommen.
Es ist auch wichtig, daran zu denken, dass alle Arten der Annäherung mit jedem neuen Punkt neu zeichenbare Linien erzeugen. Nur der Taster der Näherungslinie wird nicht neu gezeichnet.
Eine polynomiale Näherung hat im Gegensatz zu einer Fourier-Näherung nur eine Lösung. Dies ermöglicht die Erstellung einzigartiger Folien, die nicht neu gezeichnet werden können:
Das ist in Ordnung. Ich habe nichts zu extrapolieren, es ist eine Interpolation erforderlich. Ich meine, dass es keinen Sinn macht, eine Prognose auf der Grundlage einer solchen Extrapolation zu erstellen. Es ist notwendig, dass diese Linie so stark wie möglich ist, von einer Seite zur anderen, wie Ihre blaue Linie. Und ich möchte in der Lage sein, eine Lösung für die neuen Punkte zu erhalten, ja (ohne Neuberechnung auf der Grundlage der bestehenden Formel).
Ich wollte nur wissen, was besser ist - Polynome, Splines oder andere Unterarten. Und vielleicht wäre der 10. Grad auch ganz lustig.
Niemand hat es gelöst - es ist falsch. Alle Interpolationsmethoden haben ihre theoretische Rechtfertigung und in der Regel ein klares Ziel. Zum Beispiel minimieren kubische Defekte an zwei Splines die potentielle Energie der elastischen Biegung eines Lineals, das durch Nägel läuft, die an den Knotenpunkten der Splines in das Brett geschlagen werden. Auf diese Weise wurde eine glatte Kurve (Fehler kleiner als 3) aus einer Tabelle von Punkten in einer Zeichnung mit einem Schiffsumriss oder einem Flügelprofil gewonnen. Die gleichen Splines stellen die Durchbiegung eines mehrstöckigen Balkens in der elastischen Mathematik dar. Um die Ergebnisse der Interpolation mit unterschiedlichen Zielen zu vergleichen, benötigt man ein verallgemeinerndes Ziel, ein Kriterium, das für jede Interpolationsmethode berechenbar ist. Sie richtet sich nach der Anzahl der zu bestimmenden Koeffizienten. Grob gesagt, wenn eine Polynomapproximation mit einer Erhöhung des Polynomgrades von 3 auf 7 die Summe der Quadrate der Abweichung um 20 % reduziert, dann ist Grad 3 sinnvoller als 7. Das Analogon in der Funktechnik ist, wenn ich mich nicht irre, die Grenzfrequenz des Filters.
Es ist nur so, dass, wenn ich versuche, alles zu erklären, was ich damit vorhabe, es wieder ein paar Seiten lang wird :) Sie brauchen Variabilität, unterschiedliche Polynomgrade, Anzahl der Gitterpunkte usw.
Das ist in Ordnung. Ich habe nichts zu extrapolieren, es ist eine Interpolation erforderlich. In dem Sinne, dass eine Prognose über eine solche Extrapolation im Nachhinein sinnlos ist. Es ist notwendig, dass diese Linie so stark wie möglich ist, von einer Seite zur anderen, wie Ihre blaue Linie. Und ich möchte in der Lage sein, eine Lösung für die neuen Punkte zu erhalten, ja (ohne Neuberechnung auf der Grundlage der bestehenden Formel).
Ich wollte nur wissen, was besser ist - Polynome, Splines oder andere Unterarten. Und vielleicht wäre der 10. Grad auch cool.
Genaue Interpolation? Sind Sie sicher? Keine Angleichung? Und ist sie nicht interpoliert?
Sie werden nicht jeden Tick interpolieren.
Wenn Sie eine Interpolation an Zwischenknoten (z. B. ZigZag-Knoten) ohne Neuzeichnen benötigen, kommt es darauf an, wo sich der nächste Knoten befindet.
Sie können ein nicht wiederholbares klares ZigZag nur erstellen, wenn Sie eine Zeitmaschine haben. Es gibt keine Möglichkeit, ohne eine Zeitmaschine festzustellen, dass der aktuelle Balken ein Extremwert ist.
Es gibt jemanden im Forum, den ich regelmäßig als "Pferdeschwanz-Redrawer" bezeichne.
Der springende Punkt ist der Pferdeschwanz.
Es ist ein Klassiker dieses Genres - die SMA um eine halbe Periode nach links zu verschieben und diese halben Perioden wie zufällig mit einem Polynom irgendeines Grades zu beenden. Zum Beispielhttps://www.mql5.com/ru/forum/224374. Sie haben es wahrscheinlich schon gesehen.
Sie können mit Splines eine sehr schöne Interpolation entlang von Zickzack-Extremen durchführen, aber Sie müssen sich darüber im Klaren sein, dass zwischen den letzten zwei oder drei Knoten eine erneute Zeichnung stattfinden wird. Ohne sie geht es nicht!
Wenn sie nicht neu gezeichnet wird, handelt es sich nicht um eine Interpolation, sondern um das, was ich eine Spur der Annäherungslinie nenne (keine Interpolation!).
Abgesehen von Polynomen sehe ich bis jetzt nichts Nachvollziehbares.
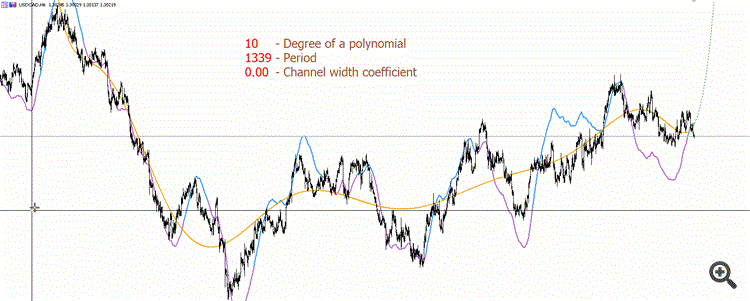
Hier ist ein speziell aufgenommenes gif, um ein Beispiel für ein Polynom höheren Grades (10) zu demonstrieren, um zu verstehen, wie viel weniger "schön" es ist, als ich möchte :))
Die violette und blaue Linie kann nicht neu gezeichnet werden. Violett ist das Polynom "nach unten", blau ist das Polynom "nach oben".
Außerdem ist die Genauigkeit nicht ausreichend, um Polynome hohen Grades zu berechnen. Wir werden spezielle Bibliotheken verwenden müssen, die Typen höherer Präzision verwenden. Die Tatsache, dass der "Tracer" bei kleinen Zeitabschnitten im gif zu "springen" beginnt - das ist der Grund, warum Double nicht präzise genug ist.
Ich persönlich sehe jedoch keinen praktischen Nutzen für Polynome vom Grad über 5.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Ich muss eine Funktion mit beliebigen Einstellungen interpolieren, also habe ich Splines gewählt.
Ich verstehe richtig, dass ich unterschiedliche Interpolanten durch die Anzahl der Knotenpunkte erhalte, was kann ich sonst noch variieren?
Und die zweite Frage, was ist besser, für die Interpolation aus der Liste zu wählen, wenn ich nur viele verschiedene Interpolationen der ursprünglichen Serie (Variation ist wichtig) bauen müssen