Von der Theorie zur Praxis - Seite 622

Neuer Kommentar
 
Es wäre cool, ein Team zu gründen ... wie das Produkt zu fördern, wie es zu schaffen, wie es zu testen und etwas Geld zu verdienen ... aber ist es mehr Spaß als diese Diskussion Club:)
 
Es ist wirklich wie eine Matrix, die jeder betrachtet, aber nicht sehen kann... alle Wohnungen und Trends haben einen Anfang und ein Ende. Ihr seid in der Matrix, Kameraden, sogar die Knöpfe: rot und blau, als ob Mobius es vorgeschrieben hätte) Ich schlage vor, wir kehren für weitere Diskussionen nach Zeon zurück))
 
Alexander_K2:

Kolmogorow ist ein klügerer Mann als die meisten, die auf den Bildschirm starren. Und seine Anforderungen an die BP-Vorhersage sind einfach: Erwartung = konstant und periodischer ACF.

Mit solchen Anforderungen kann jeder Narr vorhersagen, ganz zu schweigen von Kolmogorov)
 
Alexander_K2:

Und jetzt kommt das, was man sagen muss.

Wenn ich mir die inkrementellen Verteilungen ansehe und wie sie ihre statistischen Momente in Abhängigkeit von den Ableseintervallen der Notierungen verändern, wird mir klar, dass die Marktpreise NICHT die Eigenschaft der Selbstähnlichkeit haben. Diese Eigenschaft ist einzigartig für Prozesse mit stabilen, unendlich teilbaren (z. B. normalen) Verteilungen der Inkremente - wie die Brownsche Bewegung. Dies ist auf dem Markt nicht der Fall.

Offensichtlich haben Mandelbrot und seine Mitstreiter, die keine Ahnung von Physik haben (oder noch schlimmer - sie haben Ahnung, verheimlichen sie aber sorgfältig), die verzweifelten Menschen absichtlich getäuscht, damit sie auf Tickdaten und kleine Zeitrahmen setzen und sich durch den Verlust ihrer Einlagen die Taschen füllen.

Na also, geht doch!

Forschung über

http://tpq.io/p/rough_volatility_with_python.html

dieselbe https://hal.inria.fr/hal-01350915/document
rough_volatility_with_python
rough_volatility_with_python
  • tpq.io
The code in this iPython notebook used to be in R. I am very grateful to Yves Hilpisch and Michael Schwed for translating my R-code to Python. For slideshow functionality I use RISE by Damián Avila. $$ \newcommand{\beas}{\begin{eqnarray*}} \newcommand{\eeas}{\end{eqnarray*}} \newcommand{\bea}{\begin{eqnarray}} \newcommand{\eea}{\end{eqnarray}}...
 
Alexander_K2:

Und jetzt kommt das, was man sagen muss.

Wenn ich mir die inkrementellen Verteilungen ansehe und wie sie ihre statistischen Momente in Abhängigkeit von den Ableseintervallen der Notierungen verändern, wird mir klar, dass die Marktpreise NICHT die Eigenschaft der Selbstähnlichkeit haben. Diese Eigenschaft ist einzigartig für Prozesse mit stabilen, unendlich teilbaren (z. B. normalen) Verteilungen der Inkremente - wie die Brownsche Bewegung. Dies ist auf dem Markt nicht der Fall.

Offensichtlich haben Mandelbrot und seine Mitstreiter, die keine Ahnung von Physik haben (oder noch schlimmer - sie haben Ahnung, verheimlichen sie aber sorgfältig), die verzweifelten Menschen absichtlich getäuscht, damit sie auf Tickdaten und kleine Zeitrahmen setzen und sich durch den Verlust ihrer Einlagen die Taschen füllen.

Das war's!

Sie haben bereits Verschwörungstheorien ins Spiel gebracht... ein weiterer Haufen Mist.

Lesen Sie das Thema:

http://inis.jinr.ru/sl/vol2/Physics/Динамические%20системы%20и%20Хаос/Федер%20Е.,%20Фракталы,%201991.pdf

 
Igitt!
 

Nur um klarzustellen, was ich anstrebe.

Ich habe gerade begonnen, mit dem 60. Orderflow von Erlang zu arbeiten (Lesen von Tick-Kursen, im Durchschnitt einmal pro Minute).

Das folgende Histogramm zeigt z.B. die Steigerungen des Paares EURJPY:

Statistik:

Dies ist praktisch eine Laplace-Verteilung.

Die Summe der Zuwächse (~Preis) und die Zuwachsmodule (~Dispersion) sind bei einem relativ großen Probenumfang (ein Tag - für M1 oder eine Woche - für M5) eines solchen SP normalverteilt.

Das Ziel ist es also, zu einer reinen Laplace-Verteilung zu gelangen, dann haben wir wirklich ein direktes Analogon des Ornstein-Uhlenbeck-Prozesses mit einer Rückkehr zum Mittelwert.

 
In 600 Seiten hat der Kommandant nie verstanden, dass die Rückkehr zum Durchschnitt nicht von der Form der Inkremente abhängt)
 

Ich würde auch gerne raten, welche Abschnitte der Geschichte er für seine Charts verwendet, es gibt Trendabschnitte für mehrere Monate, und es gibt Seitwärtsbewegungen

Ebenso wie das Prinzip des "Springens" von M1 nach M5 nicht klar ist, braucht er Konsistenz oder zumindest eine Rechtfertigung. Er wäre dort mit solchen Talenten von unschätzbarem Wert, sie addieren auch erfolgreich Monate, dann Quartale, dann Saisons = die Ausgabe der richtigen statistischen Daten

)))

 
Alexander_K2:

Nur um zu verdeutlichen, was ich anstrebe.

Ich habe gerade begonnen, mit dem 60. Orderflow von Erlang zu arbeiten (Lesen von Tick-Kursen, im Durchschnitt einmal pro Minute).

Das folgende Histogramm zeigt z.B. die Steigerungen des Paares EURJPY:

Statistik:

Dies ist praktisch eine Laplace-Verteilung.

Die Summe der Zuwächse (~Preis) und die Zuwachsmodule (~Dispersion) sind bei einem relativ großen Probenumfang (ein Tag - für M1 oder eine Woche - für M5) eines solchen SP normalverteilt.

Das Ziel ist es also, zu einer reinen Laplace-Verteilung zu gelangen, dann haben wir wirklich ein direktes Analogon des Ornstein-Uhlenbeck-Prozesses mit einer Rückkehr zum Mittelwert.

Im Allgemeinen sehe ich, dass die Kurtosis reduziert wird, die Schwänze werden aufgefangen ---> von Laplace zu normal, von normal zu gleichmäßig. Was steht dann am Anfang? Nicht Laplace? Warum? Weil es sich leicht durch einen Exponenten beschreiben lässt, wenn man eine Seite nimmt.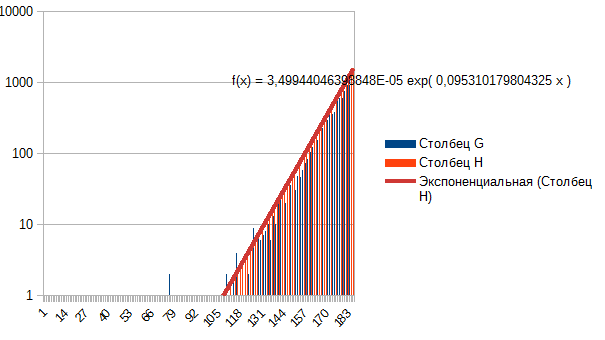 Dies ist das EURUSD-Minuten-Monatsfenster.


1...615616617618619620621622623624625626627628629...1981
Neuer Kommentar