Hallo zusammen...
Ich habe eine Frage zur Fourier-Transformation...
Nach Fourier-Transformation und Hochpassfilterung mit Rücktransformation,
Ich muss die Berechnung der resultierenden Funktion außerhalb des Bereichs der Transformation fortsetzen (wenn Sie ein Beispiel nennen können)...
Es muss nichts weiter berechnet werden, da die Fourier-Transformation nur auf periodische Funktionen angewendet wird.
Nehmen wir an, wir haben ein periodisches Signal in dem erhaltenen Bereich,
Dies hat zur Folge, dass der Anfang der Reihe eine Fortsetzung der periodischen Folge ist... Oder?
Nehmen wir an, wir haben ein periodisches Signal in dem erhaltenen Bereich,
Dies hat zur Folge, dass der Anfang der Reihe eine Fortsetzung der periodischen Folge ist... >> richtig?
Welche Art von Array?
Die Fourier-Transformation wird für die approximierte Periode von 0 bis 2 * PI durchgeführt.
2*PI ist 0 Grad für die nächste Periode, für die die Annäherung bereits für die vorhergehende Periode durchgeführt wurde.
Dann schauen wir uns die Zahl an...
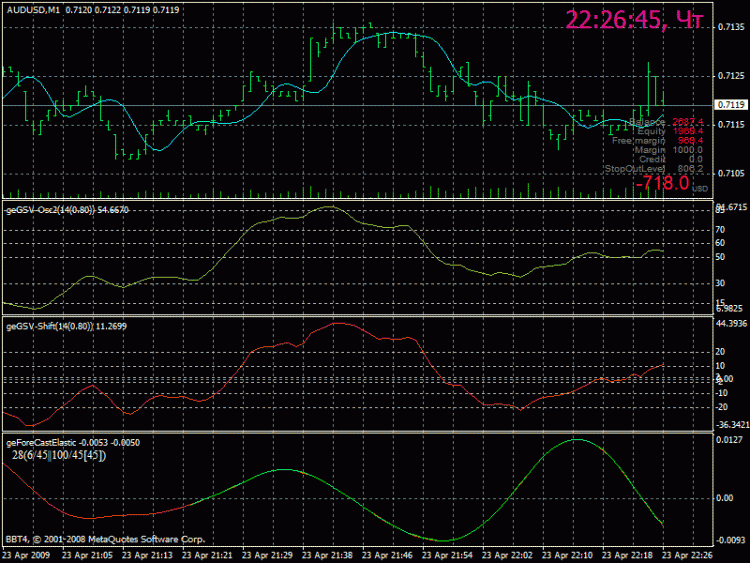
Die Kurve (rot) in der unteren Anzeige ist die grüne Linie, die bei der Umrechnung mit den folgenden Parametern erhalten wurde
die Größe des Konvertierungsfensters 2^6=64 Punkte, die Anzahl der verwendeten Frequenzen beträgt 45.
d.h. wir erhalten einen Anschein der resultierenden Kurve ... die wir dem Original aufgezwungen haben ...
Wie Sie aus der Abbildung ersehen können, ist die Ersetzung des Anfangs durch das Ende kein echtes Ergebnis -
Die Frage ist also, wie die Kurve, die durch die grüne Linie dargestellt wird, fortgesetzt werden kann...
....
Die Frage ist also, wie die Bewegung der durch die grüne Linie dargestellten Kurve fortgesetzt werden kann...
Das ist der Trick bei Fourier- und ähnlichen Transformationen!
Sie bringen zunächst die Nicht-Stationarität des Marktes in eine quasi-stationäre Form, zumindest...
Dann können Sie alles in stationäre Sinuswellen umwandeln und damit weitermachen, wo Sie wollen. Aber... Sie werden wahrscheinlich nicht weiterkommen...
Vielleicht sollten wir die Frage dann anders formulieren...
Wie kann die in der Abbildung dargestellte Funktion so angenähert werden, dass die Kurve in einem kleinen Abschnitt fortgesetzt werden kann?
Vielleicht sollten wir die Frage dann anders formulieren...
Wie lässt sich die in der Abbildung gezeigte Funktion am besten annähern, so dass die Kurve auf einer kleinen Fläche fortgesetzt werden kann?
In einem kleinen Gebiet kann jede beliebige Näherungsmethode verwendet werden, um damit zu extrapolieren.
Ich verwende den Lagrangianer.
Dann schauen wir uns die Zahl an...
Die Kurve (rot) in der unteren Anzeige ist die grüne Linie, die bei der Umrechnung mit den folgenden Parametern erhalten wurde
die Größe des Konvertierungsfensters 2^6=64 Punkte, die Anzahl der verwendeten Frequenzen beträgt 45.
d.h. wir erhalten einen Anschein der resultierenden Kurve ... die wir dem Original aufgezwungen haben ...
Wie Sie aus der Abbildung ersehen können, ist die Ersetzung des Anfangs durch das Ende kein echtes Ergebnis -
Die Frage ist also, wie die Bewegung der durch die grüne Linie dargestellten Kurve fortgesetzt werden kann...
1. Warum in aller Welt haben Sie beschlossen, dass die 64 Punkte, die für die Annäherung genommen werden, eine periodische Funktion sind?
2. Die Anzahl der Oberschwingungen darf die Hälfte der genommenen Proben nicht überschreiten, d. h. bei einer Annäherung durch 64 Teilungen der Periode beträgt die maximale Oberschwingung 31.
3. unrealistisches Ergebnis, weil Sie eine nichtperiodische Funktion für die Annäherung verwendet haben und daher die Periodenfortsetzung nicht übereinstimmt. Es wurde Ihnen bereits gesagt, dass PF nur bei periodischen Funktionen wirksam ist, alles andere ist ein Tamburinspiel.
Sie sollten zwei identische Zeiträume nehmen: 0 - 2*PI, 2*PI - 4*PI. Verwenden Sie beide zur Erzeugung von PF und vergleichen Sie, ob die Amplituden und Phasen der Oberwellen übereinstimmen. Ist dies nicht der Fall, bedeutet dies, dass die Funktion nicht periodisch ist und die Abtastperiode entweder verlängert oder verkürzt werden sollte (Verkleinerung oder Vergrößerung - dies dient dazu, die Phasenverschiebungen für einzelne Oberschwingungen zu betrachten).
Alles andere ist nur Tanzen mit Tamburin.
Es sind zwei identische Zeiträume zu nehmen: 0 - 2*PI, 2*PI - 4*PI. Bei beiden ist es notwendig, PF zu biegen und zu vergleichen, ob die Amplituden und Phasen der Oberwellen übereinstimmen. Wenn nein, dann bedeutet dies, dass die Funktion nicht periodisch ist und die Abtastperiode entweder erhöht oder verringert werden muss (Verringerung oder Erhöhung hängt von den Phasenverschiebungen der einzelnen Oberschwingungen ab)
Im Prinzip ist dies auch ein "Tamburintanz", nur mit mehr "Aufwand". Das Ergebnis wird eine "schönere" Geschichte sein - mehr nicht.
Periodisch ist eine Funktion, für die es T gibt, so dass für jedes x die folgende Gleichheit f(x) = f(x+T) gilt. Dann ist T die Periode der Funktion f(x).
Einfach ausgedrückt: Der Händler hat keine Garantie dafür, dass bei der Wahl von T nach dem vorgeschlagenen Algorithmus (als gemeinsames Vielfaches von zwei aufeinanderfolgenden Zeiträumen) der dritte Zeitraum desselben Stichprobenumfangs dem gewählten Wert entspricht (und der dritte Zeitraum ist nur der Zeitraum, für den die Extrapolation durchgeführt wird). Bei keinem Algorithmus zur Auswahl von T gibt es eine Garantie.
Und übrigens - wenn die Funktion periodisch ist, wozu brauchen wir dann diesen Fourier? Hat noch nie jemand darüber nachgedacht? Finden Sie einen Punkt und ersetzen Sie einfach die Werte, das ist alles ;). Das heißt natürlich, wenn Sie die Zeit gefunden haben und nicht mit dem Tamburin tanzen....
>> Viel Glück dabei.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Hallo zusammen...
Ich habe eine Frage zur Fourier-Transformation...
Nach Fourier-Transformation und Hochpassfilterung mit Rücktransformation,
Sie wollen die Berechnung der resultierenden Funktion außerhalb des Bereichs der Transformation fortsetzen (wenn Sie ein Beispiel nennen können)...