似乎你必须使方程相等,然后对它们进行微分(这个问题让人想起救护车,当你可以在田野里以低速走捷径,或者在沥青上以较高的速度行驶,但路线较长--在什么时候你要离开沥青进入田野?)
那么问题来了,你是如何编造它们的呢?到目前为止,它只以迭代的形式工作。
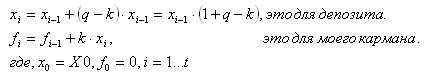
我们需要以分析形式(作为对时间t 的函数依赖)提出。
进一步扩展f的公式,即把它变成fi=fi(x0)。
啊哈!然后它变成了这样。
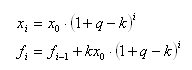
而在t个月的时间内提取的资金量的表达式可以写成:。
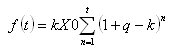
如果是这样,那就更好了。下一步是什么?你必须要摆脱量...
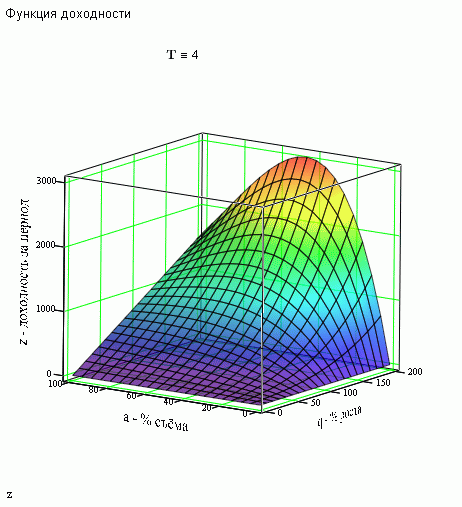
将看起来像这样。
不可能!...
你能说得更具体些吗?我是说以公式的形式。
因此,你可以真正看到去除率方面的最佳效果!
其中q是GP的分母,b1是第一项
alsu:
回顾几何级数的n个首项之和的公式
Shaitan!事实上,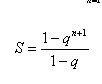 。
。
那么最后,提取的资金之和的表达式将被给出:。
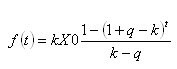
剩下的就是取时间导数并将其等同于零......。是的。
Neutron:
很明显,要提取的金额是q,而且只在t期结束时提取。在所有其他情况下,提取的金额将减少。
大家好!
我已被允许使用X0 卢布的存款,时间为 T 个月。每个月的存款都会得到当前存款价值 X 的固定百分比q。我被允许每个月从账户中提取一些百分比k,但不超过 q 的价值。
因此,问题是在t 个月的时间内最大限度地提取资金的数量。
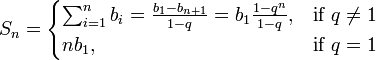
大家好!
我已被允许使用X0 卢布的存款,时间为 T 个月。每个月,存款 X 的当前价值的固定百分比q 被存入。我被允许每个月从账户中提取百分比k,但不超过 q 的价值。
因此,任务是在t 个月的时间内最大限度地提取资金。似乎很明显,每月提取全部应计利息q 并不是最好的选择,因为在这种情况下,存款不会增长,而且由于账户上的负载较少,最终提取的金额可能更大......另一方面,k 的值不应该归零,因为在这种情况下,提取的资金量也会归零。显然,真相是在中间的某个地方。但具体在哪里?
请帮助我以一般方式分析解决这个问题。
P.S. 没有在与贸易无关的zadacha 分支发帖,因为提议的主题与后者有关。