租用者 - 页 19

新评论
 

Sorento:

В чём другое? Ведь требуется строго больше. :)

好吧，上帝保佑，严格来说是这样的。我同意。

 
Neutron:


用你的方法估算，并给我结果。

我在图中给出了条件{N=120，q(mo)=60.91%/12初始资本=100}，而摆弄K是我无能为力的。

如果有人能给我这些条件的kOpt--我将把考虑到四舍五入的postnumerand列表...

;)

 

所以，现在有一个问题要问Matemat 和Sorento：上面，你们两个人都提到了独特的米哈伊尔-安德烈耶维奇 的决定，即--那么现在呢，一切都很清楚......喜欢 - 下一步是什么？

事实证明，尊敬的米哈伊尔-安德烈耶维奇 除了对翻倍的时间有一个减少的公式，什么都没有:-)我想，一般来说，我们要等待Alexey 对 kOpt 的近似解。

 
Neutron:

所以，现在有一个问题要问Matemat和Sorento：上面，你们两个人都提到了独特的米哈伊尔-安德烈耶维奇 的决定，即--那么现在呢，一切都很清楚......喜欢 - 下一步是什么？

事实证明，尊敬的米哈伊尔-安德烈耶维奇 除了对翻倍的时间有一个减少的公式外，什么都没有:-)所以，我想我们要等待Alexey 对 kOpt 的近似解决方案。

有趣的结论。

涉及任何（包括比例）在截止日期前提款的策略Topt- 不是最佳的...假设Depo比Topt长--当然。

请看图片（数字）...

;)

 

似乎我们正在开始解决一个稍微不同的（更复杂的）问题。

让我提醒你，根据规定，我有一笔使用时间为 t 的存款，在此基础上每月产生当前存款额的恒定利息q ，我必须每月提取固定利息k，不超过q， 不低于0%。就这样了。

我必须找到这样的 kOpt ，在不考虑存款的情况下，在t 期实现最大的提款。这个解决方案必须以分析形式提出，作为两个参数q和 t 的函数（数值解决方案，以各种图表和依赖关系的形式的部分解决方案没有兴趣，因为它们已经得到了）。如果分析解是近似的，那么必须指定q和 t 的极限值，在这个极限值中，问题解的宣称精度是可以达到的。

P.S. 所有的计谋，如通货膨胀、应计利息q 的非恒定性、参数k 的变化等等，我认为在得到最简单情况的解决方案之前，没有必要考虑。

 

"回顾一下，按照惯例，我有一个使用时间为 t 的存款，在此基础上每月累积当前存款额的恒定百分比q ，我必须每月提取一个不超过q和 不低于0%的固定百分比k。就是这样。"

.

谢尔盖，而且问题已经有了答案，虽然公式不是太简单，但也很好理解。这种情况下的答案通常在参考书中以提名图的形式给出。

从问题的说明中我们可以看到："q位于0.1<q<0.3的范围内"。

指定 "时间t " 的范围

 

奥列格，对于外汇交易t 可以设置为50。少一点是没有意义的，因为在存款的特征寿命 小于5年的情况下，提取所有的利润是正确的，而最初的存款规模应该提供 "终身 "的利息。如果生活时间超过5年，那么初始存款规模不是问题，你可以从1000卢布开始，但出现了最佳提款比例。此外，如果我们考虑到特征寿命对执行来说不是强制性的（因为我们说的是统计学），我们可以从公式中排除这个参数，使其等于常数=50。因此，我们对kOpt 的分析近似值（理想情况下）只来自一个参数--TC的平均熟练度--q。

kOpt=q for t<50

kOpt=F(q) for t>50

在指定的条件下，分析依赖性F(q)的近似形式是我们想要找出的。

 

我还不知道如何使这个公式变得简单。牛顿方法 至少在第三次或第四次迭代时就能得到一个或多或少的精确解。事实证明，这是一个非常繁琐的、多层次的公式。

现在对q的 澄清进一步证实了二项式展开在这里是无用的：即使在q=0.1和t=10 的情况下，你也必须保留太多的二项式条款。而t 和q 越大，情况就越糟糕。换句话说，对于合理的t（可能不低于20）几乎总是

(1+q-k)^t ~ exp((q-k)t)

观察表明，在大q 和小t（例如，分别为0.3和10）的情况下，提取我一个月所赚的大部分（70%）是最理想的。

在小q 和小t 的情况下，在合理的范围内没有极值：有必要提取你所有的收入。

同时，在中等q值 和中等t 值（0.2和20）的情况下，提取自己收入的一半中的很大一部分（44%）是合理的。

那么，在中等q 和大t（0.2和30）的情况下，提取较小部分的收入（26%）是合理的。

诸如此类，不一而足。在不同的参数下，该问题的表现有质的不同。似乎没有一个乐观的、单一的答案。也许可以尝试根据q 和t 对k 做出某种估计？

P.S. 我看到了你的评论，谢尔盖。好的，修复t=50。问题变得简单了：只需提取一小部分收益（q=0.1，t=50-->k/q=0.3，即30%）。这是可能的最大k/q。

 

..................

.................

................

阿尔法的最佳值对应于从正区到负区的过渡。

.

上面已经给出了公式，我在这里重复一下

你可以在Matcadet中重现它---你可以快速调整参数。

(而B并没有发挥作用）。

 
Mathemat:

也许可以尝试对k 作为q 和t 的函数进行某种估计？


那么就失去了分析解决方案的优雅性。在这种情况下，使用数值解法是比较正确的。这个问题对于简单的表达来说似乎是遥不可及的...

我试图简化提款之和的原始表达式 。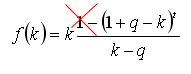

在这种情况下，参数 k 上的一阶导数的一般形式被大大简化，变成了一个简单的二次方程。

.

通过求解，我们可以得到一个近似的表达，即

在 t>50，q>0.1的范围内具有可接受的准确性

我想要更多...

1...121314151617181920212223242526...31
新评论