租用者 - 页 20 1...131415161718192021222324252627...31 新评论 [删除] 2011.02.27 13:44 #191 . 那就更方便了。 Neutron 2011.02.27 13:46 #192 avtomat: 你可以马上在Matcadet中重现它------你就可以快速调整参数。 稍后。你需要搬进去。 [删除] 2011.02.27 13:48 #193 以防万一。 eps=ln(1+q) Sceptic Philozoff 2011.02.27 14:05 #194 我没有看到阿尔法的明显表达,奥列格。你说它已经在那里了。但在这里你有一个等于k 上的导数的函数,中子 早就计算过了。 2 中子: 好,现在一切都更简单了。固定t=50,寻找实验中对 q 的依赖α = k/q。它是平滑和直接的,易于近似。我们将该近似值作为第一近似值,用于...切线法,并在第一步停止。让我们试试吧。 [删除] 2011.02.27 14:12 #195 Mathemat: 我没有看到阿尔法的明确表达,奥列格。你说它已经在那里了。但你在这里得到的是一个等于对k 的导数的函数,这是中子 早就计算过的。 并且没有α的明确表达, 。 在这样的情况下,工程实践中使用了各种类型的提名图。 . 呃...我是不是错过了什么...那个早就计算好的正确公式在哪里呢? Sceptic Philozoff 2011.02.27 14:21 #196 https://www.mql5.com/ru/forum/131914/page2-中子 在该页的第二个帖子。这与要解决的关于k 的方程是一样的。而你的指数,奥列格,只是一个变相的阶梯函数,因为xi是一个对数......。 总之,稍后,希望我能够发布t=50 在q=0.1...0.3时的分析解决方案。 [删除] 2011.02.27 14:39 #197 Mathemat: https://www.mql5.com/ru/forum/131914/page2-中子 在该页的第二个帖子。这与要解决的关于k 的方程是一样的。而你的指数,奥列格,只是一个变相的阶梯函数,因为xi是一个对数......。 总之,稍后我希望能发布q=0.1...0.3时t=50 的分析解决方案。 你认为这是同一件事吗...? . 嗯......除了可能有一点拉伸....。 Sceptic Philozoff 2011.02.27 14:41 #198 奥列格,你把它弄混了。中子 在该页的第二个 帖子。这里是方程式。 将t=36 和q=0.3代入左边的函数,并将其建立为k 的函数。 [删除] 2011.02.27 14:43 #199 Mathemat: 奥列格,你把它弄混了。中子 在该页的第二个 帖子。这里是方程式。 好了...你不喜欢我的解决方案的什么? Sceptic Philozoff 2011.02.27 14:49 #200 是的,这是很正常的 "解决方案",但有点矫揉造作,而且用ATS的术语过多。此外,它已经在这个主题的第二页上得到了。 这不是一个解决方案,而只是一个需要找到其零点的函数。我们一直试图根据这个功能找到这个零点,已经有很长一段时间了。 你不是说把二维码转换为代数方程类可以帮助解决这个问题吗?但到目前为止,你只得到了我们要找的那个函数的零。如果你认为你比中子"更合理 "地得到了同样的结果--说明原因。 在函数的 "简单 "推导中,我们不需要将 "格子 "函数翻译成连续时间,因为我们根本没有这样的问题。但你做到了!但你的 "解决方案 "有什么优势呢? 1...131415161718192021222324252627...31 新评论 您错过了交易机会: 免费交易应用程序 8,000+信号可供复制 探索金融市场的经济新闻 注册 登录 拉丁字符(不带空格) 密码将被发送至该邮箱 发生错误 使用 Google 登录 您同意网站政策和使用条款 如果您没有帐号,请注册 可以使用cookies登录MQL5.com网站。 请在您的浏览器中启用必要的设置,否则您将无法登录。 忘记您的登录名/密码? 使用 Google 登录
.
那就更方便了。
你可以马上在Matcadet中重现它------你就可以快速调整参数。
稍后。你需要搬进去。
以防万一。
eps=ln(1+q)
我没有看到阿尔法的明显表达,奥列格。你说它已经在那里了。但在这里你有一个等于k 上的导数的函数,中子 早就计算过了。
2 中子: 好,现在一切都更简单了。固定t=50,寻找实验中对 q 的依赖α = k/q。它是平滑和直接的,易于近似。我们将该近似值作为第一近似值,用于...切线法,并在第一步停止。让我们试试吧。
我没有看到阿尔法的明确表达,奥列格。你说它已经在那里了。但你在这里得到的是一个等于对k 的导数的函数,这是中子 早就计算过的。
并且没有α的明确表达,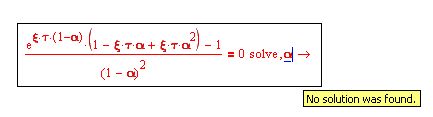 。
。
在这样的情况下,工程实践中使用了各种类型的提名图。
.
呃...我是不是错过了什么...那个早就计算好的正确公式在哪里呢?
https://www.mql5.com/ru/forum/131914/page2-中子 在该页的第二个帖子。这与要解决的关于k 的方程是一样的。而你的指数,奥列格,只是一个变相的阶梯函数,因为xi是一个对数......。
总之,稍后,希望我能够发布t=50 在q=0.1...0.3时的分析解决方案。
https://www.mql5.com/ru/forum/131914/page2-中子 在该页的第二个帖子。这与要解决的关于k 的方程是一样的。而你的指数,奥列格,只是一个变相的阶梯函数,因为xi是一个对数......。
总之,稍后我希望能发布q=0.1...0.3时t=50 的分析解决方案。
你认为这是同一件事吗...?
.
嗯......除了可能有一点拉伸....。
奥列格,你把它弄混了。中子 在该页的第二个 帖子。这里是方程式。
将t=36 和q=0.3代入左边的函数,并将其建立为k 的函数。
奥列格,你把它弄混了。中子 在该页的第二个 帖子。这里是方程式。
是的,这是很正常的 "解决方案",但有点矫揉造作,而且用ATS的术语过多。此外,它已经在这个主题的第二页上得到了。
这不是一个解决方案,而只是一个需要找到其零点的函数。我们一直试图根据这个功能找到这个零点,已经有很长一段时间了。
你不是说把二维码转换为代数方程类可以帮助解决这个问题吗?但到目前为止,你只得到了我们要找的那个函数的零。如果你认为你比中子"更合理 "地得到了同样的结果--说明原因。
在函数的 "简单 "推导中,我们不需要将 "格子 "函数翻译成连续时间,因为我们根本没有这样的问题。但你做到了!但你的 "解决方案 "有什么优势呢?