[存档!]纯数学、物理学、化学等:与贸易没有任何关系的大脑训练问题 - 页 614 1...607608609610611612613614615616617618619620621...628 新评论 [删除] 2012.07.04 12:45 #6131 Mathemat: 迪马,你为什么想知道与1相差千分之一的概率?如果你想要保证,那就没有了。诺贝尔奖获得者(LTCM)和尼德霍夫本人躲在概率后面,在一定程度上减一--仍然 "打"。 按千分之一的比例--没有必要。但120个交易是很多的,应该可以计算出少量的交易,例如--20、30、40。而30%对120来说是不够的。 而非常小的概率(非常大)被用来计算系统的大致寿命。重要的是要知道它将持续多长时间--一年或十年。 有什么可以依靠的吗?数学是最好的方法。 Sceptic Philozoff 2012.07.04 13:05 #6132 好吧,至少读一读一些基本的terw,反正会很方便的。 [删除] 2012.07.04 13:08 #6133 GaryKa, Mathemat 对吗? Sceptic Philozoff 2012.07.04 13:23 #6134 DmitriyN: 对吗? 这就对了! 但四舍五入的误差会吞噬所有的精确度。最好是从0到30的总和来计算。它将等同于你想知道的概率的加法。 GaryKa 2012.07.04 13:27 #6135 如果有球返回,那么总是p=q,所以我们可以简化右边的公式(*p^120)。 Sceptic Philozoff 2012.07.04 13:29 #6136 Mislaid: 我们从根本上解决这个问题:没有平等。确 定立方体面上的数字集不应该重叠。 有的情况下,有的情况下,面数之和等于17。 例如,(333332)>(662111),获胜的概率为23/36 ~ 0.64。的确,那里并不简单:(662111)并没有以任何明显的优势获胜。 似乎到目前为止,18个面孔的总和是最肥沃的。 Sceptic Philozoff 2012.07.04 13:47 #6137 GaryKa: 如果我们返回球,那么总是p=q,所以我们可以简化右边的公式(*p^120)。 我们回不回来其实并不重要。我们提取的东西太少,无法产生任何影响。但它可以被体面地简化。而在括号中的幂数,乘数(1/2)^120将保留。 嘿嘿。 2 迪马:不要去管这些组合。掌握正态分布,从零到对应于你的30的下限取一个定积分。在这个公式中,你会犯一个很大的错误,除非你找到一个简单组合之和的分析公式。 或者尝试从0到30的组合之和,P级不会困扰你。你可能会很幸运。 P.S. 简而言之,这很容易。看这里。 你需要计算k1,k2,然后计算积分。 取k1=0,k2=30,这样更准确。n=120,p=q=1/2。那么 (k2-np)/sqrt(npq) = (30-60)/sqrt(120*1/2*1/2) ~ -5.477 (k1-np)/sqrt(npq) = (0-60)/sqrt(120*1/2*1/2) ~ -10.954。 另外1/sqrt(2*pi)~0.39894也很方便。 将前两个数字代入积分极限,并将0.39894*exp(-x^2/2)代入积分函数,我们得到(这里 有一个关于取某些积分的服务)。 2.163*10^(-8). 所以你的概率是1-2.163*10^(-8) ~ 0.99999998。 甚至不要试图取积分下的函数的初始值:它是非整数。 [Archive!] Pure mathematics, physics, 用 MQL5 表示统计概率分布 多层感知器和反向传播算法(第二部分):利用 Python 实现并与 MQL5 GaryKa 2012.07.04 14:22 #6138 Mathemat: ...计算出正态分布...除非你能找到一个简单的组合之和的分析公式 ... 你的这些话给了我一个有趣的想法,试图找到一个通过正态分布计算组合的分析公式 )) [删除] 2012.07.04 14:25 #6139 Mathemat: 我会努力想办法的。好的链接。 Sceptic Philozoff 2012.07.04 14:41 #6140 GaryKa: 你的这些话给了我一个有趣的想法--试图找到一个通过正态分布计算组合的分析公式 )) 好吧,这就是本地的莫布-拉普拉斯 定理。 1...607608609610611612613614615616617618619620621...628 新评论 您错过了交易机会: 免费交易应用程序 8,000+信号可供复制 探索金融市场的经济新闻 注册 登录 拉丁字符(不带空格) 密码将被发送至该邮箱 发生错误 使用 Google 登录 您同意网站政策和使用条款 如果您没有帐号,请注册 可以使用cookies登录MQL5.com网站。 请在您的浏览器中启用必要的设置,否则您将无法登录。 忘记您的登录名/密码? 使用 Google 登录
迪马,你为什么想知道与1相差千分之一的概率?如果你想要保证,那就没有了。诺贝尔奖获得者(LTCM)和尼德霍夫本人躲在概率后面,在一定程度上减一--仍然 "打"。
而非常小的概率(非常大)被用来计算系统的大致寿命。重要的是要知道它将持续多长时间--一年或十年。
有什么可以依靠的吗?数学是最好的方法。
对吗?
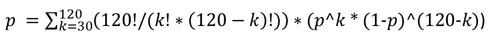
这就对了!
但四舍五入的误差会吞噬所有的精确度。最好是从0到30的总和来计算。它将等同于你想知道的概率的加法。
有的情况下,有的情况下,面数之和等于17。
例如,(333332)>(662111),获胜的概率为23/36 ~ 0.64。的确,那里并不简单:(662111)并没有以任何明显的优势获胜。
似乎到目前为止,18个面孔的总和是最肥沃的。
如果我们返回球,那么总是p=q,所以我们可以简化右边的公式(*p^120)。
我们回不回来其实并不重要。我们提取的东西太少,无法产生任何影响。但它可以被体面地简化。而在括号中的幂数,乘数(1/2)^120将保留。
嘿嘿。
2 迪马:不要去管这些组合。掌握正态分布,从零到对应于你的30的下限取一个定积分。在这个公式中,你会犯一个很大的错误,除非你找到一个简单组合之和的分析公式。
或者尝试从0到30的组合之和,P级不会困扰你。你可能会很幸运。
P.S. 简而言之,这很容易。看这里。
你需要计算k1,k2,然后计算积分。
取k1=0,k2=30,这样更准确。n=120,p=q=1/2。那么
(k2-np)/sqrt(npq) = (30-60)/sqrt(120*1/2*1/2) ~ -5.477
(k1-np)/sqrt(npq) = (0-60)/sqrt(120*1/2*1/2) ~ -10.954。
另外1/sqrt(2*pi)~0.39894也很方便。
将前两个数字代入积分极限,并将0.39894*exp(-x^2/2)代入积分函数,我们得到(这里 有一个关于取某些积分的服务)。
2.163*10^(-8).
所以你的概率是1-2.163*10^(-8) ~ 0.99999998。
甚至不要试图取积分下的函数的初始值:它是非整数。