[存档!]纯数学、物理学、化学等:与贸易没有任何关系的大脑训练问题 - 页 304 1...297298299300301302303304305306307308309310311...628 新评论 Sceptic Philozoff 2010.03.23 20:48 #3031 设F(x,y)=min( x, y + 1/x, 1/y ),则 F(1/y, 1/x) = min( 1/y, 1/x + y, x ) = F(x,y)。 因此,如果你用1/x替换y,用1/y替换x,最小值不会改变。Y=1/x。 所以F(x,1/x) = min( x, 2/x, x ) = min( x, 2/x )。如果x<sqrt(2),它等于x,否则等于2/x。 画出两条曲线y=x和y=2/x。很明显,最大值正好在它们的交点上,并且等于sqrt(2)。 问题书中的解决方案相当含糊,我不喜欢它。 下一个(8日)。 这一部分的构造是很微妙的。让我们把阴谋论抛在脑后。 问题的第二部分(也是第八部分)。 随机谐振 MQL5 中的范畴论 (第 5 神经网络变得简单(第 68 部分):离线优先引导政策优化 Sceptic Philozoff 2010.03.23 23:36 #3032 另一个后续行动是几何(8日)。 richie 2010.03.24 17:46 #3033 简化后的数字。 Sceptic Philozoff 2010.03.24 17:48 #3034 里奇,阴影三角形中怎么会有相等的角? richie 2010.03.24 17:50 #3035 Mathemat писал(а)>> 里奇,阴影三角形中怎么会有相等的角? 在中央的那个?这很明显。 Sceptic Philozoff 2010.03.24 17:53 #3036 那么,请继续吧。证明一下吧。 顺便说一下,问题陈述中并没有说原始三角形是等边的。尽管它被画成了一个等边的。 richie 2010.03.24 17:54 #3037 Mathemat писал(а)>> 来吧。证明一下吧。 我还没有想出办法。我会考虑的。 - 好吧,无论如何,这个想法是这样的。 4x三角形的面积等于大三角形 和4个小三角形面积之差的三分之一,也就是4平方厘米。 要找到大三角形 的面积,你需要找到它的边(在图中是A)。 按面积求中心三角形 的边,知道它是等边的不是问题,它等于sqr(4*S/sqr(3))。 михаил потапыч 2010.03.24 17:55 #3038 Richie >>: В центральном? Это очевидно. 只有当三个三角形(除中心三角形外)是相同的时候 但根据条件,这并不是一个事实 Sceptic Philozoff 2010.03.24 18:02 #3039 这不是一个事实。 必须有一些东西可以坚持下去。有一条线索,但我还不知道该如何处理它。 richie 2010.03.24 18:32 #3040 Mischek писал(а)>> 只有当三个三角形(除了中心的那个)是相同的时候 但这并不是一个事实。 好吧,你让我完全糊涂了。 我以为这个大三角形是等边的。小的3个三角形是等边的,因此,它们是相似的。 1...297298299300301302303304305306307308309310311...628 新评论 您错过了交易机会: 免费交易应用程序 8,000+信号可供复制 探索金融市场的经济新闻 注册 登录 拉丁字符(不带空格) 密码将被发送至该邮箱 发生错误 使用 Google 登录 您同意网站政策和使用条款 如果您没有帐号,请注册 可以使用cookies登录MQL5.com网站。 请在您的浏览器中启用必要的设置,否则您将无法登录。 忘记您的登录名/密码? 使用 Google 登录
F(1/y, 1/x) = min( 1/y, 1/x + y, x ) = F(x,y)。
因此,如果你用1/x替换y,用1/y替换x,最小值不会改变。Y=1/x。
所以F(x,1/x) = min( x, 2/x, x ) = min( x, 2/x )。如果x<sqrt(2),它等于x,否则等于2/x。
画出两条曲线y=x和y=2/x。很明显,最大值正好在它们的交点上,并且等于sqrt(2)。
问题书中的解决方案相当含糊,我不喜欢它。
下一个(8日)。
这一部分的构造是很微妙的。让我们把阴谋论抛在脑后。
问题的第二部分(也是第八部分)。
简化后的数字。
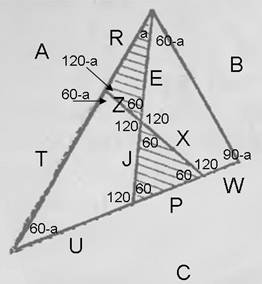
里奇,阴影三角形中怎么会有相等的角?
顺便说一下,问题陈述中并没有说原始三角形是等边的。尽管它被画成了一个等边的。
来吧。证明一下吧。
-
好吧,无论如何,这个想法是这样的。
4x三角形的面积等于大三角形 和4个小三角形面积之差的三分之一,也就是4平方厘米。
要找到大三角形 的面积,你需要找到它的边(在图中是A)。
按面积求中心三角形 的边,知道它是等边的不是问题,它等于sqr(4*S/sqr(3))。
В центральном? Это очевидно.
只有当三个三角形(除中心三角形外)是相同的时候但根据条件,这并不是一个事实
必须有一些东西可以坚持下去。有一条线索,但我还不知道该如何处理它。
只有当三个三角形(除了中心的那个)是相同的时候
但这并不是一个事实。
好吧,你让我完全糊涂了。
我以为这个大三角形是等边的。小的3个三角形是等边的,因此,它们是相似的。