Sultonov'un regresyon modeli (RMS) - pazarın matematiksel bir modeliymiş gibi davranmak.
ana kalıpları tanımlayan kalıpları arayın
Korelasyon ve regresyon teorisinin tüm ana hükümleri, incelenen verilerin normal dağılımı varsayımına dayanarak geliştirilmiştir. Girdi parametreleriniz (fiyat) normal bir dağılıma sahip mi?
anlamadım
Prensip olarak, RMS'nin zaman serisi (TS) dahil olmak üzere bir dizi rakama gömülü herhangi bir deseni ortaya çıkardığını göstereceğim, sanırım, bu sayıların dizideki görünümünün doğasına bakılmaksızın. Tüm bunlar ve diğer incelikler, rastgele bir serinin analizi de dahil olmak üzere belirli örnekler üzerinde tartışılacaktır.
RMS daha sonra gerçek veya hayali bir model bulacaktır, ancak normal dağılımın olmaması nedeniyle modelin tahmin değeri 0 olacaktır. Bunlar incelikler değil, temel budur.
Tam olarak neyi anlamadın?
RMS daha sonra gerçek veya hayali bir model bulacaktır, ancak normal dağılımın olmaması nedeniyle modelin tahmin değeri 0 olacaktır. Bunlar incelikler değil, temel budur.
RMS, en uygun bağımlılığı değil, en uygun olanı bulacaktır. Ve ilk verilerin dağılımının normalliğinin yokluğu veya varlığı hakkında, ayrı bir tartışma dalı açalım ve bu vakfın bilenlerinin burada paralel konuşmasına izin verelim.
Anlaşıldı ..... Ve haklı olarak - evet, o, normallik! Sadece yoluna girer
PS, modelin tahmin değeri 0'a yakın olacak
Doğrusal bir fonksiyonla başlayalım.
Serinin Yi = a+bxi sayılarıyla verildiğini hayal edin:
xi Yi
0.00000001 10.0000
1.00000001 15.0000
2.000000001 20.0000
3.00000001 25.0000
4.00000001 30.0000
5.00000001 35.0000
6.00000001 40.0000
7.00000001 45.0000
8.00000001 50.0000
9.00000001 55.0000
10.00000001 60.0000
11.00000001 65.0000
120000001 70.0000
13.0000001 75.0000
14.00000001 80.0000
15.00000001 85.0000
16.00000001 90.0000
17.00000001 95.0000
18.00000001 100.0000
İşte gerçek ve hesaplanmış değerlerin bir grafiği, model hatası 2.78163E-14%: 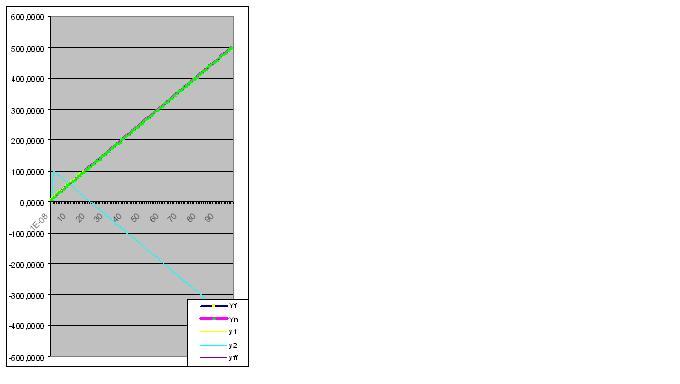
Anlaşıldı ..... Ve haklı olarak - evet, o, normallik! Sadece yoluna girer
PS, modelin tahmin değeri 0'a yakın olacak
Kalıcılığınız nedeniyle, Y=tg(0.1x)+2 işlevini analiz etme örneğini kullanarak modelin tahmin yeteneklerini göstererek başlamak zorundayım ve ilk 8 basamak çiftini giriyorum:
xi Yi
0,00000001 2,0000
1.00000001 2.1003
2000000001 2.2027
3.00000001 2.3093
4.0000001 2.4228
5.00000001 2.5463
6.00000001 2.6841
7.00000001 2.8423
Hata %0.427140953: 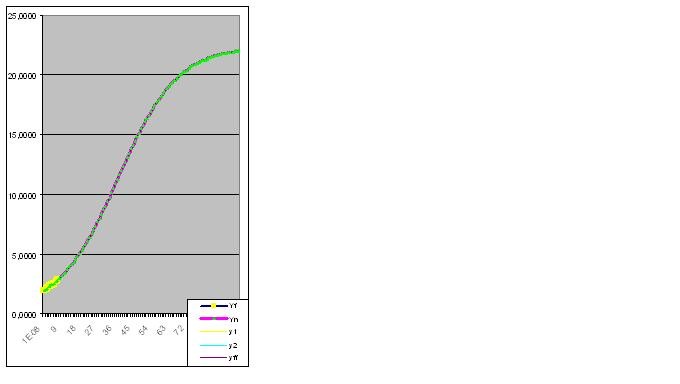
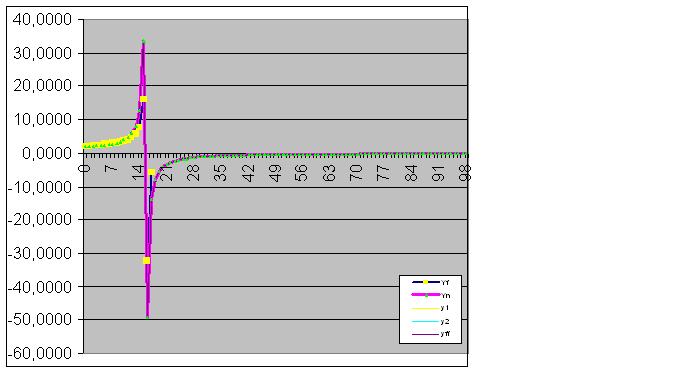
Bununla birlikte, model, nesnenin gelecekteki "garip" davranışını hemen tahmin ettiğinden, 9. basamak çiftini girmeye değer:
Verilerin daha fazla tanıtılması, "anomali" tahminini orijinal verilere yaklaştırır:
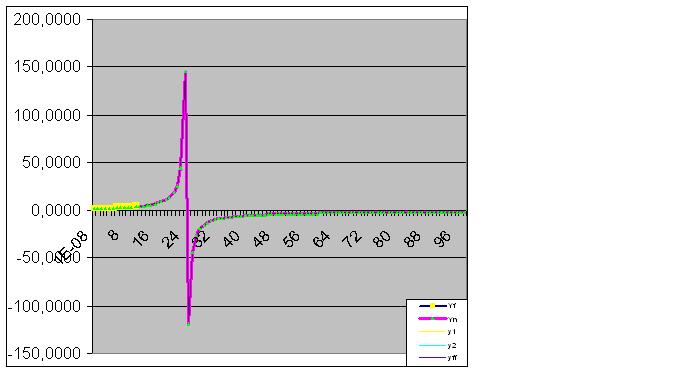
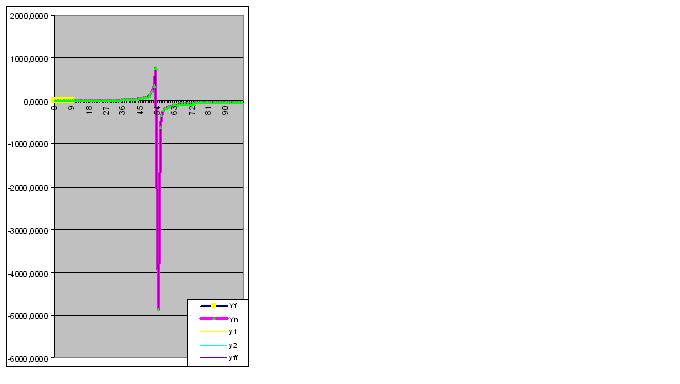
Böylece ilk veriler de öngörülen "aldatmacayı" gerçekleştirmeye başladı:
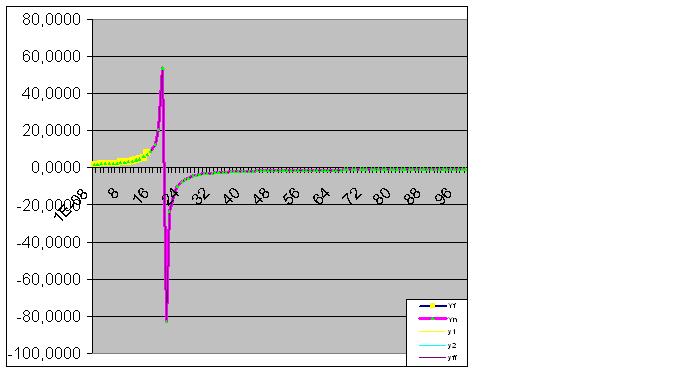
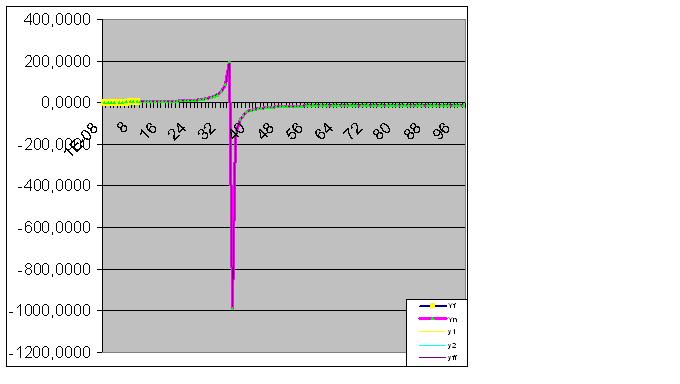
Ve nihayet, tahmin mükemmel bir şekilde gerçekleşti:
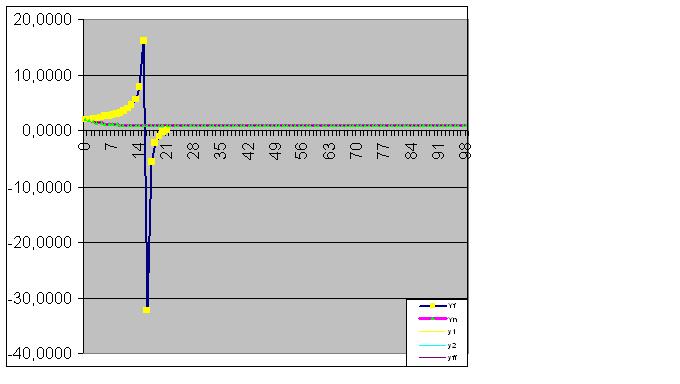
Ayrıca, model ideal olarak nesnenin son durumunu yakalar, böylece fonksiyonun gerçek değerlerinin toplamı, bilgisayar doğruluğu ile RMS'ye göre hesaplanana eşittir.
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz
Sevgili forum kullanıcıları, bu bir sır değil. ilgili olan, piyasanın ana kalıplarını tanımlayan bağımlılıkları bulma sorunudur. Burada, katılımcıların bu konudaki çeşitli önerileri ve bu noktaya kadar çeşitli kaynaklardan biriken teorik ve pratik materyal dahil olmak üzere mevcut tüm analiz araçlarıyla bu sorunun çözümüne yaklaşmaya çalışacağız. Bu çalışmanın sonucunda, bu işlevin şekli üzerinde bile duracak olursak, zaman ve emeğin boşa gitmediğini düşüneceğimizi düşünüyorum.
İyi bilinen kalıpları tanımlamanın basit örneklerini kullanarak RMS'nin yeteneklerini göstererek başlayacağım: doğrusal bağımlılık, parabol, hiperbol, üstel, sinüs, kosinüs, tanjant, kotanjant ve bunların kombinasyonları, kuşkusuz mevcut olan kombinasyonları. Market. Gerektiğinde yapıcı öneriler ve sağlıklı eleştirilerle bu dürtüde bana destek olmanızı rica ediyorum.