"Piyasa Fiyat Tahmini için Evrensel Regresyon Modeli" makalesi için tartışma - sayfa 8

Yeni yorum
 
yosuf:
Özel mesaj yoluyla iletişime geçin, koşullar hakkında bilgi edinin.
Göstergeler ücretli mi?
 
lyvel:
Добрый день, уважаемый Юсуфходжа, подскажите, где можно скачать индикаторы и советники о которых вы говорите?
Опубликован в кодбазе, пользуйтесь на здоровье!
 
joo:
Göstergeler ücretli falan mı? Kod tabanında yayınlandı, gönlünüzce kullanın!
 
Rosh:

Yeni makale Universal Regression Model for Market Price Prediction yayınlandı:

Yazar: Юсуфходжа

Güzel makale.

çok etkileyici

 
Olağanüstü !!! Bilginize katkıda bulunduğunuz ve ticaretimizi geliştirmek için büyük bir kalbe sahip olduğunuz için çok teşekkür ederiz.
 

Yazık ama makalenin en başında hatalar var.

İlk olarak, bir t zamanındaki fiyat artışının elbette bir değeri olacaktır ve bunu D0 ile gösteriyoruz. Varsayalım.

Sonra... Şimdi t=0'da fiyat üzerinde bir etki olmadığını anlıyorum ve görünüşe göre dış etkiden kaynaklanan bir fiyat artışı da yok. Ancak, deltaya yine D0 adını verdik.

Sonra dt/tau'yu zaten 1/C^2 olan formüle koyduk, yani geometrik gerilemeyi zaten hareket ettirecek olan etkiye ivme verdik. Neden yapalım? Sonuçta, bu etkinin ne olduğunu henüz tanımlamadık...

genel olarak.

 
new-rena:

Yazık ama makalenin en başında hatalar var.

İlk olarak, bir t zamanındaki fiyat artışının elbette bir değeri olacaktır ve bunu D0 ile gösteriyoruz. Varsayalım.

Sonra... Şimdi t=0'da fiyat üzerinde bir etki olmadığını anlıyorum ve görünüşe göre dış etkiden kaynaklanan bir fiyat artışı da yok. Ancak, deltaya yine D0 adını verdik.

Sonra dt/tau'yu zaten 1/C^2 olan formüle koyduk, yani geometrik gerilemeyi zaten hareket ettirecek olan etkiye ivme verdik. Neden yapalım? Sonuçta, bu etkinin ne olduğunu henüz tanımlamadık...

Peki, genel olarak...

1. Do fiyat artışı değil, t=0 zamanında fiyatı etkileyen kuvvetin başlangıç potansiyelidir.

2. Makaleden: ".... dengede olan piyasa fiyatının yalnızca, büyüklüğünü ve değerini fiyatla aynı boyutta ölçeceğimiz bazı dış kuvvetlerin D(t) etkisi altında değişebileceğini varsayalım.

Ayrıca, bu kuvvetin etkisinin başlangıcından itibaren t zamanının geçmesiyle piyasa fiyatındaki P(t) değişiminin, henüz bilmediğimiz bir düzenlilikle sıfır değerinden sürekli artarak, sonsuzda P(∞) = D0 değerine ulaşma eğiliminde olduğunu varsayalım. Yani, D0 ile bu etki gücünün niteliğine ve işaretine bağlı olarak piyasa fiyatında sonlu bir artış veya düşüşü kastediyoruz.

Ayrıca, D(t=0) = D0 olduğunu varsayıyoruz. Ayrıca, dt sonsuz küçük zaman dilimi boyunca, etkileyen kuvvetin t zaman anına kadar kalan D(t) kuvvetiyle orantılı olarak dD(t) değeri kadar azalacağını varsayalım:


Buradan, D(t)'nin t zamanına üstel bağımlılığını şu şekilde elde ederiz:

(1)

Nerede?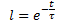

t - zaman serisi birimlerinde dengesizleştirici kuvvetin etkisinin başlangıcından itibaren geçen süre, saniye (dakika, saat, gün, hafta, on yıl, ay, yıl);

τ (tau) - orantılılık katsayısı, sayısal olarak sürecin zaman sabitine eşittir, sn.(dk, saat, gün, hafta, on yıl, ay, yıl)."

1/s^2'nin boyutsallığını nereden buldunuz? Bu oranın boyutsallığı yoktur. Ben bunu araya sıkıştırmadım, bir sürece etki eden kuvvetin değişim (azalma) oranının, kuvvetin kendisiyle orantılı olduğu hipotezini kurdum, ki bu mantıkla çelişmez, ve sonra bu hipotez tamamen doğrulandı. Bir orantılılık katsayısı olarak ve zamanın tersi olan a (alfa) = 1/tau oranını ortaya koydu. A (alfa) ile sistemin empedansını, yani sistemin sürecin akışına karşı direncini anlıyorum ve tau, daha sonra ortaya çıktığı gibi Laplace dönüşümlerinde zamanın görüntüsüdür ve sürecin analizini diferansiyel alandan sıradan olana götürmeye izin verir. Bu, herhangi bir sürecin bizimkinden farklı kendi zamanı olduğu ve tau'nun zamanların bir "çevirmeni" olarak hareket ettiği anlamına gelir. Makalenin girişinde tau'yu tahmin etmenin bir yolunu vermiştim:

Şimdi, eğer f fonksiyonunun t zamanının ilgili anlarındaki değerleri biliniyorsa, bu denklemden n, τ parametreleri ve β katsayısı aşağıdaki gibi belirlenir:

(12)

(13)

(14)

burada:

t ve t zamanının karşılık gelen anlarına ait f fonksiyonunun değerleri, aralığın ortasına atıfta bulunan sayısal farklılaştırma ile istikrarsızlaşmasının başlangıcından itibaren h0, h1,..., һk zaman anlarına ait P0, P1,..., Pk piyasa fiyatının gerçek değerleri tarafından belirlenir:

f1 = (P1 - P0)/(ch1 - ch0); f2 = (P2 - P1)/( ch2- ch1); f3 = (P3 - P2)/( ch3- ch2); ve böyle devam eder;

t1 = (ch0 + ch1)/2; t2 = (ch1 + ch2)/2; t3 = (ch3 + ch2)/2; vb.

12345678
Yeni yorum