Принципы реализации пакетной нормализации

Авторы метода предложили следующий алгоритм проведения нормализации. Вначале по выборке данных считаем среднее значение.

где:

• μB — среднее арифметическое признака по выборке;
• m — размер выборки (batch).

Затем считаем дисперсию исходной выборки.

Далее нормализуем данные выборки, приведя выборку к нулевому среднему и единичной дисперсии.

Обратите внимание, что в знаменателе к дисперсии выборки прибавляется константа ε — небольшое положительное число с целью исключить деление на ноль.

Но как оказалось, такая нормализация может исказить влияние исходных данных. Поэтому авторы метода добавили еще один шаг — масштабирование и смещение. Были введены переменные γ и β, которые обучаются вместе с нейронной сетью методом градиентного спуска.

Применение данного метода позволяет на каждом шаге обучения получать выборку данных с одинаковым распределением, что на практике делает обучение нейронной сети более стабильным и позволяет увеличить коэффициент обучения. В целом это позволит повысить качество обучения при меньших затратах времени на обучение нейронной сети.

Но в тоже время возрастают затраты на хранение дополнительных коэффициентов. Кроме того, для расчета скользящих средних и дисперсии требуется дополнительное выделение памяти на хранение исторических данных каждого нейрона на весь размер пакета. Тут можно посмотреть в сторону экспоненциальной средней. Для расчета EMA достаточно предыдущего значения функции и текущего элемента последовательности.

На рисунке ниже наглядно представлены графики скользящей средней и скользящей дисперсии на 100 элементов в сравнении с экспоненциальной скользящей средней и экспоненциальной скользящей дисперсии на те же 100 элементов. График был построен для 1000 случайных элементов из диапазона от -1,0 до 1,0.

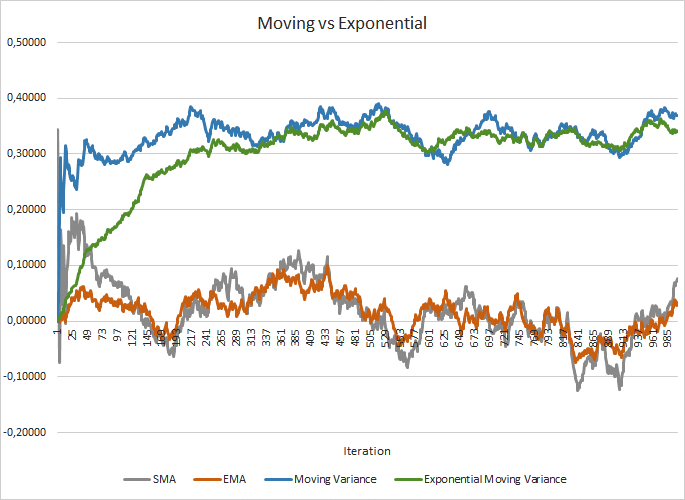
Сравнение графиков скользящей и экспоненциальной средних

Как видно на графике, скользящая средняя и экспоненциальная скользящая средняя сближаются после 120-130 итераций и дальше есть минимальное отклонение, которым можно пренебречь. К тому же график экспоненциальной скользящей средней имеет более сглаженный вид. А вот для расчета EMA достаточно предыдущего значения функции и текущего элемента последовательности. Напомню формулу экспоненциальной скользящей средней.

где:

• μi — экспоненциальное среднее признака по выборке на i-том шаге;
• m — размер выборки (batch);
• xi — текущее значение показателя.

Для сближения графиков скользящей дисперсии и экспоненциальной скользящей дисперсии потребовалось чуть больше итераций (310–320), но в целом картина похожая. В случае с дисперсией применение экспоненциальной средней дает не только экономию памяти, но и значительно снижает количество вычислений, т.к. для скользящей дисперсии мы бы пересчитывали отклонение от средней для всего пакета исторических данных.

На мой взгляд, использование подобного решения значительно снижает использование ресурсов памяти и затраты времени на проведение математических операций на каждой итерации прямого прохода.