Имеем систему уравнений
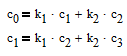
Из второго уравнения определим первый коэффициент
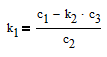
Подставим в первое уравнение
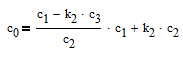
Отсюда определим второй коэффициент
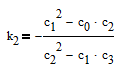
.
Вот и всё.
Два неизвестных коэффициента, два уравнения --- дают точное решение. Это основы линейной алгебры.Тогда что? Тогда никаких проблем посчитать систему уравнений любого размера, без всяких многоэтажных выводов - матрицей.
Потом усреднить коэффициенты и посчитать прогноз.
Тогда что? Тогда никаких проблем посчитать систему уравнений любого размера, без всяких многоэтажных выводов - матрицей.
не проблема, но количество уравнений в системе должно быть не менее кол-ва неизвестных параметров, принцип тот же , что и школьное уравнение:
x + y = 10
2x-y = 8
2 неизвестные - 2 уравнения = решение есть
Тогда что? Тогда никаких проблем посчитать систему уравнений любого размера, без всяких многоэтажных выводов - матрицей.
Потом усреднить коэффициенты и посчитать прогноз.
А я это хрен знает когда говорил. Матричные функции в Экселе - работают очень шустро.
Но, Юсуфу кажется, что решение с помощью формул из отдельных ячеек - работает быстрее, вдобавок если "усовершенствовать метод решения", и получить однопроходный алгоритм.
На самом деле - все эти задачи давно имеют типовые методы решения, и необходимо сосредоточить усилия не на попытке "обогнать" матричные расчеты, а на оценке пригодности выведенной аппроксимации для моделирования будущего хода цены.
не проблема, но количество уравнений в системе должно быть не менее кол-ва неизвестных параметров, принцип тот же , что и школьное уравнение:
x + y = 10
2x-y = 8
2 неизвестные - 2 уравнения = решение есть
Нет, там чуть сложнее. Через ранги, определители...
Скажем, для простейшего случая:
x + y = 10
2x + 2y = 8
Решения нет.
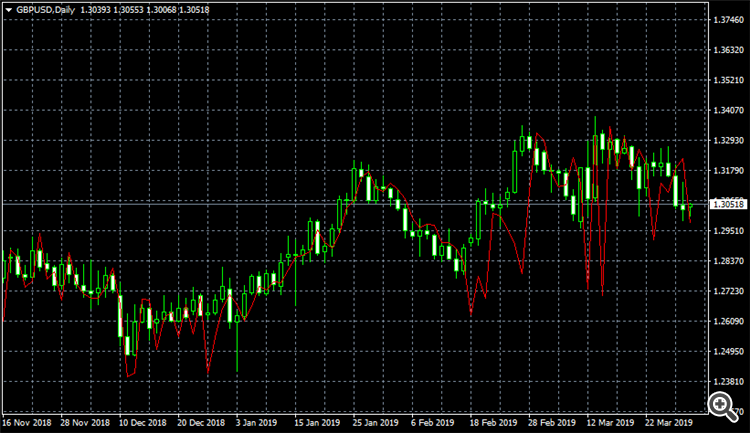
Вот что получилось по двум барам:
Красная линия это прогноз цены закрытия на момент открытия бара, по мере формирования бара не меняется.
Иногда линию не слабо мотает:
#property copyright "*" #property link "*" #property version "1.00" #property strict #property indicator_chart_window #property indicator_buffers 1 #property indicator_plots 1 #property indicator_label1 "Прогноз" #property indicator_type1 DRAW_LINE #property indicator_color1 clrRed #property indicator_style1 STYLE_SOLID #property indicator_width1 1 extern int SmPeriod = 14; double bk1[]; double bk2[]; double bsk1[]; double bsk2[]; double f[]; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit(){ IndicatorBuffers(5); SetIndexBuffer(0,f); SetIndexBuffer(1,bsk1); SetIndexBuffer(2,bsk2); SetIndexBuffer(3,bk1); SetIndexBuffer(4,bk2); return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]){ int limit=rates_total-prev_calculated; if(prev_calculated==0){ limit--; limit-=4; } for(int i=limit;i>=0;i--){ bk1[i]=k1(close[i],close[i+1],close[i+2],close[i+3]); bk2[i]=k2(close[i],close[i+1],close[i+2],close[i+3]); } for(int i=limit;i>=0;i--){ bsk1[i]=iMAOnArray(bk1,0,SmPeriod,0,0,i); bsk2[i]=iMAOnArray(bk2,0,SmPeriod,0,0,i); //f[i]=bsk1[i]*close[i+1]+bsk2[i]*close[i+2]; // проверка - линия проходит по close (при SmPeriod=1) f[i]=bsk1[i+1]*close[i+1]+bsk2[i+1]*close[i+2]; // прогноз } return(rates_total); } double k1(double c0,double c1,double c2,double c3){ return (c0/c2 - c1/c3)/(c1/c2 - c2/c3); } double k2(double c0,double c1,double c2,double c3){ return (c0/c1 - c1/c2)/(c2/c1 - c3/c2); }
Индикатор для МТ4 (придет модератор и перенесет тему, ну и ладно)
Что ж ты не довёл до ума...
Вот это у тебя неверно:
double k1(double c0,double c1,double c2,double c3){ return (c0/c2 - c1/c3)/(c1/c2 - c2/c3); } double k2(double c0,double c1,double c2,double c3){ return (c0/c1 - c1/c2)/(c2/c1 - c3/c2);
Имеем выражения для коэффициентов
![]()
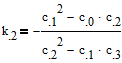
Делаем подстановку
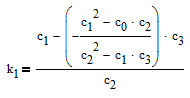
Упростим его
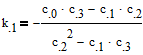
Теперь оба коэффициента выражены через известные величины.
Окончательно имеем:
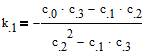
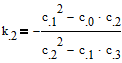
И не потеряй минусы перед дробями.
Смотрите в коде закомментированную строку:
/ проверка - линия проходит по close (при SmPeriod=1)
Это вычисление c0 на основе с1, с2 и полученных коэффициентов - проходит точно по ценам close, что подтверждает праивильность моего расчета коэффициентов.
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования

Все начинается здесь: https://www.mql5.com/ru/forum/307935.
Там в самом начале формула: Ц5 = Ц0 + а1Ц1 + а2Ц2 + а3Ц3 +а4Ц4
Потом переотсыл куда-то туда (а там картинка, якобы с выводом, но по факту в выводе откуда ушли, туда и пришли): https://www.mql5.com/ru/forum/86249/page3#comment_2520504
Короче, имеем систему из четырех уравнений. Давайте пока усложнять не будем и попробуем решить систему из двух уравнений:
c0 = k1*c1 + k2*c2
c1 = k1*c2 + k2*c3
с - это цена (допустим, цена закрытия), с0 - на нулевом баре, с1 - на первом и т.д. k1, k2 - коэффициенты которые надо найти.
Нерешаемость (за исключением редчайших случаев) сей системы, в том виде как она записана, не должна вызывать сомнений. Поэтому надо найти приближенное решение. Для этого от правой части отнимем левую:
k1*c1 + k2*c2 - c0 -> 0
k1*c2 + k2*c3 - c1 -> 0
Возведем в квадрат, что бы знак отклонения не мешал
(k1*c1 + k2*c2 - c0)^2 -> 0
(k1*c2 + k2*c3 - c1)^2 -> 0
Теперь найдем производные по k1 и к2, в итоге, как ни крути, получается:
2*c1*c2=0
Коэффициенты исчезли. Задача бы решалась, если бы полином был степенным (и это имело бы название "Полиноминальная регрессия").
Что не так в моей математике? Там же уже в воздухе витает мысль, что задача решаема, и даже как будто решение выкладывалсь в файле экселя... но... легенда есть легенда, уже нет этого файла (с объяснением веской причины, почему его уже нет).
Так что не так в моей математике? Решаема эта система уравнений или нет:
c0 = k1*c1 + k2*c2
c1 = k1*c2 + k2*c3