![]()
Получается то же самое. Это только другая форма записи, в маткадовской портянке ЕМА описана так же. Благодарю, значит с весами в портянке ошибки нет.
Сначала комент по преобразованиям
(1) Вас не смущает такие тестовые выводы по вашей формуле
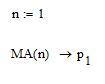 и
и 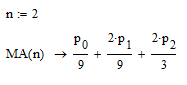
Явное расхождение между количеством членов цВР и количеством весовых коэффициентов. Похоже напутали с индексами. Ниже свой вариант
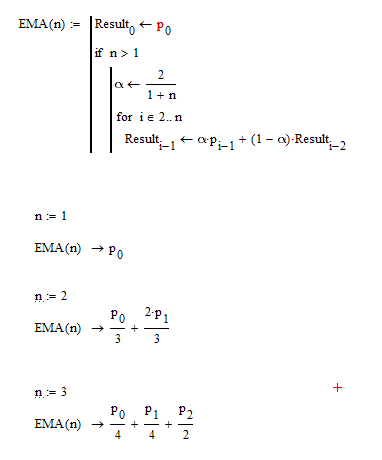
(2) Откуда вы вывели формулу F(n,x) (" разложение этой рекурсии в ряд " )
P.S. Я с EMA не работал, могу ошибаться, проверяйте
По замеру времени вычисления с помощью GetTickCount() на таких малых промежутках времени ничего не скажу. По моему это одна из тех фич что делает нашу жизнь ... веселее )
А вот это заинтересовало
А вот это заинтересовало
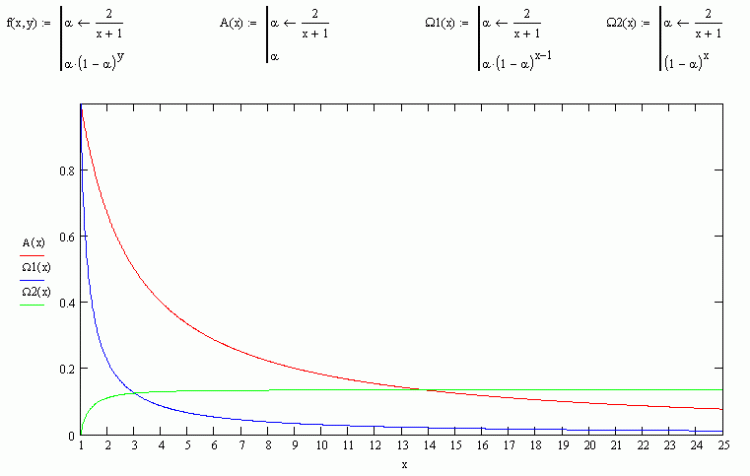
Это с ходу могу. Смотрите. Так как (по моему варианту, согласен) имеем разложение рекурсии в ряд, состоящий из трёх узловых значений: первое, последнее и предпоследнее (или первое, последнее и второе, смотря с какого конца считать), то, если смотреть графики функций их изменения (этих узловых точек от рекурсии к рекурсии), то они пересекаются в точках 3 и 14. Вторая функция - это вес Close[0], третья - Close[Bars-2], четвёртая - Close[Bars-1]. Первая это лишнее, формула рекурсии без остаточного члена.
Тут необходимое пояснение. Как такового периода в смысле окна свечей у ЕМА нет. То, что передаётся как период в ЕМА - это просто договорённость, возможность хоть какого-то управления функцией. Это значение, период больше единицы, инвертируется в значение меньше единицы, которое и используется как множитель эдакой геометрической прогрессии, суммой которой и является ЕМА. То есть например в SMA и WMA период - это окно свечей, т.е. заданное этим периодом их количество, из которых берётся средняя величина, например Close, и отображается как точка непрерывной линии на месте правой границы этого диапазона (окна). В ЕМА количество свечей для подсчёта их среднего значения увеличивается с каждым шагом рекурсии. То есть, говоря простыми словами, с появлением нового бара и продолжением ЕМА вправо возникающая точка машки - это среднее значение всех баров истории. Это я не вам объясняю, это я говорю то, что сам понял, осознал.
По поводу того, зачем так высоко забирать последний вес (это вес Close[Bars-1] кстати). Так пока и не понял, но увидел, что будет, если не забирать. Итак, немного меняем формулу рекурсии:
β=1-α. По левую сторону у нас старый вариант, по правую - чуть-чуть, самую малость изменённый, и что из этого получается. Получается вообщем-то искомый вариант без забора высоты. Меняем код ЕМА. Изменения касаются только формулы начального члена:
//+------------------------------------------------------------------+ //| Exponential Moving Average | //+------------------------------------------------------------------+ void ema() { double pr=2.0/(MA_Period+1); int pos=Bars-2; if(ExtCountedBars>2) pos=Bars-ExtCountedBars-1; //---- main calculation loop while(pos>=0) { if(pos==Bars-2) ExtMapBuffer[pos+1]=pr*Close[pos+1]; ExtMapBuffer[pos]=Close[pos]*pr+ExtMapBuffer[pos+1]*(1-pr); pos--; } }
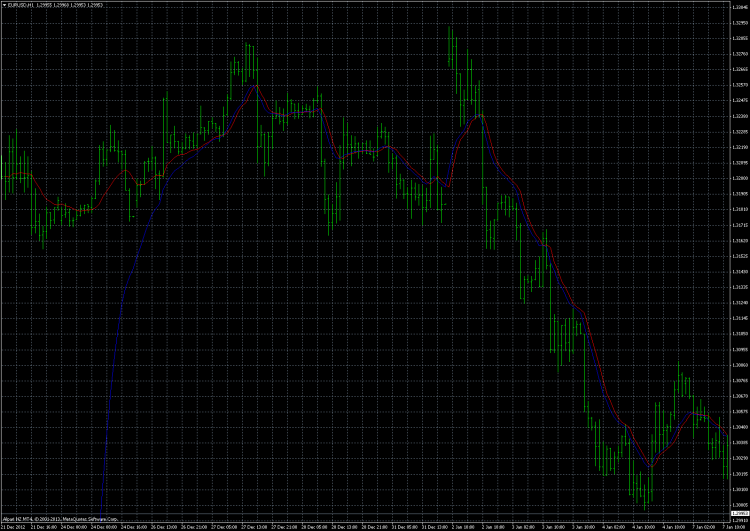
Вешаем обе ЕМА, обычную и модифицированную, ставим shift=1 и разный цвет чтобы не путаться, идём на начало истории, смотрим:
Видал подобную картинку где-то здесь на форуме, но не помню где, может кто-то напомнит.
Сейчас буду разбираться в предложенных материалах.
Это с ходу могу. Смотрите. Так как (по моему варианту, согласен) имеем разложение рекурсии в ряд, состоящий из трёх узловых значений: первое, последнее и предпоследнее (или первое, последнее и второе, смотря с какого конца считать), то, если смотреть графики функций их изменения (этих узловых точек от рекурсии к рекурсии), то они пересекаются в точках 3 и 14. Вторая функция - это вес Close[0], третья - Close[Bars-2], четвёртая - Close[Bars-1]. Первая это лишнее, формула рекурсии без остаточного члена.
Дык неправильно у вас, последний член никуда не задирается, он ведет себя точно так же, как и все остальные (уменьшается), ни с чем не пересекается и в пределе равен 0. Ищите ошибку в расчетах.
Как такового периода в смысле окна свечей у ЕМА нет. То, что передаётся как период в ЕМА - это просто договорённость, возможность хоть какого-то управления функцией.
Называетя "характерный временной параметр". Подбирается так, чтобы средняя временая задержка SMA и EMA с одинаковыми периодами была примерно одинакова.
(2) Откуда вы вывели формулу F(n,x) (" разложение этой рекурсии в ряд " )
P.S. Я с EMA не работал, могу ошибаться, проверяйте
последний член никуда не задирается
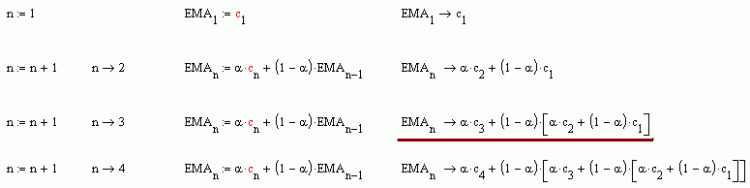
Упростите кто-нибудь подчёркнутое выражение и вынесите альфа за общие скобки, а то у меня ничего не получается.
Явное расхождение между количеством членов цВР и количеством весовых коэффициентов. Похоже напутали с индексами.
Совершенно верно. Я понял, в чём была ошибка - в привычке. У меня привычка начинать счёт с нуля. Соответственно от нуля до двух будет три элемента. Здесь же мы считаем элементы не по порядку их расположения (0, 1, 2...), а по их количеству (1, 2, 3...).
Упростите кто-нибудь подчёркнутое выражение и вынесите альфа за общие скобки, а то у меня ничего не получается.
Не вынесется она, да и не надо.
Кстати, быстрый способ посчитать коэффициенты рекурсивного фильтра - через z-преобразование.
Я, кажется, понял, почему у вас "задирается". Чем "медленнее" машка, тем медленнее должны убывать коэффициенты, следовательно, остаточный член (сумма всего того, что вы выбрасываете) тем больше, чем больше период маши. Проблема в расчетах в том, что вы начинаете с c0 (начальная инициализация), а положено начинать с EMA0. Понятно, что ее еще нет до начала истории баров, поэтому в коде обычно заменяют на SMA. По-моему в стандартной машке МТ так и написано, поправьте, если я неправ.
А чего тут упрощать-то. Выражение в квадратных скобках - это EMA2 (смотри формулу). Соответственно
EMA3 = alpha*c3 + (1-alpha)*EMA2.
Альфу за общие скобки выносить не надо.
А чего тут упрощать-то. Выражение в квадратных скобках - это EMA2 (смотри формулу). Соответственно
EMA3 = alpha*c3 + (1-alpha)*EMA2.
Альфу за общие скобки выносить не надо.
Угу, и приходим опять к формуле рекурсии)))
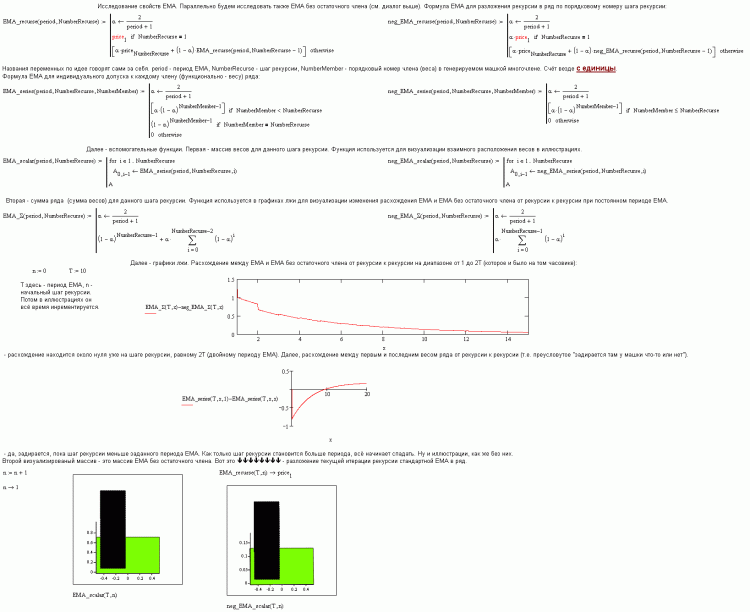
Так, я кажется разобрался. Причина была в неправильном объявлении функций. У ЕМА (только под скальпелем, конечно) три параметра: период, шаг рекурсии и порядковый номер веса в многочлене, генерируемом рекурсией на этом шаге. Период и обратная ему альфа нигде, никоим образом, никем и никак не меняются, это константы. Шаг рекурсии и порядковый номер веса легко спутать, т.к. максимальное значение порядкового номера веса равно этому шагу рекурсии. Соответственно имеем (это только заголовок портянки):
Сама портянка выглядит вот так:

Ничто нигде у машки на Close[0] после прохождения порядка двух тысяч итераций рекурсии после Close[Bars-1] не задирается...
Портянку маткада прикрепляю, там можно и поэкспериментировать с периодом. Маткад, повторюсь, одиннадцатый. Проверяйте, вдруг где-то ошибся.
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования



По просьбе форумчан переношу свою писанину в отдельную ветку, чтобы не захламлять ту ветку, которая была создана для того чтобы не захламлять форум.
Разбирая алгоритм ЕМА с целью в т.ч. возможной оптимизации, решил исследовать генерируемые ею веса. Как известно, там рекурсия. По оригиналу кода:
Взял маткад:
Возник следующий вопрос: зачем надо так высоко задирать последний вес, если можно просто обернуть степенную функцию на по возрастанию, если последующий вес так важнее предыдущего? Попробовал написать скрипт, чтобы протестировать миллисекунды для расчёта ЕМА по рекурсии и по выведенной формуле конечных весов после её окончания (см. F(n,x) в маткадовской портянке)
- разницу что-то не ощутил, всё укладывается в нормальное распределение. Значит, можно рассчитывать как рекурсией, так и по формуле (в т.ч. какой-то другой для этой машки, напр. y(n, x) или инвертированной), на быстродействие они влияют одинаково. Вот выборка из лога:
Лог прикрепляю. Там я убрал все строки со значениями ema1 или ema2, равными 0, 15, 16 (погрешность GetTickCount() по Рошу), а в вышеприведённой выборке из той выборки убраны и все значения с 31, 32.
Кстати говоря, как постскриптум: теперь я понял, почему во многих индикаторах, использующих "экспотенциальную" машку (хотя правильнее её назвать степенной), стоит период равный 14...
Прикрепляю также маткад, всё в архиве. Маткад одиннадцатый. Итак - зачем нужно задирать последний вес? Или я где-то глупо ошибся?...