Discussão do artigo "Redes Neurais de Terceira Geração: Redes Profundas" - página 2

Novo comentário
 
vlad1949:

Não é uma pergunta para mim. Isso é tudo o que você tem a dizer sobre o artigo?

O que há sobre o artigo? É uma reescrita típica. É a mesma coisa em outras fontes, apenas com palavras ligeiramente diferentes. Até as fotos são as mesmas. Não vi nada de novo, ou seja, de autoral.

Eu queria experimentar os exemplos, mas é uma chatice. A seção é para MQL5, mas os exemplos são para MQL4.

 

vlad1949

Caro Vlad!

Ao dar uma olhada nos arquivos, você tem uma documentação do R bastante antiga. Seria bom mudar para as cópias anexadas.

Arquivos anexados:
Doc_R.zip  2181 kb
 

vlad1949

Caro Vlad!

Por que você não conseguiu executar no testador?

Eu tenho tudo funcionando sem problemas. Mas o esquema não tem um indicador: o Expert Advisor se comunica diretamente com o R.

 

Jeffrey Hinton, inventor das redes profundas: "As redes profundas só são aplicáveis a dados em que a relação sinal-ruído é grande. As séries financeiras são tão ruidosas que as redes profundas não são aplicáveis. Nós tentamos e não tivemos sorte".

Ouça suas palestras no YouTube.

 
gpwr:

Jeffrey Hinton, inventor das redes profundas: "As redes profundas só são aplicáveis a dados em que a relação sinal-ruído é grande. As séries financeiras são tão ruidosas que as redes profundas não são aplicáveis. Nós tentamos e não tivemos sorte".

Ouça as palestras dele no YouTube.

Considerando sua postagem no tópico paralelo.

O ruído é entendido de forma diferente nas tarefas de classificação e na engenharia de rádio. Um preditor é considerado ruidoso se estiver fracamente relacionado (tiver um poder de previsão fraco) à variável de destino. Um significado completamente diferente. Deve-se procurar preditores que tenham poder de previsão para diferentes classes da variável de destino.

 
Tenho um entendimento semelhante de ruído. As séries financeiras dependem de um grande número de preditores, a maioria dos quais é desconhecida para nós e que introduzem esse "ruído" na série. Usando apenas preditores disponíveis publicamente, não conseguimos prever a variável-alvo, independentemente das redes ou dos métodos que usamos.
 
gpwr:
Tenho um entendimento semelhante de ruído. As séries financeiras dependem de um grande número de preditores, a maioria dos quais é desconhecida para nós e que introduzem esse "ruído" na série. Usando apenas os preditores disponíveis publicamente, não conseguimos prever a variável-alvo, independentemente das redes ou dos métodos que usamos.
Veja meu tópico.
 
faa1947:

vlad1949

Caro Vlad!

Por que você não conseguiu executar no testador?

Eu tenho tudo funcionando sem problemas. É verdade o esquema sem um indicador: o consultor se comunica diretamente com o R.

llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll

Boa tarde, SanSanych.

Portanto, a ideia principal é criar uma multimoeda com vários indicadores.

Caso contrário, é claro, você pode colocar tudo em um Expert Advisor.

Mas se o treinamento, o teste e a otimização forem implementados em tempo real, sem interromper a negociação, a variante com um Consultor especialista será um pouco mais difícil de implementar.

Boa sorte

PS. Qual é o resultado dos testes?

 

Saudações, SanSanych.

Aqui estão alguns exemplos de determinação do número ideal de clusters que encontrei em um fórum de língua inglesa. Não consegui usar todos eles com meus dados. Muito interessante o pacote 11 "clusterSim".

--------------------------------------------------------------------------------------

#
n = 100
g = 6 
set.seed(g)
d <- data.frame(x = unlist(lapply(1:g, function(i) rnorm(n/g, runif(1)*i^2))), 
                y = unlist(lapply(1:g, function(i) rnorm(n/g, runif(1)*i^2))))
plot(d)
--------------------------------------
#1 
library(fpc)
pamk.best <- pamk(d)
cat("number of clusters estimated by optimum average silhouette width:", strpamk.best$nc, "\n")
plot(pam(d, pamk.best$nc))

#2 we could also do:
library(fpc)
asw <- numeric(20)
for (k in 2:20)
  asw[[k]] <- pam(d, k) $ silinfo $ avg.width
k.best <- which.max(asw)
cat("silhouette-optimal number of clusters:", k.best, "\n")
---------------------------------------------------
#3. Calinsky criterion: Another approach to diagnosing how many clusters suit the data. In this case 
# we try 1 to 10 groups.
require(vegan)
fit <- cascadeKM(scale(d, center = TRUE,  scale = TRUE), 1, 10, iter = 1000)
plot(fit, sortg = TRUE, grpmts.plot = TRUE)
calinski.best <- as.numeric(which.max(fit$results[2,]))
cat("Calinski criterion optimal number of clusters:", calinski.best, "\n")
# 5 clusters!
-------------------
4. Determine the optimal model and number of clusters according to the Bayesian Information 
Criterion for expectation-maximization, initialized by hierarchical clustering for parameterized 
Gaussian mixture models
library(mclust)
# Run the function to see how many clusters
# it finds to be optimal, set it to search for
# at least 1 model and up 20.
d_clust <- Mclust(as.matrix(d), G=1:20)
m.best <- dim(d_clust$z)[2]
cat("model-based optimal number of clusters:", m.best, "\n")
# 4 clusters
plot(d_clust)
----------------------------------------------------------------
5. Affinity propagation (AP) clustering, see http://dx.doi.org/10.1126/science.1136800 
library(apcluster)
d.apclus <- apcluster(negDistMat(r=2), d)
cat("affinity propogation optimal number of clusters:", length(d.apclus@clusters), "\n")
# 4
heatmap(d.apclus)
plot(d.apclus, d)
---------------------------------------------------------------------
6. Gap Statistic for Estimating the Number of Clusters. 
See also some code for a nice graphical 
output . Trying 2-10 clusters here:
library(cluster)
clusGap(d, kmeans, 10, B = 100, verbose = interactive())
-----------------------------------------------------------------------
7. You may also find it useful to explore your data with clustergrams to visualize cluster 
assignment, see http://www.r-statistics.com/2010/06/clustergram-visualization-and-diagnostics-for-cluster-analysis-r-code/&nbsp; 
for more details.
-------------------------------------------------------------------
#8. The NbClust package  provides 30 indices to determine the number of clusters in a dataset.
library(NbClust)
nb <- NbClust(d, diss = NULL, distance = "euclidean", 
        min.nc=2, max.nc=15, method = "kmeans", 
        index = "alllong", alphaBeale = 0.1)
hist(nb$Best.nc[1,], breaks = max(na.omit(nb$Best.nc[1,])))
# Looks like 3 is the most frequently determined number of clusters
# and curiously, four clusters is not in the output at all!
-----------------------------------------
Here are a few examples:
d_dist <- dist(as.matrix(d))   # find distance matrix 
plot(hclust(d_dist))           # apply hirarchical clustering and plot
----------------------------------------------------
#9 Bayesian clustering method, good for high-dimension data, more details:
# http://vahid.probstat.ca/paper/2012-bclust.pdf
install.packages("bclust")
library(bclust)
x <- as.matrix(d)
d.bclus <- bclust(x, transformed.par = c(0, -50, log(16), 0, 0, 0))
viplot(imp(d.bclus)$var); 
plot(d.bclus); 
ditplot(d.bclus)
dptplot(d.bclus, scale = 20, horizbar.plot = TRUE,varimp = imp(d.bclus)$var, horizbar.distance = 0, dendrogram.lwd = 2)
-------------------------------------------------------------------------
#10 Also for high-dimension data is the pvclust library which calculates 
#p-values for hierarchical clustering via multiscale bootstrap resampling. Here's #the example from the documentation (wont work on such low dimensional data as in #my example):
library(pvclust)
library(MASS)
data(Boston)
boston.pv <- pvclust(Boston)
plot(boston.pv)
------------------------------------
###Automatically cut the dendrogram
require(dynamicTreeCut)
ct_issues <- cutreeHybrid(hc_issues, inverse_cc_combined, minClusterSize=5)
-----
FANNY <- fanny(as.dist(inverse_cc_combined),, k = 3, maxit = 2000) 
FANNY$membership MDS <- smacofSym(distMat)$conf 
plot(MDS, type = "n") text(MDS, label = rownames(MDS), col = rgb((FANNY$membership)^(1/1)))
-----
m7 <- stepFlexmix
----------------------
#11 "clusterSim" -Department of Econometrics and Computer Science, University of #Economics, Wroclaw, Poland
http://keii.ue.wroc.pl/clusterSim
See file ../doc/clusterSim_details.pdf for further details
data.Normalization Types of variable (column) and object (row) normalization formulas
Description
Types of variable (column) and object (row) normalization formulas
Usage
data.Normalization (x,type="n0",normalization="column")
Arguments
x vector, matrix or dataset
type type of normalization: n0 - without normalization
n1 - standardization ((x-mean)/sd)
n2 - positional standardization ((x-median)/mad)
n3 - unitization ((x-mean)/range)
n3a - positional unitization ((x-median)/range)
n4 - unitization with zero minimum ((x-min)/range)
n5 - normalization in range <-1,1> ((x-mean)/max(abs(x-mean)))
n5a - positional normalization in range <-1,1> ((x-median)/max(abs(x-median)))
n6 - quotient transformation (x/sd)
n6a - positional quotient transformation (x/mad)
n7 - quotient transformation (x/range)
n8 - quotient transformation (x/max)
n9 - quotient transformation (x/mean)
n9a - positional quotient transformation (x/median)
n10 - quotient transformation (x/sum)
n11 - quotient transformation (x/sqrt(SSQ))
normalization "column" - normalization by variable, "row" - normalization by objec
See file ../doc/HINoVMod_details.pdf for further details


Na próxima postagem, cálculos com meus dados

 

O número ideal de clusters pode ser determinado por vários pacotes e usando mais de 30 critérios de otimização. De acordo com minhas observações, o critério mais usado é ocritério de Calinsky.

Vamos pegar os dados brutos de nosso conjunto do indicador dt . Ele contém 17 preditores, alvo y e corpo de candlestick z.

Nas versões mais recentes dos pacotes "magrittr" e "dplyr", há muitos novos recursos interessantes, um deles é o 'pipe' - %>%. Ele é muito conveniente quando não é necessário salvar resultados intermediários. Vamos preparar os dados iniciais para o agrupamento. Pegue a matriz inicial dt, selecione as últimas 1.000 linhas dela e, em seguida, selecione 17 colunas de nossas variáveis. Obtemos uma notação mais clara, nada mais.

> library(magrittr)
> x<-dt %>% tail( .,1000)%>% extract( ,1:17)

1.

> library(fpc)
> pamk.best <- pamk(x)
> cat("number of clusters estimated by optimum average silhouette width:", pamk.best$nc, "\n")
> number of clusters estimated by optimum average silhouette width: h: 2

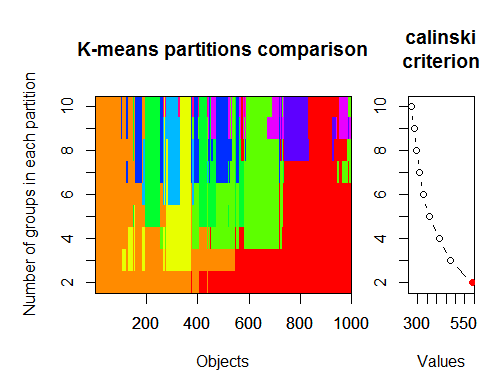
2. Critério de Calinsky: outra abordagem para diagnosticar quantos clusters são adequados aos dados. Nesse caso

tentamos de 1 a 10 grupos.

> require(vegan)
> fit <- cascadeKM(scale(x, center = TRUE,  scale = TRUE), 1, 10, iter = 1000)
> plot(fit, sortg = TRUE, grpmts.plot = TRUE)

> calinski.best <- as.numeric(which.max(fit$results[2,]))
> cat("Calinski criterion optimal number of clusters:", calinski.best, "\n")
Calinski criterion optimal number of clusters: 2
3) Determine o modelo ideal e o número de clusters de acordo com o Critério de Informação Bayesiano para maximização de expectativa, inicializado por clusterização hierárquica para modelos de mistura gaussiana parametrizados.

Modelos de mistura gaussiana 

> library(mclust)
#  Run the function to see how many clusters
#  it finds to be optimal, set it to search for
#  at least 1 model and up 20.
> d_clust <- Mclust(as.matrix(x), G=1:20)
> m.best <- dim(d_clust$z)[2]
> cat("model-based optimal number of clusters:", m.best, "\n")
model-based optimal number of clusters: 7
123456789...17
Novo comentário