Obrigado pelo artigo interessante.
É uma pena que haja poucas explicações sobre os códigos.
E algo está errado com o código python, instalei todas as bibliotecas, mas no terminal recebo o seguinte:
learning time = 1228.5106182098389
solver = lbfgs
loss = 0.0024399556870102
iter = 300
C:\Users\User\AppData\Local\Programs\Python\Python39\lib\site-packages\sklearn\neural_network\_multilayer_perceptron.py:545: ConvergenceWarning: lbfgs failed to converge (status=1): in '' (0,0)
STOP: TOTAL NO. of ITERATIONS REACHED LIMIT. in '' (0,0)
Increase the number of iterations (max_iter) or scale the data as shown in: in '' (0,0)
https://scikit-learn.org/stable/modules/preprocessing.html in '' (0,0)
self.n_iter_ = _check_optimize_result("lbfgs", opt_res, self.max_iter) in '' (0,0)
Traceback (most recent call last): in '' (0,0)
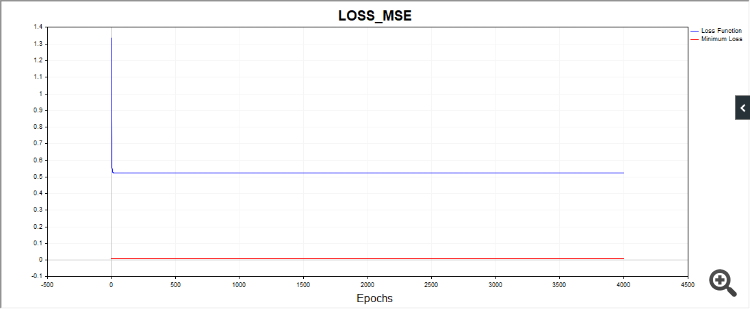
plt.plot(np.log(pd.DataFrame(clf.loss_curve_))) in 'SklearnMLP.py' (59,0)
AttributeError: 'MLPRegressor' object has no attribute 'loss_curve_' in 'SklearnMLP.py' (59,0)
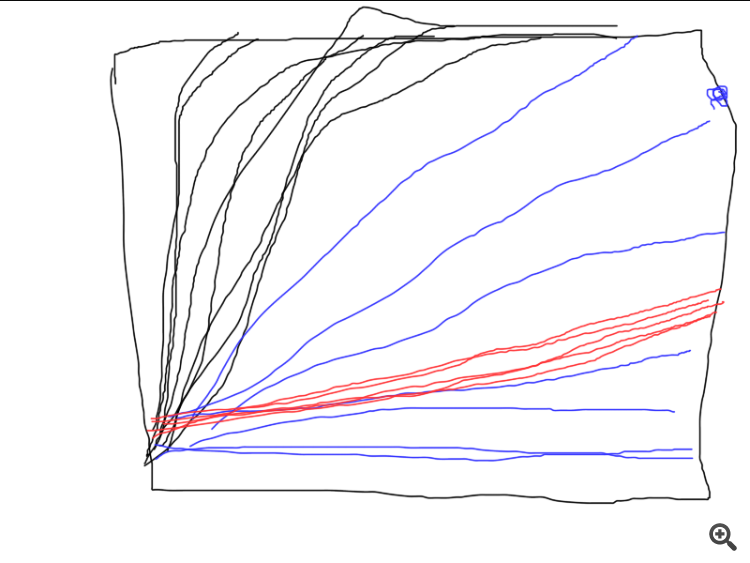
Mais uma coisa, o script SD em alguns casos desenha essa imagem:
Ou seja, o algoritmo está preso, aparentemente, em uma data simples.
Outros códigos também produzem resultados de convergência muito diferentes. Portanto, é desejável fornecer gráficos de uma série de testes independentes; as imagens de testes únicos nos dizem pouco (praticamente nada).
Obrigado pelo feedback.
Em python. Não é um erro, ele avisa que o algoritmo foi interrompido porque atingimos o limite de iteração. Ou seja, o algoritmo parou antes que o valor tol = 0,000001 fosse atingido. E então ele avisa que o otimizador lbfgs não tem um atributo "loss_curve", ou seja, dados da função de perda. Para o adam e o sgd, eles têm, mas para o lbfgs, por algum motivo, não têm. Provavelmente eu deveria ter criado um script para que, quando o lbfgs fosse iniciado, ele não solicitasse essa propriedade para não confundir as pessoas.
No SD. Como começamos cada vez a partir de pontos diferentes no espaço de parâmetros, os caminhos para a solução também serão diferentes. Fiz muitos testes e, às vezes, realmente são necessárias mais iterações para convergir. Tentei fornecer um número médio de iterações. Você pode aumentar o número de iterações e verá que o algoritmo converge no final.
Em SD. Como começamos cada vez a partir de um ponto diferente no espaço de parâmetros, os caminhos para convergir para uma solução também serão diferentes. Fiz muitos testes e, às vezes, realmente são necessárias mais iterações para convergir. Tentei fornecer um número médio de iterações. Você pode aumentar o número de iterações e verá que o algoritmo converge no final.
É disso que estou falando. É a robustez, ou seja, a reprodutibilidade dos resultados. Quanto maior a dispersão dos resultados, mais próximo o algoritmo está do RND para um determinado problema.
Aqui está um exemplo de como três algoritmos diferentes funcionam. Qual deles é o melhor? A menos que você execute uma série de testes independentes e calcule os resultados médios (idealmente, calcule e compare a variação dos resultados finais), é impossível comparar.
É sobre isso que estou falando. É a estabilidade, ou seja, a reprodutibilidade dos resultados. Quanto maior a dispersão dos resultados, mais próximo o algoritmo está do RND para um determinado problema.
Aqui está um exemplo de como três algoritmos diferentes funcionam. Qual deles é o melhor? A menos que você execute uma série de testes independentes e calcule os resultados médios (idealmente, calcule e compare a variação dos resultados finais), é impossível comparar.
Em seguida, é necessário definir o critério de avaliação.
Não, nesse caso você não precisa se dar a esse trabalho, mas se estiver comparando métodos diferentes, poderá adicionar outro ciclo (testes independentes) e exibir os gráficos de testes individuais. Tudo ficaria muito claro, quem converge, quão estável é e quantas iterações são necessárias. E assim acabou sendo "como da última vez", quando o resultado é ótimo, mas apenas uma vez em um milhão.
De qualquer forma, obrigado, o artigo me deu algumas ideias interessantes.
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Novo artigo Treinamento de perceptron multicamadas com o algoritmo de Levenberg-Marquardt foi publicado:
O objetivo deste artigo é oferecer aos traders praticantes um algoritmo muito eficiente para o treinamento de redes neurais, que é uma variante do método de otimização de Newton conhecida como algoritmo de Levenberg-Marquardt. Este é um dos algoritmos mais rápidos para treinar redes neurais com propagação para frente, rivalizando apenas com o algoritmo de Broyden-Fletcher-Goldfarb-Shanno (L-BFGS).
Métodos estocásticos de otimização, como a descida do gradiente estocástica (SGD) e Adam, são bastante adequados para treinamento offline, quando o retreinamento da rede neural ocorre em intervalos longos. No entanto, se o trader que utiliza redes neurais deseja que o modelo se adapte rapidamente às condições de mercado em constante mudança, é necessário treiná-lo novamente a cada nova barra, ou em intervalos curtos. Nesses casos, são mais indicados algoritmos que utilizam não só a informação do gradiente da função de perda, mas também informações adicionais das segundas derivadas parciais, o que permite encontrar um mínimo local da função de perda em poucas épocas de treinamento.
Até onde sei, não há nenhuma implementação do algoritmo de Levenberg-Marquardt em MQL5 disponível publicamente. Está na hora de preencher essa lacuna e, ao mesmo tempo, revisar brevemente os algoritmos de otimização mais conhecidos e simples, como a descida do gradiente, a descida do gradiente com impulso (momentum) e a descida do gradiente estocástica. Ao final do artigo, faremos um pequeno teste de eficácia do algoritmo de Levenberg-Marquardt em comparação com os algoritmos da biblioteca scikit-learn para aprendizado de máquina.
Autor: Evgeniy Chernish