방정식의 평등을 만든 다음 미분해야 할 것 같습니다 (짧은 경로를 따라 저속으로 경작지를 따라 경로를 자르거나 아스팔트를 따라 운전할 수있을 때 문제는 구급차를 생각 나게합니다. 더 빠른 속도이지만 더 긴 경로를 따라 - 아스팔트에서 경작지로 이동할 곳은 어디입니까?).
그래서 문제는 그것들을 만드는 방법입니다. 지금까지는 반복 형식으로만 얻을 수 있습니다.
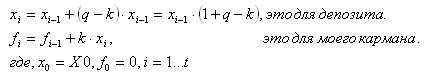
이것을 분석적 형태(시간 t 에 대한 기능적 의존성의 형태로)로 제시할 필요가 있습니다.
f에 대한 공식을 더 확장하십시오. fi = fi(x0)로 가져옵니다.
아하! 그러면 다음과 같이 나타납니다.
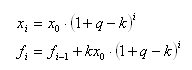
그리고 t개월 동안 인출된 금액에 대한 표현은 다음과 같이 쓸 수 있습니다.
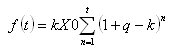
그렇다면 더 좋습니다. 무엇 향후 계획? 버려야지...
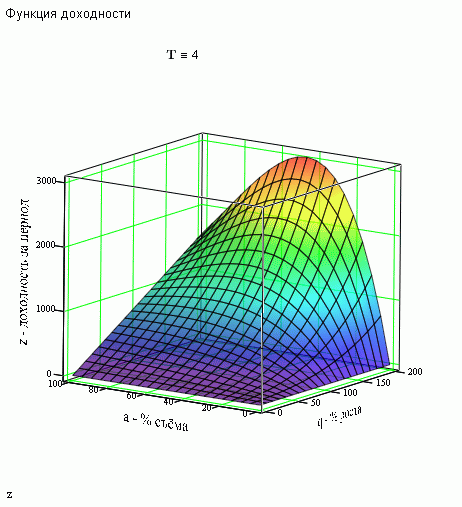
다음과 같이 보일 것입니다.
네피세!...
그리고 더 자세하게 가능합니까? 공식의 형태로 말이에요.
저것들. 실제로 최적의 제거 비율이 보입니다!
여기서 q는 GP 분모이고 b1은 첫 번째 항입니다.
alsu :
기하학적 진행의 처음 n개 항의 합에 대한 공식을 기억하십시오.
사탄! 정말로, 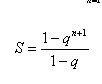 .
.
그런 다음 마지막으로 인출 된 자금 금액에 대한 표현식은 다음과 같이 표시됩니다.
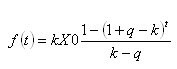
시간에 대한 도함수를 취하여 0과 동일시하는 것이 남아 있습니다... Mda-ah-ah.
Neutron :
그리고 q를 쏠 필요가 있고 기간 t가 끝날 때만 쏠 필요가 있다는 것은 당연합니다. 다른 모든 경우에는 인출 금액이 적습니다.
안녕하세요 여러분!
나는 X0 루블의 보증금을 사용할 수있었습니다. t 개월 이내. 매월 예금 X 의 현재 가치에서 일정 비율의 자금 q 가 예금으로 청구됩니다. 매월 q 를 초과하지 않는 일부 비율 k 를 계정에서 인출할 수 있습니다.
따라서 과제는 t 개월 동안 인출된 금액을 최대화하는 것입니다.
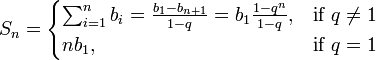
안녕하세요 여러분!
나는 X0 루블의 보증금을 사용할 수있었습니다. t 개월 이내. 매월 예금 X 의 현재 가치에서 일정 비율의 자금 q 가 예금으로 청구됩니다. 매월 q 를 초과하지 않는 일부 비율 k 를 계정에서 인출할 수 있습니다.
따라서 과제는 t 개월 동안 인출된 금액을 최대화하는 것입니다. 매월 전체 미지급이자 q 를 인출하는 것이 최선의 선택이 아닌 것은 분명한 것 같습니다. 이 경우 예금은 증가하지 않으며 계정의 부하가 낮을수록 결과적으로 인출 된 금액이 더 커질 수 있습니다 ... 반면 k 값은 0이되는 경향이 없어야합니다. 왜냐하면 이 경우 인출 금액도 0이 되는 경향이 있습니다. 분명히 진실은 그 중간 어딘가에 있습니다. 하지만 정확히 어디에?
이 문제를 분석적으로 해결하도록 도와주세요.
추신: 스레드 거래와 관련이 없는 문제 는 게시하지 않았습니다. 제안된 주제는 후자와 관련이 있습니다.