따라서 직각 삼각형의 면적은 항상 빗변으로 다음과 같이 표현할 수 있습니다. S = c^2 * f(alpha) , 여기서 f 는 일부 함수입니다.
그림에서 각 1과 2는 같습니다( alpha ).
큰 삼각형의 면적은 작은 삼각형 면적의 합과 같습니다: S = S1 + S2 또는 항목 2. 그래서 c^2 * f(alpha) = a^2 * f(alpha) + b^2 * f(alpha) 입니다.
여기서 우리는 c^2 = a^2 + b^2 를 얻습니다.
주요 단순(비표준) 아이디어는 항목 2입니다. 유사한 삼각형의 속성에 대한 지식은 사용되지 않으며, 함수 f 의 존재를 이해하기 위해 삼각법에 대한 지식도 필요하지 않습니다. 저것들. 그러한 증명은 초등학교에서 아이들이 어떤 영역인지 잘 설명한 후(평소와 달리) 주어질 수 있습니다.
최근에 방문했고 두 개의 석조 피라미드(이집트 피라미드와 같은)를 보았습니다. 나는 그것들을 손에 들고 받침대와 함께 붙였습니다(크기가 약간 다름).
그리고 그는 피타고라스 정리의 또 다른 증거를 제시했습니다(구성에서 분명함).
Integer : Весь процесс уперся в производную? Вот эта функция - x0*k*(1-(1+q-k)^2)/(k-q)? Если это так, то это как бы не проблема, я их легко решал, только вспомнить надо немного. Переменная q?
몰라, 이게 무슨 수식인지 써놓고 변수를 다 정의해놨어. 나는 또한 분명히 할 것입니다 - 이것은 매월 인출되는 이익 금액입니다 (m 개월 동안의 총 이익이 아님).
시리즈의 합계에 대한 공식을 도출하는 것이 남아 있습니다. 당신은 쉽게 할 수 있다고 썼습니다. 그런 다음 0과 같은 미분을 취하십시오 ...
내 표기법에 따르면 이번 달에 인출된 자금 공식은 다음과 같습니다.
따라서 이 함수의 동물 유사 파생물은 위의 함수만큼 깎기 어렵습니다.
f 를 미리 계산한 다음 최대값을 찾을 수 있다고 생각합니다. 아마도 이 방법이 더 쉬울 것입니다.
자동 :
그런 다음 두 번째 단계에서 흐름을 두 부분으로 나누는 밸브를 엽니다. 이것은 입력 스트림을 변경합니다.
해결책이 보일 때까지?
아니요, 정확히 어떻게 계획했는지 알 수 없습니다. 말해 주세요.
그들의 해석에서 피타고라스 정리를 이해하지 못하는 사람들이 있습니다.
오프탑:
학교에서 그들은 피타고라스 정리의 가장 간결한 증거를 제시했습니다.
주요 단순(비표준) 아이디어는 항목 2입니다. 유사한 삼각형의 속성에 대한 지식은 사용되지 않으며, 함수 f 의 존재를 이해하기 위해 삼각법에 대한 지식도 필요하지 않습니다. 저것들. 그러한 증명은 초등학교에서 아이들이 어떤 영역인지 잘 설명한 후(평소와 달리) 주어질 수 있습니다.
오프탑:
학교에서 그들은 피타고라스 정리의 가장 간결한 증거를 제시했습니다.
어떤 수업에서?
공식 S = c^2 * f(alpha) 는 7학년 학생에게 명확하지 않습니다. 이것은 유형이 그렇습니다.
따라서 이 함수의 동물 유사 파생물은 위의 함수만큼 깎기 어렵습니다.
전체 프로세스가 파생 상품으로 실행되었습니까?
이 함수는 x0*k*(1-(1+qk)^2)/(kq)?
그렇다면 이것은 문제가 아니며 쉽게 해결했습니다. 조금만 기억하면됩니다. 변수 q?
어떤 수업에서?
공식 S = c^2 * f(alpha) 는 7학년 학생에게 명확하지 않습니다. 이것은 유형이 그렇습니다.
위의 증명을 이해하는 데 특별한 어려움이 없다고 느낄 정도로 도형의 영역 개념을 잘 소개받은 거의 모든 어린이.
어린이가 면적이 무엇인지 진정으로 이해하면 치수 측정을 이해하고 그림을 고유하게 결정하는 특성 (이 경우 빗변 및 각도)을 통해 모든 그림의 면적을 표현할 수 있음을 이해합니다. .
유사한 삼각형 및 삼각법의 속성에 대한 지식은 필요하지 않습니다.
최근에 방문했고 두 개의 석조 피라미드(이집트 피라미드와 같은)를 보았습니다. 나는 그것들을 손에 들고 받침대와 함께 붙였습니다(크기가 약간 다름).
그리고 그는 피타고라스 정리의 또 다른 증거를 제시했습니다(구성에서 분명함).
Integer :
Весь процесс уперся в производную?
Вот эта функция - x0*k*(1-(1+q-k)^2)/(k-q)?
Если это так, то это как бы не проблема, я их легко решал, только вспомнить надо немного. Переменная q?
아니요, 문제는 k 에 대한 도함수입니다.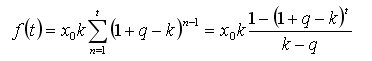
그것은 0과 동일해야 하고 k 에 대해 풀어야 합니다.
똑똑히 할 수 없어 간단하게 그려볼게
기간이 시작될 때 저장소가 10,000이라고 가정해 보겠습니다. 각 기간마다 5%가 디포에 적립되며 디포에 재투자됩니다. 각 기간에 3%만 인출할 수 있습니다.
각 기간에 3%를 모두 인출하면 총 $4,000 이상을 가져갈 것입니다(저장소에서 낭비). ).
위의 증명을 이해하는 데 특별한 어려움이 없다고 느낄 정도로 도형의 영역 개념을 잘 소개받은 거의 모든 어린이.
어린이가 면적이 무엇인지 진정으로 이해하면 치수 측정을 이해하고 그림을 고유하게 결정하는 특성 (이 경우 빗변 및 각도)을 통해 모든 그림의 면적을 표현할 수 있음을 이해합니다. .
그러나 이것은 엄격한 증거가 아닙니다.
똑똑히 할 수 없어 간단하게 그려볼게
이러한 표를 그리는 것이 아니라 두 개의 입력 값을 간단한 수식으로 대체하고 답을 얻기 위해서는 일반적인 분석 솔루션이 필요한 이유입니다.
문제의 사실은 위의 모든 것이 "그렇게 될 것 같다"는 것입니다. "이건 어떻게든 뭔가를 통해 표현될 수 있어."
그러나 이것은 엄밀한 증거가 아닙니다.
엄밀한 증거가 아닌 것은?! 그것은 분명합니다: