논리적으로. 해결책은 다음과 같습니다. 흥미롭게도, 무게를 두 컵에 동시에 놓을 수 있다면 작업이 훨씬 더 어렵고 흥미로워집니다. 그것은 그녀를 고문할 것입니다. 그러나 나에게 알려진 해결책은 없습니다. 어쨌든 최소 가중치의 가중치는 1인 것으로 밝혀졌습니다. 그러나 이것이 자동으로 2의 거듭제곱으로 간다는 의미는 아닙니다.
Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет. Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
Mathemat>> : Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет. Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
컴퓨터가 수학을 했어요 :) 두 컵에 동시에 추를 놓을 수 있는 경우 문제는 2136개의 솔루션이 있습니다(정확히 63개의 추를 균형을 맞출 수 있음). 실제로 모든 솔루션에는 가중치가 1인 가중치가 포함됩니다.
최소값이 1이라는 증명은 쉽습니다. 가능한 최대 가중치는 6개 숫자의 합과 같고 가장 가까운 숫자는 5(최소 가중치 없이 6개)의 합과 같습니다. 최대 가중치와 가장 가까운 가중치의 차이는 1과 같아야 합니다. 따라서 최소값은 1과 같습니다. ihor , 입증되었길 바랍니다. 네, 눈물을 흘리며 프로그램을 요청합니다.
Mathemat>> : Доказательство того, что минимальная - 1, несложно: максимально возможный вес равен сумме всех шести чисел, а тот, что ближайший к нему, равен сумме пяти (шесть без минимальной гирьки). Разница между максимальным и ближайшим к нему весом должна быть равна 1. Следовательно, минимальная равна 1. ihor , доказано, надеюсь? Ага, слезно просим программку.
증명은 특별히 엄격하지는 않지만 정확합니다. 그림과 같이 꼭짓점 좌표에 대한 표기법을 소개하겠습니다. 파란색이 정사각형이 되려면
x1-x2=y1-y4 ; y1-y2=x1-x2;
만큼 잘
x3-x4=y2-y3; y4-y3=x2-x3.
처음 두 방정식에서 그래프의 방정식을 기억하면 다음을 얻습니다.
x4-x2=A(sinx2-sinx4),
세 번째와 네 번째부터
x3-x1=A(sinx1-sinx3).
최소 개수를 제외하고는 사각형에 제한이 없으므로 사각형이 원점을 기준으로 대칭인 경우만 고려합니다. 그러나 x4=-x2, x3=-x1 및 사인과 동일합니다. 방정식은 다음과 같은 형식을 취합니다.
죄(2*x2)/(2*x2)=1/A 죄(2*x1)/(2*x1)=1/A
x2와 x1의 함수가 좌변에 어떤 종류의 그래프를 가지고 있는지 기억합시다. 이렇게 하려면 그림을 살펴보겠습니다. 차트에는 양수 x와 음수 x 모두에 대해 감소하는 극값이 있습니다. 분명히 숫자 A를 점진적으로 줄이면 1978년 등을 포함하여 필요한 만큼의 근을 얻을 수 있습니다. 얻은 뿌리는 다르며 순전히 비합리적으로 서로 관련되어 있습니다. 이 경우의 제곱이 쌍으로 같지 않다는 것을 자세히 증명할 필요는 없다고 생각합니다.
PS Вероятно, предполагается, что гири можно ставить только на одну чашку весов. На другой - груз.
Одно решение очевидно: 1, 2, 4, 8, 16, 32.
1,2,4,8,16,32만이 답이다
어떤 가중치의 가중치가 2^n보다 작으면 총 가중치는 63보다 작습니다.
더 많은 경우 이러한 가중치로 얻을 수 있는 가중치 시퀀스에 간격이 있습니다.
흥미롭게도, 무게를 두 컵에 동시에 놓을 수 있다면 작업이 훨씬 더 어렵고 흥미로워집니다. 그것은 그녀를 고문할 것입니다. 그러나 나에게 알려진 해결책은 없습니다.
어쨌든 최소 가중치의 가중치는 1인 것으로 밝혀졌습니다. 그러나 이것이 자동으로 2의 거듭제곱으로 간다는 의미는 아닙니다.
다음(10일):
Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет.
Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
최소 무게 1 - 확실하지 않음
아마도 두 개의 가중치 2와 3도 작동할 것입니다.
Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет.
Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
컴퓨터가 수학을 했어요 :)
두 컵에 동시에 추를 놓을 수 있는 경우 문제는 2136개의 솔루션이 있습니다(정확히 63개의 추를 균형을 맞출 수 있음).
실제로 모든 솔루션에는 가중치가 1인 가중치가 포함됩니다.
컴퓨터가 수학을 했어요 :)
두 컵에 동시에 추를 놓을 수 있는 경우 문제는 2136개의 솔루션이 있습니다(정확히 63개의 추를 균형을 맞출 수 있음).
실제로 모든 솔루션에는 가중치가 1인 가중치가 포함됩니다.
프로그램을 게시하시겠습니까? 제발 제발!
네, 눈물을 흘리며 프로그램을 요청합니다.
Доказательство того, что минимальная - 1, несложно: максимально возможный вес равен сумме всех шести чисел, а тот, что ближайший к нему, равен сумме пяти (шесть без минимальной гирьки). Разница между максимальным и ближайшим к нему весом должна быть равна 1. Следовательно, минимальная равна 1. ihor , доказано, надеюсь?
Ага, слезно просим программку.
1에 대해 나는 틀렸다.
프로그램에 흥미로운 것은 없으며 단순한 열거입니다.
#include <stdio.h>
#정의 COUNT 63
부울 isOK(int v0,int v1,int v2,int v3,int v4,int v5){
부울 arr[COUNT];
for(int i=0;i<COUNT;i++) arr[i]=거짓;
// 1 - 한 그릇에, 0 - 케틀벨이 포함되지 않음 -1 - 두 번째 그릇에
for(int i0=-1;i0<=1;i0++)
for(int i1=-1;i1<=1;i1++)
for(int i2=-1;i2<=1;i2++)
for(int i3=-1;i3<=1;i3++)
for(int i4=-1;i4<=1;i4++)
for(int i5=-1;i5<=1;i5++) {
정수 = v0*i0+v1*i1+v2*i2+v3*i3+v4*i4+v5*i5;
if (ves > COUNT) false를 반환합니다.
if(ves>0) arr[ves-1]=참;
}
for(int i=0;i<COUNT;i++)
if(!arr[i]) false를 반환합니다.
true를 반환합니다.
}
기본(){
for(int i0=1;i0<COUNT;i0++)
for(int i1=i0;i1<=COUNT-i0;i1++)
for(int i2=i1;i2<=COUNT-i0-i1;i2++)
for(int i3=i2;i3<=COUNT-i0-i1-i2;i3++)
for(int i4=i3;i4<=COUNT-i0-i1-i2-i3;i4++)
for(int i5=i4;i5<=COUNT-i0-i1-i2-i3-i4;i5++)
if (isOK(i0,i1,i2,i3,i4,i5))
printf("%d %d %d %d %d %d\n",i0,i1,i2,i3,i4,i5);
}
Следующая (10-й):
증명은 특별히 엄격하지는 않지만 정확합니다.
그림과 같이 꼭짓점 좌표에 대한 표기법을 소개하겠습니다. 파란색이 정사각형이 되려면
x1-x2=y1-y4 ;
y1-y2=x1-x2;
만큼 잘
x3-x4=y2-y3;
y4-y3=x2-x3.
처음 두 방정식에서 그래프의 방정식을 기억하면 다음을 얻습니다.
x4-x2=A(sinx2-sinx4),
세 번째와 네 번째부터
x3-x1=A(sinx1-sinx3).
최소 개수를 제외하고는 사각형에 제한이 없으므로 사각형이 원점을 기준으로 대칭인 경우만 고려합니다. 그러나 x4=-x2, x3=-x1 및 사인과 동일합니다. 방정식은 다음과 같은 형식을 취합니다.
죄(2*x2)/(2*x2)=1/A
죄(2*x1)/(2*x1)=1/A
x2와 x1의 함수가 좌변에 어떤 종류의 그래프를 가지고 있는지 기억합시다. 이렇게 하려면 그림을 살펴보겠습니다. 차트에는 양수 x와 음수 x 모두에 대해 감소하는 극값이 있습니다. 분명히 숫자 A를 점진적으로 줄이면 1978년 등을 포함하여 필요한 만큼의 근을 얻을 수 있습니다.
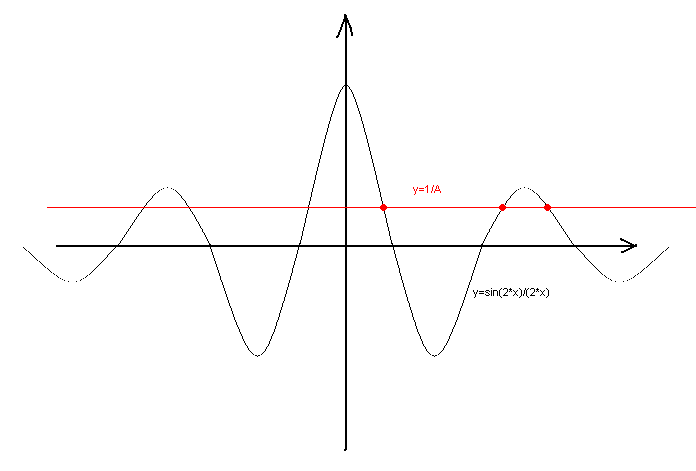
얻은 뿌리는 다르며 순전히 비합리적으로 서로 관련되어 있습니다. 이 경우의 제곱이 쌍으로 같지 않다는 것을 자세히 증명할 필요는 없다고 생각합니다.