F(x,y) = min( x, y + 1/x, 1/y )이라고 하면 F(1/y, 1/x) = 최소( 1/y, 1/x + y, x ) = F(x,y). 따라서 최소값은 y를 1/x로, x를 1/y로 바꾸면 변경되지 않습니다. 예, y = 1/x입니다. 따라서 F(x,1/x) = min( x, 2/x, x ) = min( x, 2/x )입니다. x < sqrt(2)이면 x와 같고 그렇지 않으면 2/x입니다. 두 곡선 y=x 및 y=2/x를 모두 그립니다. 분명히 최대값은 정확히 교차점에 있으며 sqrt(2)와 같습니다. 문제 책의 솔루션은 어쩐지 흐릿하고 마음에 들지 않습니다.
다음(8일): 이 부분은 사소하게 구성되어 있습니다. 음모를 떠나자. 작업의 두 번째 부분(또한 8번째 부분):
아직 방법을 찾지 못했습니다. 나는 생각할 것이다. - 간단히 말해서 아이디어는 이랬습니다. 4각형의 면적은 큰 삼각형 면적과 4개의 작은 삼각형 면적 차이의 1/3, 즉 4제곱센티미터입니다. 큰 삼각형 의 면적을 찾으려면 측면을 찾아야합니다 (그림-A). 정삼각형의 변 을 면적으로 구하는 것은 정삼각형이라는 것을 아는 것은 문제가 되지 않으며 sqr(4*S/sqr(3))과 같습니다.
F(1/y, 1/x) = 최소( 1/y, 1/x + y, x ) = F(x,y).
따라서 최소값은 y를 1/x로, x를 1/y로 바꾸면 변경되지 않습니다. 예, y = 1/x입니다.
따라서 F(x,1/x) = min( x, 2/x, x ) = min( x, 2/x )입니다. x < sqrt(2)이면 x와 같고 그렇지 않으면 2/x입니다.
두 곡선 y=x 및 y=2/x를 모두 그립니다. 분명히 최대값은 정확히 교차점에 있으며 sqrt(2)와 같습니다.
문제 책의 솔루션은 어쩐지 흐릿하고 마음에 들지 않습니다.
다음(8일):
이 부분은 사소하게 구성되어 있습니다. 음모를 떠나자.
작업의 두 번째 부분(또한 8번째 부분):
그림을 단순화하십시오.
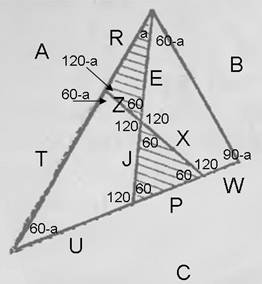
Richie , 음, 음영 처리된 삼각형의 등각은 어디에서 왔습니까?
그건 그렇고, 문제의 조건에서 원래 삼각형이 정삼각형이라는 사실에 대해서는 아무 말도 없습니다. 등변과 유사하게 그려지지만.
어서 해봐요. 입증하다.
-
간단히 말해서 아이디어는 이랬습니다.
4각형의 면적은 큰 삼각형 면적과 4개의 작은 삼각형 면적 차이의 1/3, 즉 4제곱센티미터입니다.
큰 삼각형 의 면적을 찾으려면 측면을 찾아야합니다 (그림-A).
정삼각형의 변 을 면적으로 구하는 것은 정삼각형이라는 것을 아는 것은 문제가 되지 않으며 sqr(4*S/sqr(3))과 같습니다.
В центральном? Это очевидно.
세 삼각형(중앙 삼각형 제외)이 동일한 경우에만그러나 이것은 사실이 아니다.
붙잡을 무언가가 있어야 합니다. 단서가 하나 있지만 아직 그걸로 무엇을 해야할지 모르겠습니다.
세 삼각형(중앙 삼각형 제외)이 동일한 경우에만
그러나 이것은 사실이 아니다.
글쎄, 당신은 나를 완전히 혼란 시켰습니다.
나는 큰 삼각형이 정삼각형이라고 생각했습니다. 작은 3개의 삼각형은 크기가 같으므로 결과적으로 비슷합니다.