記事"R で 統計分布を MQL5 に -"についてのディスカッション - ページ 19 1...121314151617181920 新しいコメント Aleksey Nikolayev 2019.10.22 08:54 #181 Aleksey Nikolayev: Kolmogorov分布を ライブラリに加えたいという要望があります。コルモゴロフ・スミルノフ基準やランダム過程の分解を探索する問題で使われるので、非常に便利です。 念のためここに残しておく。両側1標本検定のKolmogorov-Smirnov統計量の分布のCDFの計算とその追加。 ファイル: KS.mqh 16 kb Aleksey Nikolayev 2019.11.10 18:34 #182 誰かこれを使ったことがある? Renat Fatkhullin 2020.01.29 10:13 #183 Aleksey Nikolayev:MathCumulativeDistributionHypergeometric() 関数で、超幾何分布の CDF が正しく計算されない。定義上、確率分布関数は任意の実数に対して定義されなければならない。以下はmql5上のスクリプトとその結果、そして比較のためにR上でも同じ結果を示しています。結果-1.0 nan 20.0 0.0 00.5 ナノ 2'Hypergeometric.mqh'のゼロ除算 (241,35)結果[1] 0.0000000 0.0000000 0.0000000 0.2222222 あなたは間違った引数を渡し、ERR_ARGUMENTS_INVALID (2)を得ました。入力パラメータを 詳しくチェックしていますが、Rは答えをゼロに置き換えているようです。 //+------------------------------------------------------------------+ //| 超幾何累積分布関数(CDF) //+------------------------------------------------------------------+ //| この関数は、あるオブザベーションが|0|である確率を返す。 //| パラメータm,n,kを持つ超幾何分布から //| はx以下である。| //|| //| 引数:| //| x :希望のオブジェクト数 //| m :母集団の大きさ //| k : 目的の特性を持つアイテムの数 //|| 母集団における| //| n :サンプル数 //| tail :下尾を計算するフラグ //| log_mode : 対数モード。 //| error_code : エラーコードを表す変数。 //|| //| 返り値:| //| ハイパージオメトリック累積分布関数の値。 //| パラメータm,n,kで、xで評価される。 //+------------------------------------------------------------------+ //| ジョン・ブルカートのアルゴリズムに基づく| //+------------------------------------------------------------------+ double MathCumulativeDistributionHypergeometric(const double x,const double m,const double k,const double n,const bool tail,const bool log_mode,int &error_code) { //--- NaNのチェック if(!MathIsValidNumber(x) || !MathIsValidNumber(m) || !MathIsValidNumber(k) || !MathIsValidNumber(n)) { error_code=ERR_ARGUMENTS_NAN; return QNaN; } //--- m,k,n,x は整数でなければならない。 if(m!=MathRound(m) || k!=MathRound(k) || n!=MathRound(n) || x!=MathRound(x)) { error_code=ERR_ARGUMENTS_INVALID; return QNaN; } //--- m,k,n,xは正でなければならない。 if(m<0 || k<0 || n<0 || x<0) { error_code=ERR_ARGUMENTS_INVALID; return QNaN; } //--- 範囲をチェックする if(n>m || k>m) { error_code=ERR_ARGUMENTS_INVALID; return QNaN; } Renat Fatkhullin 2020.01.29 10:31 #184 Aleksey Nikolayev:例えば、二項係数の中には負のものもある(すべてではない):結果: -309196571788882235本来は: 349615716557887488 K (28) が大きいため、64 ビット long がそこでオーバーフローした。戻り値は longである。 このような制限内で値をカウントするには、関数をダブル値に書き換える必要があります。 Aleksey Nikolayev 2020.01.29 10:35 #185 Renat Fatkhullin:不正な引数を渡したため、ERR_ARGUMENTS_INVALID (2)が発生しました。入力パラメータを 詳しくチェック すると、Rは答えをゼロに置き換えているようです。 1) どんなCDF - 確率分布関数(離散的なものも例外ではありません!)も、すべての実数に対して定義されなければなりません。以下はRのコードとその結果のアナログで、これが現実にどのようにカウントされるべきかを示している。ところで、離散CDF関数には正しくカウントされるものとされないものがある。 2) 値1の場合、ゼロによる除算エラーが発生する。 Renat Fatkhullin 2020.01.29 10:52 #186 Aleksey Nikolayev:1) どのようなCDF-確率分布関数(離散的なものも例外ではありません!)も、すべての実数について定義されなければなりません。以下は、Rのコードとその結果のアナログで、これが現実にどのように考慮されるべきかを示している。ところで、離散CDF関数には、正しく数えられたものとそうでないものがある。2) 値1の場合、ゼロによる除算エラーが発生する。 関数のコードとそのチェックを読んでください。 手元にRがないので、別途チェックする必要がある。ゼロによる除算を 見ると、境界条件を理解する必要があります。 Aleksey Nikolayev 2020.01.29 11:22 #187 Renat Fatkhullin:K(28)が大きいため、64ビットのlongがそこでオーバーフローした。戻り 値はlongである。このような制限内で値をカウントするには、関数をダブル値に書き換える必要がある。 それは明らかである。ただ、整数の引数で二項係数の対数のエラーがあり、それが原因だと思っていました。今、コードを見て、私が間違っていたことに気づきました。 #include <Math\Stat\Math.mqh> void OnStart() { Print(MathBinomialCoefficientLog(62,28)); Print(MathBinomialCoefficientLog(62.0,28.0)); } 結果は test_clog (EURUSD.m,MN1) -nan(ind) test_clog (EURUSD.m,MN1) 40.39561099351077 追記 誤り。問題はオーバーフローにもある。 Aleksey Nikolayev 2020.01.29 11:27 #188 Renat Fatkhullin:手元にRはない、 オンラインR compile R online rextester.com compile R online Denis Kirichenko 2024.07.20 00:21 #189 NoncentralBetaのトラブル。ドキュメントから スクリプトを引用した。 パラメータを変えた場合の結果です。 Документация по MQL5: Стандартная библиотека / Математика / Статистика / Нецентральное бета-распределение www.mql5.com В данном разделе представлены функции для работы с нецентральным бета-распределением. Они позволяют производить расчет плотности, вероятности... Denis Kirichenko 2024.07.20 00:33 #190 ドキュメントの 数式: ウィキペディアの類語: コードを見てみた。 MathRandomNoncentralBeta() 関数にはこのような行がある: //--- 非心カイ二乗を用いて乱数を生成する。 double chi1=MathRandomNoncentralChiSquare(a2,lambda2,error_code); double chi2=MathRandomNoncentralChiSquare(b2,lambda2,error_code); result[i]=chi1/(chi1+chi2); 同じウィキペディアにはこうある: The noncentral beta distribution (Type I) is the distribution of the ratio ここで は自由度 m と 非心 パラメータ ↪Ll_1D706 を持つ非心カイ2乗 確率 変数で 𝜒 𝑛 2 は 、 𝜒 2 ( ↪Ll_1D712 ) から独立な自由度 n を持つ 中心カイ2乗 確率 変数 です。 つまり、2つの確率変数が取られ、1つ目は非心カイ2乗分布から、2つ目は中心分布から 取られます。おそらく、このコードは修正可能であろう: //--- 非心カイ二乗を用いて乱数を生成する。 double chi1=MathRandomNoncentralChiSquare(a2,lambda2,error_code); double chi2=MathRandomChiSquare(b2,error_code); result[i]=chi1/(chi1+chi2); 例のグラフを修正したものが以下になります。 Документация по MQL5: Стандартная библиотека / Математика / Статистика / Нецентральное бета-распределение www.mql5.com В данном разделе представлены функции для работы с нецентральным бета-распределением. Они позволяют производить расчет плотности, вероятности... 1...121314151617181920 新しいコメント 取引の機会を逃しています。 無料取引アプリ 8千を超えるシグナルをコピー 金融ニュースで金融マーケットを探索 新規登録 ログイン スペースを含まないラテン文字 このメールにパスワードが送信されます エラーが発生しました Googleでログイン WebサイトポリシーおよびMQL5.COM利用規約に同意します。 新規登録 MQL5.com WebサイトへのログインにCookieの使用を許可します。 ログインするには、ブラウザで必要な設定を有効にしてください。 ログイン/パスワードをお忘れですか? Googleでログイン
Kolmogorov分布を ライブラリに加えたいという要望があります。コルモゴロフ・スミルノフ基準やランダム過程の分解を探索する問題で使われるので、非常に便利です。
念のためここに残しておく。両側1標本検定のKolmogorov-Smirnov統計量の分布のCDFの計算とその追加。
MathCumulativeDistributionHypergeometric() 関数で、超幾何分布の CDF が正しく計算されない。定義上、確率分布関数は任意の実数に対して定義されなければならない。以下はmql5上のスクリプトとその結果、そして比較のためにR上でも同じ結果を示しています。
結果
-1.0 nan 2
0.0 0.0 0
0.5 ナノ 2
'Hypergeometric.mqh'のゼロ除算 (241,35)
結果
[1] 0.0000000 0.0000000 0.0000000 0.2222222
あなたは間違った引数を渡し、ERR_ARGUMENTS_INVALID (2)を得ました。入力パラメータを 詳しくチェックしていますが、Rは答えをゼロに置き換えているようです。
例えば、二項係数の中には負のものもある(すべてではない):
結果: -309196571788882235
本来は: 349615716557887488
K (28) が大きいため、64 ビット long がそこでオーバーフローした。戻り値は longである。
このような制限内で値をカウントするには、関数をダブル値に書き換える必要があります。
不正な引数を渡したため、ERR_ARGUMENTS_INVALID (2)が発生しました。入力パラメータを 詳しくチェック すると、Rは答えをゼロに置き換えているようです。
1) どんなCDF - 確率分布関数(離散的なものも例外ではありません!)も、すべての実数に対して定義されなければなりません。以下はRのコードとその結果のアナログで、これが現実にどのようにカウントされるべきかを示している。ところで、離散CDF関数には正しくカウントされるものとされないものがある。
2) 値1の場合、ゼロによる除算エラーが発生する。
1) どのようなCDF-確率分布関数(離散的なものも例外ではありません!)も、すべての実数について定義されなければなりません。以下は、Rのコードとその結果のアナログで、これが現実にどのように考慮されるべきかを示している。ところで、離散CDF関数には、正しく数えられたものとそうでないものがある。
2) 値1の場合、ゼロによる除算エラーが発生する。
関数のコードとそのチェックを読んでください。
手元にRがないので、別途チェックする必要がある。ゼロによる除算を 見ると、境界条件を理解する必要があります。
K(28)が大きいため、64ビットのlongがそこでオーバーフローした。戻り 値はlongである。
このような制限内で値をカウントするには、関数をダブル値に書き換える必要がある。
それは明らかである。ただ、整数の引数で二項係数の対数のエラーがあり、それが原因だと思っていました。今、コードを見て、私が間違っていたことに気づきました。
結果は
test_clog (EURUSD.m,MN1) -nan(ind)
test_clog (EURUSD.m,MN1) 40.39561099351077
追記 誤り。問題はオーバーフローにもある。
手元にRはない、
オンラインR
NoncentralBetaのトラブル。ドキュメントから スクリプトを引用した。
パラメータを変えた場合の結果です。
ドキュメントの 数式:
ウィキペディアの類語:
コードを見てみた。
MathRandomNoncentralBeta() 関数にはこのような行がある:
同じウィキペディアにはこうある:
The noncentral beta distribution (Type I) is the distribution of the ratio
ここで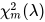 は自由度 m と 非心 パラメータ ↪Ll_1D706 を持つ非心カイ2乗 確率 変数で 𝜒 𝑛 2 は 、 𝜒 2 ( ↪Ll_1D712 ) から独立な自由度 n を持つ 中心カイ2乗 確率 変数 です。
は自由度 m と 非心 パラメータ ↪Ll_1D706 を持つ非心カイ2乗 確率 変数で 𝜒 𝑛 2 は 、 𝜒 2 ( ↪Ll_1D712 ) から独立な自由度 n を持つ 中心カイ2乗 確率 変数 です。
つまり、2つの確率変数が取られ、1つ目は非心カイ2乗分布から、2つ目は中心分布から 取られます。おそらく、このコードは修正可能であろう:
例のグラフを修正したものが以下になります。