記事「パターン検索への総当たり攻撃アプローチ（第VI部）：循環最適化」についてのディスカッション

[MetaQuotes]

新しい記事「パターン検索への総当たり攻撃アプローチ（第VI部）：循環最適化」はパブリッシュされました:

この記事では、MetaTrader 4および5の取引の自動化チェーン全体を完成するだけでなく、より興味深いことができるようになった改善の最初の部分を示します。今後、このソリューションにより、EAの作成と最適化の両方を完全に自動化し、効果的な取引構成を見つけるための人件費を最小限に抑えることができます。

アイデア全体の中で最も重要な要素は、端末とプログラム間の対話システムです。実際、これは高度な最適化基準を備えた循環オプティマイザーです。最も重要なものについては前のセクションで説明しました。システム全体が機能するためには、まず、MetaTrader 5端末の1つであるクオートのソースが必要です。前回の記事ですでに示したように、クオートは私にとって都合の良い形式でファイルに書き込まれます。これはEAを使用しておこなわれますが、一見するとかなり奇妙に機能します。

EAの機能に独自のスキームを使用することは、非常に興味深く有益な経験であることがわかりました。ここでは私が解決する必要があった問題のデモンストレーションにすぎませんが、これらはすべてEAの取引にも使用できます。

 

作者: Evgeniy Ilin

[fxsaber]

формулы 2

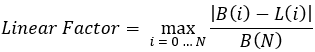
この計算式の中身を理解しよう：

• N - バックテストまたは取引セクション全体を通して、完全にオープンおよびクローズされた取引ポジションの数。
• B(i) - 対応するクローズポジション「i」の後のバランスラインの値。
• L(i) - ゼロから直近の残高ポイント（最終残高）まで引いた線。

ほぼシャープと 思われる：

//--- エクイメント配列からインクリメントの対数を計算する。
   for(int i = 1; i < m_bars_counter; i++)
     {
      //--- エクイティが変更された場合のみ追加
      if(m_equities[i] != prev_equity)
        {
         log_return = MathLog(m_equities[i] / prev_equity); // インクリメントの対数
         aver += log_return;            // インクリメントの平均対数
         AddReturn(log_return);         // インクリメントから対数の配列を埋める
         counter++;                     // 収穫カウンター
        }
      prev_equity = m_equities[i];
     }
//--- シャープレシオを計算するのに十分な値がない場合は、0を返す。
   if(counter <= 1)
      return(0);
//--- 増分の対数の平均値
   aver /= counter;
//--- 標準偏差を計算する
   for(int i = 0; i < counter; i++)
      std += (m_returns[i] - aver) * (m_returns[i] - aver);
   std /= counter;
   std = MathSqrt(std);
//--- 現在のタイムフレームにおけるシャープレシオ
   double sharpe = aver / std;

[Evgeniy Ilin]

fxsaber #:

ほとんどシャープ だと思う：

似たようなものはあるが、一見しただけだ。誰もがバランスシートの成長モデルを見逃している。残高の伸びの傾きが常に落ちている（残高曲線の二次導関数がマイナス）場合、すぐにマイナスになる可能性があるので、そのようなモデルは好ましくない。要は、図式的に最も有望に見える曲線を選択することである。

[fxsaber]

Evgeniy Ilin #:

類似点はあるが、一見しただけ。誰もがバランス成長のモデルを見逃す。バランス成長の傾きが常に下がっている（バランス曲線の2階微分がマイナス）場合、すぐにマイナス領域に入る可能性があるため、そのようなモデルは好ましくない。要は、図式的に最も有望に見える曲線を選ぶことである。

下降曲線に対するシャープ・アルゴリズムは負の値を与える。シャープについて議論する意味はない。

私の経験からの例

• 基準「美しい曲線」 - OOSに合格しない。
• 醜い曲線」という基準 - OOSに合格するが、曲線自体は美しいことが判明した。
• 手数料ゼロ - OOSに合格しない。
• 手数料が設定されている - OOSに合格。

つまり、最適化が美しさのためである場合、フィッティング成分が高いことが判明した。価値あるものが見つかれば、それは美しく見える。

だから私自身は美しさを追求しない。それよりもTSコアのディール数とアルゴリズムに頼っている。目標は、美しさの基準なしに美しさを得ること だ。原則として、このバリアントはOOSをパスする。

ZY 手数料のあるバリアントはより興味深い（しかし、原則として逆もある：手数料が少ないほど、パターンを見つける確率が高くなる）。実際に取引回数は減りますが（統計的有意性）、検索が成功する確率は高くなります。

[Evgeniy Ilin]

fxsaber #:

下降カーブに対するシャープ・アルゴリズムは負の値を出す。これは単なる類推であり、シャープについて議論する意味はない......。

私の経験からの例

• 美しい曲線」という基準 - OOSは通らない。
• 「醜いカーブ」基準 - OOSに合格するが、カーブ自体は美しい。
• ゼロ・コミッション - OOSに合格しない。
• コミッションセット - OOSに合格。

つまり、最適化が美しさを追求する場合、フィッティングの要素が高いことがわかる。価値あるものが見つかれば、それは美しく見える。

だから私自身は美しさを追求しない。それよりもTSコアのディール数とアルゴリズムに頼っている。目標は、美しさの基準なしに美しさを得ること だ。原則として、このバリアントはOOSをパスする。

ZY 手数料のあるバリアントはより興味深い（しかし、原則として逆もある：手数料が少ないほどパターンを見つける確率が高くなる）。実際に取引回数は減りますが（統計的有意性）、検索が成功する確率は高くなります。

それでもまだ限界があることは明らかだ。例えば、私はこうしている：

• 最低必要期待値をpipsで設定する（スプレッドを考慮し、手数料とスワップも加える）。
• 最低必要取引回数を設定し、検討区間の長さを考慮します。
• カーブマッチングファクターを調整する

スプレッドの内側で何かを探す意味はない。）それは事実であり、それでできることは何もない。フィッティングはどこにでもある。問題は、アルゴリズム自体に注意を払うことなく、それを最小限に抑える方法である。方法はある。ただ、カーブの見積もりなしで、アルゴリズムが最初はgraalであるという事実を頼りにすることができます。 私はそれなしで行う方法のメソッドを持っていますが、私はここでそのようなことを書くことを恐れています））。

[fxsaber]

Evgeniy Ilin #:

まだ限界があるのは明らかだ。これが私のやり方だ：

• 私は、最低限必要なマットの期待値をポイントで設定します（スプレッドを考慮するだけで、手数料とスワップもおおよそ加算します）。

私はそんなことはしません。市場の規則性はブローカーの取引条件に左右されない。私はこれに傾いている。

取引、自動取引システム、取引戦略のテストに関するフォーラム

トレーディングにおける機械学習：理論、パターン、実践とアルゴ-トレーディング

fxsaber、2023.08.19 11時10分午前

最も高い潜在的な利益によって選択するための過去のデータのためのブローカー。例えば、EURUSD_Broker1 の潜在的な利益は EURUSD_Broker2 のそれよりも高い。それならEURUSD_Broker1を選ぶ。

メジャーもクロスもスキャルピングできる。しかし、すべてではない。それぞれをトレーニングして結果を見ればいい。これが私のやり方だ。

つまり、「岩の中の金」の濃度が高いところを探すのが理にかなっている。

• そのエリアの長さを考慮して、最低限必要なトレード数を設定するんだ

そう、これは遺伝学にとって、行き止まりの枝に行かないための一種の助けなのだ。

• カーブフィット係数の調整。

それこそわざとやらないことです。例えば、PF>2.5を出すようにTSを訓練することができます。適切なトレード回数があれば、ほぼ自動的に美しいカーブを出すことができます。私はまだあまり実践していません。しかし、研究のためには、もちろんいつ見ても面白い。

スプレッドの内側にあるものを探しても意味がない。）トレードがほとんどないのは事実です。問題は、アルゴリズム自体に注意を払うことなく、それを最小限に抑える方法です。方法はあります。ただ、カーブの推定がなければ、アルゴリズムが最初はgraalであるという事実だけを頼りにすることができます。 私はそれなしで行う方法のメソッドを持っていますが、私はここでそのようなことを書くことを恐れています））。

私はスプレッドにTSの接続を理解していない。

[Evgeniy Ilin]

@fxsaber

• Например, можно обучить ТС, чтобы выдавал PF>2.5. При должном количестве сделок это почти автоматом выдаст красивую кривую

美しいかもしれないが、形が違う、可能な前進は形次第だ。少なくとも、使えるセットアップが見つかる確率は上がる。利益率2.5は太っ腹、1.5でもかなり太っ腹だと思う）フィッティングでこういう数字が出るのは普通。これは、より多くの設定を取捨選択することで、残った設定（私の基準）に重み付けをする方法みたいなものです。私はロボット工学において、主な仕事はアルゴリズムの上のアドオンによって行われ、アルゴリズムにはほとんど依存しないという興味深いパラダイムに一般的に至っている。ここでは、特定のセッティングの重要性を高める基準には価値がある。結局のところ、総体として、それらはそれぞれ独自のレベルで機能する。

私は残りの部分に同意する。

。

• TSとスプレッドの関係がよくわからない。

スキャルピングならそうですが、ここではビッドとすべてを使用し、原則としてアスクはスプレッドから浮いています。しかし、ティックは多くの人にとって異なっており、多くはそれに依存します）。ただポイントは、スプレッドは、我々はそれが例えば、ブローカーを変更するときの信号に影響を与えないようにスプレッドを無視した場合、スプレッドの1つの貿易の平均サイズよりもできるだけ小さく、ポイントであったということです、よく、これは私の空想である）。

[fxsaber]

Evgeniy Ilin #:
それは美しいかもしれないが、形状は異なり、可能な前進は形状に依存する。

美しさではなく）MaxBalance基準で見つけた曲線の例。

[Anatoli Kazharski]

fxsaber #:

MaxBalance基準で見つけた曲線の例（きれいさではない）。

この方法（MaxBalance基準 "美しさによるものではない"）で選択された多くの曲線を見るのは興味深い。

[fxsaber]

Anatoli Kazharski #:

このような方法で多くのカーブが選ばれるのを見るのは面白いだろう（MaxBalanceの基準「美しさによるものではない」）。

これは対応するoptファイルの6番目の結果である。最初の5つはもっと悪く見える。

私は、入力パラメータセットが互いに近くならないように、少数のGAパスを行う。

[fxsaber]

MaxBalance基準に下からの取引回数の 制限を加えると、常にSampleの曲線が美しくなる。この場合、たとえOOSで完全な損失が出たとしても、そのようなTSは合理的なものと考えることができる。しかし、シャープ、R^2、あるいはこの記事の基準によって美しさを求めるのは疑わしいように思われる。もしかしたら、私が間違っているのかもしれない。