私の結果では、系列の確率は0.5^nです。
MAでは同じです
私の結果によると、直列の確率は0.5^nです
は、前回(数千年前)のクリスマスの頃に落ちていたはずです。
ショート」を「ショート」、「ロング」を「ロング」と呼ぶのには理由があります。
株式ではその比率はほぼ良好ですが、FXではかなり不鮮明なはずです。
シリーズの長さは、同値や体の小さい反対側のローソク足で中断されますか?
そうであることは明らかです。
質問は、長いシリーズがドージや反対側のローソク足で中断され、その後、前のシリーズが再び繰り返されることがあるというものでした。
ここに利益はないが、話題はある)
そんな解析で何ができるのか、私にはわからないが、私の不勉強のせいにしておこう。
しかし、分析の本質に関する観察がある。
私の理解では、高さゼロのローソク足は計算から除外されます。最小限の高さ(1、2、3)の燭台は、それらと大きく異なるのでしょうか?あまり変わらないと思います。
有意」な長さのローソク足だけを考慮する方が正しいと思うのですが。重要性の基準として、(O-C)/(H-L)比のモジュラスを取ることができる。
閾値は別途検討する必要がある。
4時系列ではこのような結果になります。
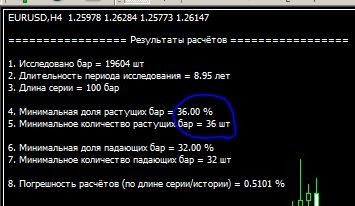
100本の棒グラフのシリーズには、少なくとも36本の立ち上がり棒グラフが必要です。
このことから、50本のバーのシリーズで、すでに10本の上昇バーがあったと結論付けることができます。
であれば、次の50本では、少なくとも36-10=26本の上昇棒がなければなりません(最低でも)。
その結果、そこでの落下バーは50-26=24程度になる。
つまり、下降と上昇のバーの数はほぼ同じになります。
もちろん、バーの高さは考慮されていません。
4時系列ではこのような結果になります。
100本の棒グラフのシリーズには、少なくとも36本の立ち上がり棒グラフが必要です。
このことから、50本のバーのシリーズで、すでに10本の上昇バーがあったと結論付けることができます。
であれば、次の50本では、少なくとも36-10=26本の上昇棒がなければなりません(最低でも)。
その結果、そこでの落下バーは50-26=24程度になる。
つまり、下降と上昇のバーの数はほぼ同じになります。
もちろん、バーの高さは考慮されていません。
このような分析で何ができるのかがつかめない_。
しかし、総合的な要素から恩恵を受けることは十分に可能です。
プロセッサーは何の役に立つのか?唯一無二の存在であれば、なし。しかし、マザーボードやグラフィックカード、電源などを追加すると・・・。- どうなるかわかるだろう。
このフィカスピクスは、価格のデジタル化、つまりピッチを設定したグリッドに変換することで簡単に解消することができます。しかし、それについては後で詳しく説明します。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
このパートでは、バー(ローソク足)シリーズの探索に焦点を当てます。
以下のスクリプトでは、次の用語を使用しています:上昇バーは 始値より 終値が高いバー、下降 バーは始値より終値が低いバーです。
まず始めに、スクリプトを公開します。棒グラフの計算に論理的な間違いがないか、プログラミングのプロにチェックしてもらうんです。計算のロジックに間違いがあれば-。
ご意見をお聞かせください。
このスクリプトは、与えられた長さの系列において、増加するバーと減少するバーの最小 シェアを計算します。シリーズの長さはソースデータのウィンドウで設定され、デフォルトで100本のバーとして指定されています。
スクリプトの動作結果は、スクリプト起動後しばらくしてチャートに表示されます。例えば、EURUSD TF H1 の 100 本のバーのシリーズでは、最小の 歴史的 増加するバーの数は
バー34本(34%)。
注意したいのは、スクリプトは履歴全体を実行するので、履歴が長い(TFが小さい)か、系列が大きい(100以上)場合、スクリプトは
は、最大で数分間(PCの性能に依存)、十分な計算を行うことができます。
スクリプトです。
また、このスクリプトはゼロバー(始値と終値が等しいバー)を考慮に入れていない点にもご注目ください。もし、このスクリプトの計算に対する批判や、類似の研究分野での成果などがあれば、ぜひ発言してください。
後ほど、一連のバーに関する規則性の議論と、このトピックに関連するいくつかのタスクに参加する予定です。