ソースから始めなければならない
リンクしないでください。さもないと、ほとんど誰もあなたが達成しようとしていることを本当に理解していない、別のEconometrics 2スレッドが存在することになります。自分の言葉で、faa!
最近、厚い尾は外れ値、多くは単一外れ値によって引き起こされるという記事を読みました。違う意見もあったと記憶しています。でも、間違っているかもしれませんね。
行き方は?何もないところから、掲示板の人たちのあからさまな無知と戦いながら。ドン・キホーテここには、何も読まないことを誇りにしている人がたくさんいます。ひどすぎる! そして、ここで一気に2つのリンクを紹介します。
いいえ、オリジナルのみ議論可能です。現代の発言」は認めない
正確に表現できていなかったかもしれません。リンクは完全に原型をとどめており、より広くなっている可能性があります。でも、そんなことはどうでもいいんです。
余談ですが
プログラミング言語の演算 子のセマンティクスとは何ですか?その演算子を実行するのは、プログラム、つまりコードです。
ARMAモデルとは?これは、そのモデルを実行するコードです。
この解釈から離れると、リテラシーの高い人たちの異なる解釈や、無知な人たちの用語レベルでの過剰な解釈に溺れることになるのです。
このフォーラムでは - プログラム(実行可能コード)はセマンティクスです。つまり、Boxの本のセマンティクスは、STATISTICSのように、トレーディングの公式、言葉に価値ある意味を与えるプログラムなのです。
では、はじめましょう。
ARIMAモデルは、次のような形式で記述される。ARIMA (p,d,q) または AR(p) I(d) MA(q), ここでpとqは回帰式のラグ数、dは元の系列を微分した回数である。
まず、ARMAをとり、ラグ数を選択する。2011.11.28 00:00 から 2011.12.23 21:00 までのEURUSDを取り上げます。これは整数の週数で、各週は118時間のバー、つまり全472本のバーがあります。
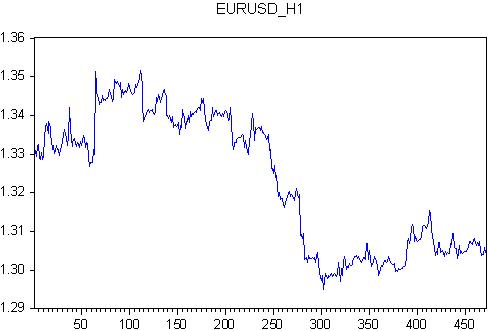
この引用文のために、正規表現式を書きます。
EURUSD AR(1) MA(1) C @trend
すなわち、自己回帰、誤差、シフト(定数)、線形トレンドによってEURUSD商を定義します。
この回帰の係数を推定してみよう。

2つのパラメータではまずまずの結果が得られ、残りの2つのパラメータでは横ばいの結果が得られています。trend ma(1)は係数を推定する際に非常に大きな誤差の値を持つ。
この演習の実用的な成果は何でしょうか?
(1) 数値で特性を表す指標としてプログラム可能な方程式がある。
(2) 本指標では、商の前回値と回帰値との差分のみを考慮する。だから、私たちの指標はより正確なのです。
(3) TAの全く新しい結果:指標の係数は確率変数である。少なくとも一つの結論は、現在の引用に係数を適応させない指標は意味がない、ということです。
.....
(2) 本指標では、商の前回値と回帰値との差分のみを考慮する。だから、私たちの指標はより正確なのです。
(3) TAの全く新しい結果:指標の係数は確率変数である。少なくとも一つの結論は、現在の相場に対する比率の適応を伴わない指標は無意味である、ということだ。
(2) 何より正確なのは?
(3) 指標の精度が上がっても、意味がないのでは?
(2) 何より正確なのは?
(3) インジケータの精度が上がっても意味がないのは、何のため?
自己満足にしか興味がないのでしょう。
計量経済学は 利益のためではなく、世界の危機のためにある。
どの指標がより正確であるかは問題ではなく、無意味であることも問題ではありません。オタクにとって一番大切なことは、手元に来たものをすべて計算することです。しかし、プログラマーはやっとEViewsをマスターして、プログラムにデータを突っ込んで、意味のない数字が返ってくることに満足している。ここで重要なのは、結果ではなく、そのプロセスの楽しさなのです。
経済学者は、私たちが一緒に喜ぶことを望んでいるのです。だから、重商主義で彼の機嫌を損ねたり、計量経済学の無意味な可能性を喜んだりするのはやめよう。
また、世界危機を引き起こしたジェンキンスとボックスの記憶に敬意を表し、1分間の黙祷を捧げよう。つまり、彼らに悪態をつかずに1分間を過ごすことを心がけよう。すぐに実現できるわけでもなく、誰にでもできるわけでもありませんが、やってみるしかないのです。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
今から38年前の1974年、ボックスとジェンキンスによる伝説の名著「時系列解析」が出版された。本書は、時系列分析や予測に大きな影響を与え、今も与え続けている。現在でも、アメリカの政府機関は、新しいものがたくさん出てきたとはいえ、このモデルを改変して予測を行っている。でも、ベテラン勢のことは忘れないようにしましょう。
本書では、ARMA モデル、 ロシア語訳ARSSまたはARPSSのARIMAを 紹介しています。
このモデルについては、いろいろと誤解があるようです。まずは名前から。
ロシア語では、ARSS - 自己回帰と移動平均。
AR - autoregressive - は自明である。時系列の最後の項は、その前のラグされた値を通して定義される。ほぼすべての指標に共通する考え方。
SS - 移動平均。ここが厄介なんです。体重計とは関係ないんです。それは、ノイズのモデリングについてです。すなわち、モデルは当初、APで記述される決定論的なものと、MAで記述されるノイズという2つの要素から市場を表現する。指標としては、これは明らかに1974年以降の新しい言葉です
ARSSモデルを拡張したARPSSという形式があり、ここでPはプロインテグレートである。そこで登場するのが統合とは差別化のことですつまり、商の隣り合った棒の差を取ったのだ!
そして、ボックスとジェンキンスの最後の功績。BPの非定常性が明示的に認識され、非定常時系列を定常時系列に変換する方法が提案されている。P」はまさに非定常のVRを定常に変換する方法です。
このモデルで計算した結果は、このトピックの中でさらに紹介します。その結果とForaへの適用性を議論することを提案します。このモデルについては、STATISTICSのドキュメントとソフトウェアの実装の両方で十分に議論されています。この件に関しては、STATISTICSに劣るようですが、EViewsを使うことにします。
では、はじめましょう。