Если приращения случайны, то цена - это random walk, она имеет нормальное распределения, и заработать на ней гарантированно нельзя. Однако надо оговорить природу приращения, сказать просто "случайная" - не сказать ничего. В жизни всё случайно. У автобуса есть расписание, но время его прибытия величина случайная. Случайные приращения цены могут быть коррелированы с фазами луны, например, это не делает их неслучайными. Чтобы получить random walk приращения должны быть iid независимыми и одинаково распределёнными.
Приращение цены можно считать нормально распределённым - это достаточно близко к реальности, однако это ничего не даст, если оно iid . Можно считать приращение цены t-распределённым со степенью свободы 4 или 5. Это гораздо ближе к реальности, чем допущение о нормальности приращений. Результирующий процесс будет random walk. Вот он-то вообще гарантированно нормально распределённый, независимо от распределения приращений, но от той нормальности никакого прока - нельзя заработать на случайном блуждании. Приращение цены можно считать стационарными, но их нельзя торговать. Торговать можно цену, а она random walk, процесс нестационарный. По крайней мере в контексте данного топика.
Можно я для поддержания дискуссии немножко поспорю? Я сейчас сам не очень уверен в том, что хочу сказать. Тем более уже очень поздно. Но все-таки... Если приращения какой-то величины нормально распределены, то это значит, что эта величина ограничена. (Ошибаюсь?)
Если не ошибся в предыдущем утверждении, то во множестве значений величины есть максимумальное и минимальное. Кроме того, чем ближе значение величины к максимальному или минимальному, тем больше вероятность его изменения в сторону среднего. Вот это и есть закон, который можно использовать.
п.с. Не подумайте, что я нападаю. Просто хочу поговорить с умным человеком.
Можно я для поддержания дискуссии немножко поспорю? Я сейчас сам не очень уверен в том, что хочу сказать. Тем более уже очень поздно. Но все-таки... Если приращения какой-то величины нормально распределены, то это значит, что эта величина ограничена. (Ошибаюсь?)
Если не ошибся в предыдущем утверждении, то во множестве значений величины есть максимумальное и минимальное. Кроме того, чем ближе значение величины к максимальному или минимальному, тем больше вероятность его изменения в сторону среднего. Вот это и есть закон, который можно использовать.
п.с. Не подумайте, что я нападаю. Просто хочу поговорить с умным человеком.
На тебе гистограмму и пробабилити плот для 1000-го отсчёта.
Хотя исходя из того, что приращения были нормальные, сумма нормальных распределений есть нормальное распределение. Тут ничего даже и проверять-то не надо.
Если приращения случайны, то цена - это random walk, она имеет нормальное распределения, и заработать на ней гарантированно нельзя.
Однако надо оговорить природу приращения, сказать просто "случайная" - не сказать ничего. В жизни всё случайно. У автобуса есть расписание, но время его прибытия величина случайная. Случайные приращения цены могут быть коррелированы с фазами луны, например, это не делает их неслучайными.
Чтобы получить random walk приращения должны быть iid независимыми и одинаково распределёнными.
それは、価格の増分が正規分布していないことです。そうでなければ、それで儲かることが保証されているのですから。
В том то и дело, что приращение цены не нормально распределено. Иначе заработать на нем было бы гарантированно можно.
異常な増分は何に対してのものですか?
В том то и дело, что приращение цены не нормально распределено. Иначе заработать на нем было бы гарантированно можно.
価格増分は正規分布と仮定できるので現実に近いが、iid であれば何もしない。価格増分は、自由度4または5のt分布と考えることができる。これは、増分が正常であると仮定するよりも、はるかに現実に近いものです。
その結果、ランダムウォークとなる。増分の分布に関係なく正規分布することが保証されていますが、正規性は役に立ちません - ランダムウォークで儲けることはできないのです。価格差は定常的なものと考えることができますが、取引することはできません。価格を取引することができ、それはランダムウォーク、非定常過程である。少なくとも、このトピックの文脈では。
Приращение цены можно считать нормально распределённым - это достаточно близко к реальности, однако это ничего не даст, если оно iid . Можно считать приращение цены t-распределённым со степенью свободы 4 или 5. Это гораздо ближе к реальности, чем допущение о нормальности приращений.
Результирующий процесс будет random walk. Вот он-то вообще гарантированно нормально распределённый, независимо от распределения приращений, но от той нормальности никакого прока - нельзя заработать на случайном блуждании. Приращение цены можно считать стационарными, но их нельзя торговать. Торговать можно цену, а она random walk, процесс нестационарный. По крайней мере в контексте данного топика.
議論を続けるために、少し反論してもいいですか? 今、何を言いたいのかよくわからないんです。特に今はとても遅いです。それにしても...ある量の増分が正規分布であれば、この量は有界であることを意味する。(私が間違っているのか?)。
前述が間違いでない限り、ある量の値の集合には最大値と最小値が存在する。また、最大値や最小値に近い値ほど、平均値に向かって変化しやすい。これが使える法律です。
p.s. 私が攻撃していると思わないでください。ただ、知的な人と会話をしたいだけです。
Можно я для поддержания дискуссии немножко поспорю? Я сейчас сам не очень уверен в том, что хочу сказать. Тем более уже очень поздно. Но все-таки... Если приращения какой-то величины нормально распределены, то это значит, что эта величина ограничена. (Ошибаюсь?)
Если не ошибся в предыдущем утверждении, то во множестве значений величины есть максимумальное и минимальное. Кроме того, чем ближе значение величины к максимальному или минимальному, тем больше вероятность его изменения в сторону среднего. Вот это и есть закон, который можно использовать.
п.с. Не подумайте, что я нападаю. Просто хочу поговорить с умным человеком.
アークサイン定理とプレイヤーエラーについてご存じないのでしょうか?
無駄に偏向の相対性理論を聞いたわけではありません。
戻ってきたら-1曲。
MA(x期)は別曲ですが...。
MAではなくTrueDMAを使えば、まったく違うカカフォニーを奏でることができるのです。
;)
どこでアブノーマルを手に入れたのか?
誰にも聞くな、何も言わん。
トピックが あります。それは、逆のことを示すのです。
ヨー・マイ・・・。
:)
Можно я для поддержания дискуссии немножко поспорю? Я сейчас сам не очень уверен в том, что хочу сказать. Тем более уже очень поздно. Но все-таки... Если приращения какой-то величины нормально распределены, то это значит, что эта величина ограничена. (Ошибаюсь?)
Если не ошибся в предыдущем утверждении, то во множестве значений величины есть максимумальное и минимальное. Кроме того, чем ближе значение величины к максимальному или минимальному, тем больше вероятность его изменения в сторону среднего. Вот это и есть закон, который можно использовать.
п.с. Не подумайте, что я нападаю. Просто хочу поговорить с умным человеком.
絶対に間違っています。分布の性質は、価値の制限について何も語っていない。例外もあるだろうが、一般的にはそうである。 分布のパラメータによって制限を受ける。例:正規分布の有病率は〜N(0,1)である。定常的なプロセスで、マグニチュードの限界があり、4や-4にはほとんど達しない。
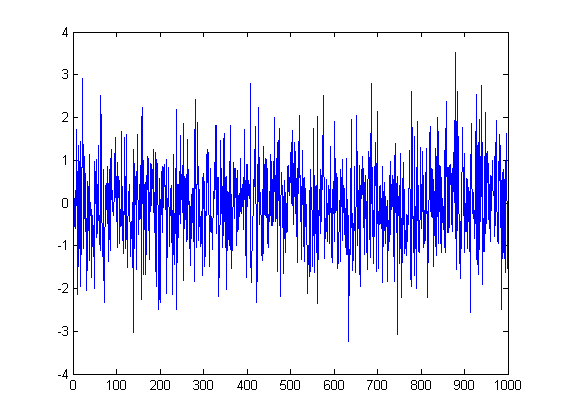
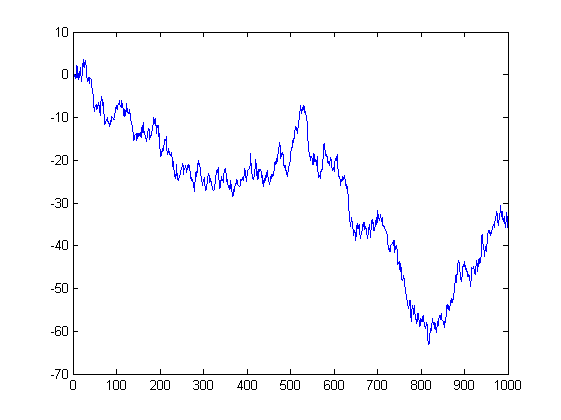

そして、その刻みで出てくる価格がこちらです。ランダムウォークなんです。これも正規分布 ~N(0,sigma^2) を持ちますが、その分散パラメータは一定ではなく、時間、つまり増分値とともに増加します。当然、このプロセスにはサイズ制限がなく、すべてのポイントを等確率で訪問する。これがギャンブラー破産問題の基本です。完全に公平なゲーム(50:50)で長くプレイしても、遅かれ早かれこの曲線は、あなたが持っているお金より低く導くので、あなたはまだ負けるでしょう。
そして、ここに1,000個のランダムなさまがあります。明らかに正規分布のベルが見えますね。
しかし、平均に戻るというのは別の話で、平均回帰のプロセス、つまり自己回帰(AR)なのです
x(i) = a * x(i-1) + e(i) となります。e(i)変換は、〜N(0,1)、a<1である。
取引可能な平均回帰過程を見つけたのなら、キャベツの入ったカゴを運び出す時間しかない。当然、平均値への回帰率(a)というパラメータにもよるが、どちらにしてもカッコいい。
А вот 1000 случайных блужданий, очевидно виден колокол нормального распределения.
ヒットする周波数を点灯させる必要があります。
--
拡大するダブルキング(ログ)・ベル。
;)
не всякий увидит.
1000個目のサンプルのヒストグラムと確率プロットがありますね。


増分が正規分布であったため、正規分布の和が正規分布となるが。何も確認する必要はありません。
На тебе гистограмму и пробабилити плот для 1000-го отсчёта.
Хотя исходя из того, что приращения были нормальные, сумма нормальных распределений есть нормальное распределение. Тут ничего даже и проверять-то не надо.
センス!
良い(というか-、視覚的に役立つ;)作品ですね。