[アーカイブ!】純粋数学、物理学、化学など:トレードとは一切関係ない脳トレ問題集 - ページ 304 1...297298299300301302303304305306307308309310311...628 新しいコメント Sceptic Philozoff 2010.03.23 20:48 #3031 F(x,y) = min( x, y + 1/x, 1/y ) とすると、以下のようになります。 F(1/y, 1/x) = min( 1/y, 1/x + y, x ) = F(x,y) です。 したがって、yを1/xに、xを1/yに置き換えても、最小値は変わりません。Y=1/xである。 だから、F(x,1/x) = min( x, 2/x, x ) = min( x, 2/x ) となる。x < sqrt(2) ならば x に、そうでなければ 2/x に等しい。 曲線y=xとy=2/xを両方描け。明らかに、最大値はちょうど両者の交点にあり、sqrt(2)に等しい。 問題集に載っている解答は、どちらかというと曖昧で好きではない。 次(8日)です。 この部分はトリビアルに構成されています。陰謀は捨てよう。 問題の第2部(同じく8日)。 理論から実践へ 確率的共振 エンジニア・ガーリンのパラボロイド Sceptic Philozoff 2010.03.23 23:36 #3032 もう一つのフォローは幾何学的(8位)です。 richie 2010.03.24 17:46 #3033 図を簡略化しました。 Sceptic Philozoff 2010.03.24 17:48 #3034 リッチー、どうして陰影のある三角形に等しい角度があるんだ? richie 2010.03.24 17:50 #3035 Mathemat писал(а)>> リッチー、どうして陰影のある三角形に等しい角度があるんだ? 中央のやつで?当たり前のことなんですけどね。 Sceptic Philozoff 2010.03.24 17:53 #3036 続けて証明しなさい。 ところで、問題文には、元の三角形が正三角形であることについては何も書かれていない。正三角形のように描かれていますが。 richie 2010.03.24 17:54 #3037 Mathemat писал(а)>> さあ証明しなさい。 まだ方法がわからないんです。考えておくよ。 - まあ、とにかく、発想はこうでした。 4xの三角形の面積は、大三角形と 4つの小三角形の面積の差の1/3、すなわち4平方cmに等しい。 大三角形の 面積を求めるには、その辺(図中-A)を求める必要があります。 中央の三角形の 辺を面積で求めます。正三角形であることは知っていても問題はなく、 sqr(4*S/sqr(3)) に等しくなります。 михаил потапыч 2010.03.24 17:55 #3038 Richie >>: В центральном? Это очевидно. 中央の三角形を除く3つの三角形が同じである場合のみ しかし、それは条件によると事実ではありません Sceptic Philozoff 2010.03.24 18:02 #3039 それは事実ではありません。 何かしがみつくものがあるはずだ。1つだけ手がかりがあるのですが、まだどうしたらいいのかわかりません。 richie 2010.03.24 18:32 #3040 Mischek писал(а)>> 中央の三角形を除いた3つの三角形が同じである場合のみ。 でも、それは事実ではありません。 そうですか......完全に勘違いしていますね。 大きな三角形は正三角形だと思ってた。小さな3つの三角形は正三角形なので、結果的に似ていることになります。 1...297298299300301302303304305306307308309310311...628 新しいコメント 取引の機会を逃しています。 無料取引アプリ 8千を超えるシグナルをコピー 金融ニュースで金融マーケットを探索 新規登録 ログイン スペースを含まないラテン文字 このメールにパスワードが送信されます エラーが発生しました Googleでログイン WebサイトポリシーおよびMQL5.COM利用規約に同意します。 新規登録 MQL5.com WebサイトへのログインにCookieの使用を許可します。 ログインするには、ブラウザで必要な設定を有効にしてください。 ログイン/パスワードをお忘れですか? Googleでログイン
F(1/y, 1/x) = min( 1/y, 1/x + y, x ) = F(x,y) です。
したがって、yを1/xに、xを1/yに置き換えても、最小値は変わりません。Y=1/xである。
だから、F(x,1/x) = min( x, 2/x, x ) = min( x, 2/x ) となる。x < sqrt(2) ならば x に、そうでなければ 2/x に等しい。
曲線y=xとy=2/xを両方描け。明らかに、最大値はちょうど両者の交点にあり、sqrt(2)に等しい。
問題集に載っている解答は、どちらかというと曖昧で好きではない。
次(8日)です。
この部分はトリビアルに構成されています。陰謀は捨てよう。
問題の第2部(同じく8日)。
図を簡略化しました。
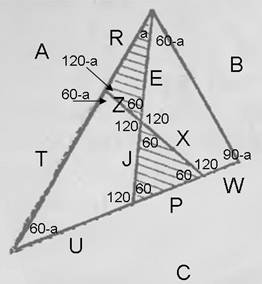
リッチー、どうして陰影のある三角形に等しい角度があるんだ?
ところで、問題文には、元の三角形が正三角形であることについては何も書かれていない。正三角形のように描かれていますが。
さあ証明しなさい。
-
まあ、とにかく、発想はこうでした。
4xの三角形の面積は、大三角形と 4つの小三角形の面積の差の1/3、すなわち4平方cmに等しい。
大三角形の 面積を求めるには、その辺(図中-A)を求める必要があります。
中央の三角形の 辺を面積で求めます。正三角形であることは知っていても問題はなく、 sqr(4*S/sqr(3)) に等しくなります。
В центральном? Это очевидно.
中央の三角形を除く3つの三角形が同じである場合のみしかし、それは条件によると事実ではありません
何かしがみつくものがあるはずだ。1つだけ手がかりがあるのですが、まだどうしたらいいのかわかりません。
中央の三角形を除いた3つの三角形が同じである場合のみ。
でも、それは事実ではありません。
そうですか......完全に勘違いしていますね。
大きな三角形は正三角形だと思ってた。小さな3つの三角形は正三角形なので、結果的に似ていることになります。