不可能を可能にすることは可能か？

[Lilita Bogachkova]

全能感のパラドックス。

パラドックスは通常、"神が自分では持ち上げられない石を作ることができるか？"という問いかけとして定式化される。(そう、創造と解除の無限のサイクルだと思う）あるいは

"神は内角が全部で180度でない三角形を作ることができたか？"（I think Yes, Riemann geometry）。

もし、コロンブスが「ヨーロッパからアメリカまで24時間以内に行くことは可能か」と問われたら、当時の可能性では「不可能」と答えたと思いますが、最近ではどんな子どもでも「可能」と答えるでしょう。 そこで、「その可能性はコロンブスの時代にすでにあったのか、現代になってから現れたのか」という問いを立てます。このことから、「数学と矛盾しないものは、物理的に実現できてもできなくても可能である」と結論づけることができるだろうか。可能性は、私たちが意識しているかどうかにかかわらず、存在するのだ。

[Сергей Криушин]

不可能なことは、神にしか理解できないし、上げることもできない...あるいは反神にしかできない...。

[Maxim Kuznetsov]

パラドックス全般の話題は非常に面白く、徐々に禅につながり、心を開いて考えることを教えてくれる。

1-2+3-4+5シリーズに洗脳されてしまった...=>1/4

愛されないテルワーとマットスタットには、山のようなパラドックスがある :-)

[Alexander Voronkov]

A.アインシュタインが書いています。"気球の表面に住む、完全にペチャンコになった甲虫を想像してください。このカブトムシは分析的な頭脳を持ち、物理学を学び、本も書けるかもしれない。その世界は2次元であろう。頭の中で、あるいは数学的に、3次元が何であるかを理解することはできても、この次元を視覚化することはできないだろう。人間は、このカブトムシとまったく同じ立場にある。ただ、人間は3次元であることが唯一の違いだ。

数学的に4次元を想像することはできても、それを見ること、視覚的に、物理的に想像することはできない。彼にとって、4次元は数学的にしか存在しない。彼の心は四次元を理解できない」（A.アインシュタイン、科学全集第4巻、M.ナウカ、1967年）。

[Dmitry Fedoseev]

Maxim Kuznetsov:

...

愛されないテーバーとマットスタータには、ここに山のようなパラドックスがある :-)

なぜ、ここで急に確率論や数学が 愛されなくなったのでしょうか？こちらでは問題ないようです。しかし、確率論や数学の問題に基づいたナンセンスで。

パラドックスとは何でしょうか？

[Maxim Kuznetsov]

Alexander Voronkov:

A.アインシュタインが書いています。"気球の表面に住む、完全に平らになった虫を想像してください。このカブトムシは分析的な頭脳を持ち、物理学を学び、本も書けるかもしれない。その世界は2次元であろう。頭の中で、あるいは数学的に、3次元が何であるかを理解することはできても、この次元を視覚化することはできないだろう。人間は、このカブトムシとまったく同じ立場にある。ただ、人間は3次元であることが唯一の違いだ。

数学的に4次元を想像することはできても、それを見ること、視覚的に、物理的に想像することはできない。彼にとって、4次元は数学的にしか存在しない。彼の心は四次元を認識することができない」（A.アインシュタイン、全集第4巻、M.ナウカ、1967年）。

アインシュタインとGTR/STO、総じてかっこいいですね。

"0.97℃で巨大なヒキガエルが飛んできました。" "ヒキガエルだとわかりますか？"

[Maxim Kuznetsov]

Dmitry Fedoseev:

なぜここで急に確率論や数学が愛されなくなったのでしょうか？ここでは大丈夫なようです。しかし、確率論や数理統計学に基づくナンセンスには問題がある。

パラドックスとは何でしょうか？

両単位が独立していることを考えると、1+1=2だとさえ思っている。

[romariogold]

[Lilita Bogachkova]

MT4で、テストする時間の降順でEAを自動的にテストすることは可能でしょうか？ 例えば2015.01.01から2015.12.31まで、次のステップは2015.01.02から2015.12.31まで、といった具合にです。

私はオプティマイザーを使ってこの問題を解決しています。

//+------------------------------------------------------------------+
// Внешние переменные 
input bool CheckEvery_Day=false;
input bool TestEachYearSeparately=false;
input int  DayOfYear_=1;
input int  Year_=2009;
// Эксперт функция тик
void OnTick(void)
  {
   if(CheckEvery_Day)
     {
      if(TestEachYearSeparately)
         if(Year()<Year_ || (Year()<=Year_ && DayOfYear()<DayOfYear_) || Year()>Year_) return; //тестировать каждый год отдельно
      else
         if(Year()<Year_ || (Year()<=Year_ && DayOfYear()<DayOfYear_)) return;                 //тестировать весь период 
     }

// Ваш код 

  }
//+------------------------------------------------------------------+

期間を選択します。

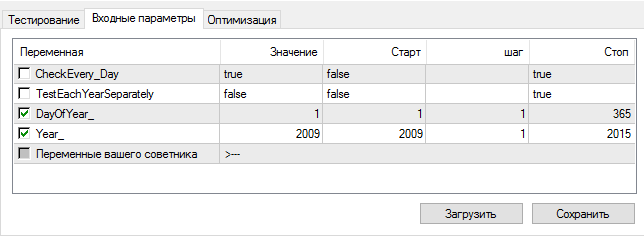
オプティマイザーをオンにします。

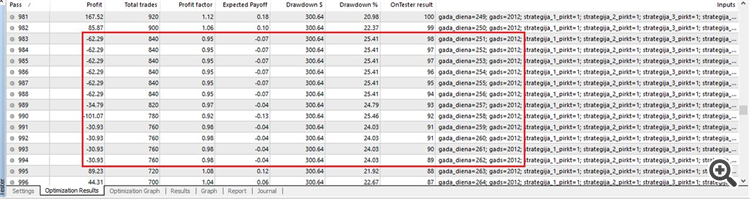
その結果、Expert Advisor が新しい日から開始するたびにテストに合格していることがわかります。

[削除済み]

Dmitry Fedoseev:

なぜここで急に確率論や数学が愛されなくなったのでしょうか？ここでは大丈夫なようです。しかし、確率論や数理統計学に基づくナンセンスには問題がある。

そして、どんなパラドックス？

テレビとMCのパラドックスって初めて聞いた？

ほら、見てください。良い例がたくさんあります。

sekai g / 確率論・数理統計学におけるパラドックス

カテゴリ:数学 2010年3月11日

タイトル：確率論と数理統計学のパラドックス

著者：Seksey G.

概要：ハンガリーの数学者による本書は、確率論、数理統計学、ランダム過程の理論から意外な結論や発言を集めたものである。生き生きと魅力的に書かれており、本書で紹介されている資料は、大学の確率論の講義で説明するために使用でき、いくつかの部分は学校の数学界の仕事でも使用可能である
様々な資格の数学者、確率論や数理統計学を学ぶすべての人向け

pdfでダウンロード (11,4 MB ):Sekey G. / Paradoxes in probability theory and mathematical statistics（確率論と 数理統計学の逆説

vixri．

[Dmitry Fedoseev]

Олег avtomat:

テレビとMSのパラドックスって初めて聞いたか？

チェックしてみてください。良い例がたくさんあります。

Secei G / 確率論と数理統計学におけるパラドックス

カテゴリ:数学 2010年3月11日

タイトル：確率論と数理統計学のパラドックス.

著者：Seckei G.

概要：ハンガリーの数学者による本書は、確率論、数理統計学、ランダム過程論から意外な発見や発言を集めたものである。 活発かつ魅力的に書かれており、大学の確率論の講義で説明用に、また学校の数学サークルの活動で使える部分もある。
様々な資格の数学者、確率論や数理統計学を学ぶすべての人向け

pdfでダウンロード (11,4 MB ):Sekey G. / Paradoxes in probability theory and mathematical statistics（確率論と 数理統計学の逆説

vixri．

そして、何か自身が自分の言葉で書けるようになったのか、リンク上だけで、スクリーンショット上だけなのか。

これから本を読みに行きます。これらのパラドックスのほとんどは、著者の無知、問題の誤った定式化から生じるものである。自分の目と心を開けば、パラドックスはない。