Parmi les indicateurs TA , il existe 5 indicateurs associés aux volumes : A/D (Accumulation Distribution), MFI (Money Flow Index), OBV (On Balance Volume), PVT (Price and Volume Trend ), VROC (Volume Rate of Change). Chacun d'entre eux est censé permettre à un trader de tirer certaines conclusions sur l'évolution des prix. Cependant, à l'exception de l'IMF, tous ces indicateurs n'ont pas de signification claire. C'est-à-dire qu'en fait, leur utilisation ne permet que l'analyse des tendances de ces indicateurs. Et ces modèles, grâce à leurs algorithmes de calcul, répètent en général les mouvements de prix. Mais l'argument "contre" le plus important est le fait que le prix ne peut pas être modifié arbitrairement par un courtier, et que le volume peut être modifié de façon élémentaire. Il suffit de modifier les paramètres de filtrage du tick-flow, que chaque courtier définit indépendamment.
Un autre aspect lié aux volumes est qu'ils dépendent significativement de l'heure de la journée et de la session. Tout le monde le sait, mais cela rend également l'utilisation des volumes via les indicateurs standards assez discutable. Pour compenser cette périodicité, nous devrions au moins comparer les volumes non pas avec les valeurs précédentes, mais avec une norme typique pour l'heure de la journée, le jour de la semaine et la session.
La formulation la plus simple du problème est la suivante.
En forex, il n'y a que 5 jours ouvrables, disons du lundi au vendredi. Bien entendu, pour chaque courtier, en fonction de son fuseau horaire, cet intervalle peut avancer ou reculer. Cependant, comme le forex est un marché mondial, le processus est le même pour tous et sa durée est la même partout.
Supposons que la négociation commence à 00h00 le lundi et se termine à 23h59 le vendredi après la dernière minute de négociation. Cela signifie que nous avons un total de 5x24 = 120 heures par semaine.
Faisons maintenant la somme du volume des transactions de la première heure de tous les lundis et divisons le résultat par leur nombre. Nous obtenons le volume moyen de la première heure du lundi. De même, on obtient le volume moyen de la deuxième heure du lundi, et ainsi de suite, le volume moyen pour chacune des 120 heures de la semaine de travail. La présentation de ces données sous forme de graphique permettra de montrer les changements cycliques des volumes moyens au cours de la semaine. La comparaison de ce graphique avec des graphiques similaires construits pour les années précédentes vous permettra de voir comment cet aspect du marché évolue au fil des ans.
C'était la version la plus simple. Si nous prenons 10 minutes au lieu d'une heure comme intervalle minimum, nous pourrons utiliser un graphique un peu plus intensif, mais tout aussi simple. Cela donnerait 6 fois plus de points dans le tracé, c'est-à-dire 720 points. Et le plus volumineux si l'on prend un intervalle d'une minute. Dans ce cas, il y aura 7200 points. Cette dernière option n'a de sens que si le nombre de ticks par minute est suffisant.
Pour quoi faire ? Le marché est connu pour avoir une structure fractale. A chaque niveau de cette structure peuvent correspondre des effets propres. Pour les détecter, chaque niveau doit être examiné séparément. C'est en fait ce qui a été fait.
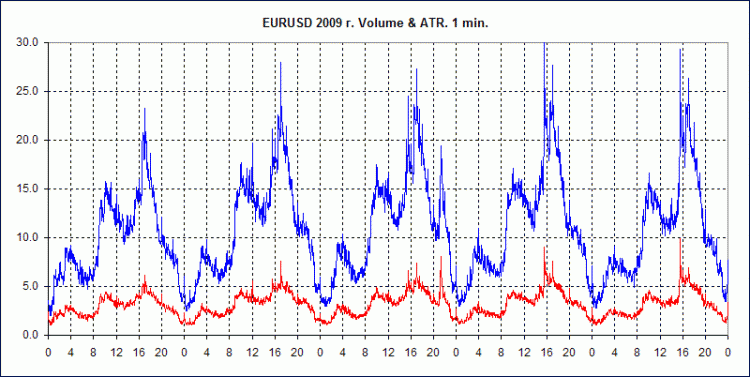
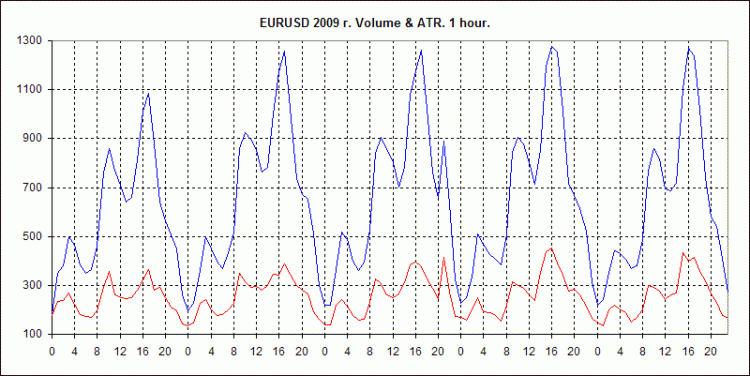
Ci-dessous, 3 graphiques pour EURUSD, 2009. Données de GainCapital.
Ils montrent le comportement des volumes hebdomadaires moyens pour les intervalles H1, M10 et M1, ainsi que les valeurs ATR moyennes calculées de manière similaire pour ces délais.
AvrVOL - volumes moyens, ligne bleue.
AvrATR - valeurs moyennes de l'ATR, ligne rouge.
Sur l'axe des ordonnées - Volume en ticks (pour AvrVOL) et High-Low en points (pour AvrATR).
L'axe des abscisses indique les numéros des heures du jour, de 0 à 23. Le repère est au début de l'heure.
Afin de conserver la visualisation, les valeurs AvrATR sont multipliées par le ratio k=8(pour H1), k=3(pour M10), k=1(pour M1). Autrement dit, pour estimer la valeur réelle de l'AvrATR, vous devez diviser la valeur du graphique par ce coefficient.
Je dois également mentionner que pour H1 et M10 les valeurs AvrVOL sont utilisées directement pour le traçage. Et pour M1, j'ai fait la moyenne des résultats des calculs sur 5 points. Je dois noter tout de suite que ce n'est pas tout à fait la même chose que de calculer les volumes pour le M5. Il permet de réduire un peu l'écart entre les valeurs, mais préserve tous les détails fins du graphique. La formule de calcul de la moyenne est légèrement différente de celle d'un simple SMA. Ici, c'est : AvrVOL[i] = ( AV[i-2] + AV[i-1] + AV[i] + AV[i+1] + AV[i+2] )/5.
Ici AV[i] sont les résultats des calculs du volume moyen pour la i-ème minute de la semaine.
Qu'est-ce qui est intéressant, personnellement, que je vois sur ces graphiques ?
1) Le comportement des volumes est totalement cohérent avec le comportement de l'ATR. Cette correspondance concerne à la fois le comportement des courbes locales et les changements de calendrier. Cependant, le comportement des volumes est plus distinct et leurs valeurs à des TF plus élevées augmentent proportionnellement, ce qui ne peut être dit des valeurs ATR, pour lesquelles cette dépendance à la TF est plus complexe.
2. L'ATR, tout comme le RMS, est utilisé comme mesure de la volatilité du marché. Les graphiques ci-dessus, à mon avis, sont suffisamment convaincants pour conclure que les volumes peuvent également servir de mesure de la volatilité, et qu'ils ne sont pas plus mauvais que les mesures traditionnelles.
Cependant, cette même conclusion rend les volumes impropres à toute évaluation de la direction des prix. La volatilité donne une indication de la nature du mouvement des prix, mais pas de sa direction.
3. une faible volatilité est interprétée comme un caractère de rendement du marché, tandis qu'une volatilité élevée est interprétée comme un caractère de tendance. Une mesure similaire est l'indice Hearst. En ce sens, il sera intéressant de comparer les graphiques ci-dessus avec le graphique correspondant de l'indice Hearst. Mais cela viendra plus tard.
4. Les graphiques montrent clairement la division de chaque journée d'opérations de change en trois vagues - trois sessions : asiatique, européenne et américaine. Pour chacun d'entre eux, le début de la session est associé à une volatilité accrue, qui diminue progressivement jusqu'à la fin. Chaque session est caractérisée par sa propre plage de volatilité. La session asiatique est caractérisée par le minimum, tandis que la session américaine - par le maximum. La volatilité a explosé avant la session américaine lors de la publication des nouvelles, puis une explosion encore plus importante au début de la session est clairement visible. On observe une tendance similaire pour les deux sessions précédentes, mais pas aussi marquée.
5. Un phénomène intéressant est observé lors de la session américaine de mercredi. Quelque part dans la plage des 21-22 heures, on observe à nouveau un pic de volatilité. Il n'y a rien de tel les autres jours ou lors des autres sessions. Pour autant que je sache, à part la déclaration de la FED, qui a lieu 8 fois par an (et la moyenne est en fait de 52 choses), il n'y a pas d'autres événements à ce moment-là. Il est difficile de croire que ces 8 fois ont un tel impact sur le total moyen global. Cependant, pour la volatilité, le communiqué de la FED est probablement l'événement le plus influent. Tout est donc possible.
6. Comme vous pouvez le constater, les 3 graphiques ci-dessus sont très proches les uns des autres. C'est-à-dire qu'il n'y a pas d'effets sur l'un d'entre eux qui manquent sur les autres. D'un côté, ce n'est peut-être pas très beau (on n'a pas trouvé de veines d'or :-), mais d'un autre côté, c'est très optimiste. Cela confirme la fractalité du marché - chaque niveau est semblable aux autres - et permet d'utiliser avec confiance les volumes comme une mesure adéquate de la volatilité, même sur les plus petites TF.
Les volumes ne sont pas souvent utilisés par les traders dans leur TS, pour autant que je sache.
Les indicateurs sont un stratagème marketing - une jolie couverture. Pour ceux qui s'intéressent aux images plutôt qu'aux indicateurs statistiques et aux modèles mathématiques.
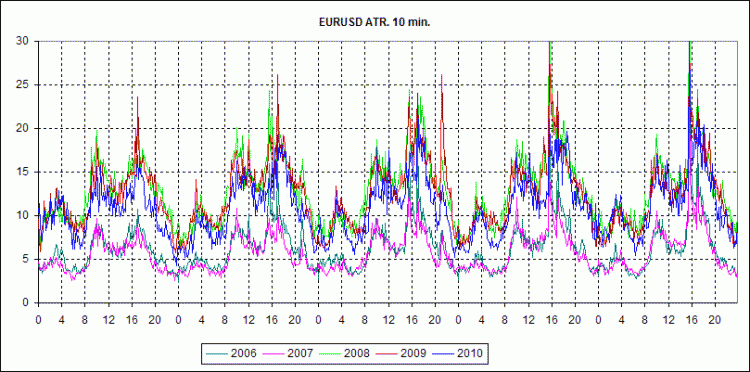
Afin de voir la dynamique des volumes et de l'ATR par année, j'ai réalisé les 2 graphiques ci-dessous.
Ils montrent généralement que la nature du marché a changé en ce sens qu'il est devenu beaucoup plus rapide. À en juger par les pics quotidiens de la session, les volumes ont à peu près doublé. On peut dire la même chose d'ATR. Les courbes des graphiques sont divisées en deux groupes : 2006-2007 et 2008-2009-2010. En effet, la crise qui sévit depuis la mi-2008 a fait tourner la machine à plein régime. Je pense que les courtiers ont simplement dû mettre à niveau le matériel et les logiciels pour rester dans l'air du temps. Et maintenant, il n'y a plus de retour en arrière possible.
Cependant, tout le monde connaît l'augmentation des volumes sans ces graphiques. Mais tous n'ont pas prêté attention au fait que l'ATR a augmenté à peu près dans les mêmes proportions. Et c'est un fait intéressant.
Un autre fait important, à mon avis, est que la nature du caractère cyclique quotidien des marchés n'a pas changé. La crise, et tout ce qui l'a suivi, n'a pas modifié le comportement de la volatilité du marché Forex, ni à l'intérieur des sessions, ni les sessions les unes par rapport aux autres, ni son évolution selon les jours de la semaine. Même le pic de volatilité après 20 heures le mercredi est resté inchangé. Et les petits détails de son comportement n'ont pas d'importance. De toute façon, ils ne faisaient pas partie de ma liste d'objectifs. Ainsi, ce processus aléatoire présente de nombreux aspects stables et cela signifie que la recherche de régularités dans ce processus n'est pas une cause perdue.
La question est de savoir comment l'utiliser. Voici une image simple :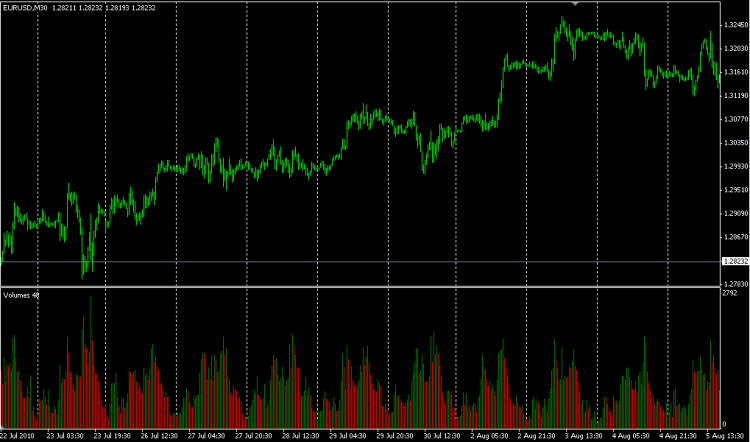
Il est facile de constater qu'en milieu de journée, l'activité commerciale augmente et le prix monte, la nuit, il baisse et ainsi de suite chaque jour, le tableau est à peu près le même. Ce que je veux dire, c'est que si vous regardez le sujet en face, cela n'a aucun sens. Il est judicieux de considérer les volumes réels fournis par de nombreux courtiers comme des valeurs ECN réelles et de voir ce qui se passe. Quant aux ataers et aux trucs comme ça, à mon avis c'est des conneries et c'est inutile.
Revenons maintenant aux volumes et à l'ATR comme mesures de la volatilité. Graphiquement, ils reflètent assez bien son comportement. Il y a cependant un inconvénient. Les deux valeurs ont des dimensions, leurs valeurs moyennes changent au fur et à mesure que les technologies du marché s'améliorent. Cela complique considérablement leur utilisation comme mesure de la volatilité, car l'échelle de ces grandeurs change constamment. Et les utiliser uniquement comme des caractéristiques qualitatives n'est pas intéressant. Ce n'est pas beaucoup mieux que d'utiliser les indicateurs TA standard sur les volumes, que nous avons déjà abandonnés.
La nature similaire de l'évolution des volumes et de l'ATR au fil des ans (les deux pics ont approximativement doublé leur valeur) suggère qu'une mesure quantitative de la volatilité pourrait être le ratio de ces deux valeurs. À ce stade, certains se souviendront certainement de l'indice Hearst. Et à juste titre. :-)
Un mot ou deux sur le rapport Hearst.
En sautant l'historique, mentionnons seulement que la dispersion d'une série aléatoire, selon l'hypothèse de Hearst, est déterminée par le rapport R/S = c * (T)^h. Ici, R est la dispersion d'une série aléatoire, S est sa valeur efficace, T est le temps écoulé depuis le point de départ, c est la constante définie par le processus donné et h est l'exposant de Hurst. Si le RMS d'un processus ne change pas, il peut lui aussi être rangé dans la constante c.
Pour le mouvement brownien, dont les incréments sont décrits par une distribution normale, Einstein a obtenu cette formule de manière explicite. Pour ce cas particulier, h = 1/2. Pour d'autres distributions, h sera évidemment plus ou moins différent de 1/2. Mon opinion personnelle est que la formule de Hurst n'est pas du tout correcte. Je veux dire pour le cas d'une distribution arbitraire. Oui, heureusement pour la distribution normale, elle se plie à une forme si simple. Mais pour le cas arbitraire, cela peut être incommensurablement plus compliqué. Cependant, cette formule est tout à fait adaptée en première approximation (toute fonction T peut être décomposée en série puissance par son argument).
Afin d'appliquer cette formule à notre cas, nous devons déterminer quelques éléments. Tout d'abord, qu'est-ce que T ? À mon avis, l'optimal est le temps intrinsèque ou, comme on dit, le temps opérationnel du marché mesuré en ticks. C'est un compteur, très important - sans dimension, d'événements de processus réels - les changements de prix. Il s'agit donc d'un compteur d'une série de SV. Deuxièmement, quelle est la mesure de la valeur R ? Sa mesure naturelle est le point. Toutefois, cette unité de mesure ne convient pas à toutes les séries. Heureusement, environ 99% des changements de prix dans le flux de données se produisent à 1 point (4 chiffres ! !!). Cela permet de considérer que 1 tick => 1 point (il ne s'agit pas d'un signe "supérieur ou égal à" ). Dans ces conditions, le coefficient de proportionnalité dans la formule de Hurst peut être mis égal à un. Nous avons donc R = (T)^h. A partir de là, il est facile d'obtenir h = Log(R)/Log(T). La base du logarithme n'a pas d'importance.
Ainsi, la forme finale de l'exposant de Hurst est : h = Log(High-Low)/Log(N). Ici, N est le nombre de ticks simples sur l'intervalle de temps, High et Low sont les valeurs de prix maximum et minimum, atteintes sur cet intervalle. Leur différence est exprimée en points à 4 chiffres.
Comme nous pouvons le voir, l'intervalle de temps, pour lequel l'indice de Hurst est déterminé, est toujours présent. Pour les graphiques présentés dans ce sujet, il s'agissait de H1, M10 et M1. Et ce n'est pas un inconvénient, mais un paramètre absolument nécessaire. C'est elle qui détermine à quel niveau fractal se référera l'indice de Hearst calculé.
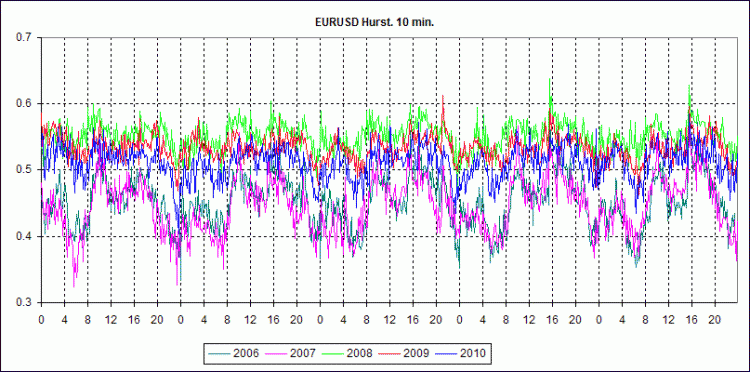
Vous trouverez ci-dessous les graphiques du comportement hebdomadaire de l'indicateur Hearst calculé pour M10 pour 2006-2010.
Comme vous le voyez, son comportement en 2006 et 2007 montre que pendant la majeure partie de la semaine de négociation, le marché de l'euro s'est retourné. En 2008 et, dans une moindre mesure, en 2009, le marché de l'euro a été relativement branché. Cette année, il a oscillé autour du niveau 0,5, ce qui est typique d'une marche aléatoire de Wiener.
Toutefois, il ne s'agit que d'une illustration de ce que vous obtenez lorsque vous utilisez la formule ci-dessus.
À une époque, je me suis beaucoup intéressé à l'algorithme de calcul de l'indice de Hurst. Pour être franc, je n'ai pas aimé plusieurs façons de le calculer trouvées dans la littérature. Cela s'applique également à la méthode décrite par Peters dans son ouvrage Fractal Analysis of Financial Markets, considérée comme fondamentale. Hearst y est défini comme la tangente limite de l'angle de pente du graphique R à T en coordonnées logarithmiques. En conséquence, Hurst est obtenu comme un nombre caractérisant l'ensemble de la série. C'est bien sûr correct, mais peu utile. Je cherchais un algorithme qui permettrait de calculer le Hurst localement, en temps réel. Aujourd'hui, après avoir étudié les statistiques du marché pendant un an, j'ai mis au point un tel algorithme.
Je ne revendique ni l'originalité ni la paternité. Le fait que je ne l'ai pas vu auparavant prouve seulement que je n'ai pas assez regardé.
Je ne sais pas si cet algorithme de calcul de l'indice de Hurst sera utile. Quoi qu'il en soit, cela permet de tirer des conclusions sur la stabilité du marché (ce qui est important pour la stratégie spécifique) et son caractère (ce qui est important pour le choix de cette stratégie), en ayant suivi sa dynamique pendant un long intervalle. Lorsque nous avons déterminé l'indice de Hearst pour l'ensemble de la série en une seule fois (en fait, nous n'avons obtenu que sa moyenne), nous n'avons pas eu une telle opportunité.
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation


Les volumes, pour autant que je sache, ne sont pas souvent utilisés par les traders dans leurs TS. Néanmoins, ils se produisent. C'est pourquoi la question s'est posée de savoir s'ils sont appropriés et, le cas échéant, à quel titre ils peuvent être utilisés. D'autant plus que beaucoup de choses ont changé sur le marché des changes ces dernières années : des signes à 5 chiffres sont apparus, les volumes ont augmenté de manière significative, la crise a commencé, ce qui a également affecté la nature du marché.
Il s'agit d'une préface aux recherches que j'ai effectuées et dont je publie les résultats ici. Je vous préviens tout de suite : il n'y aura pas de grails, pas de TS, pas de recettes toutes faites. Seulement les résultats des études de marché de ces dernières années, qui me permettent de mieux comprendre ce qui se passe et comment certains paramètres peuvent être utilisés. Il n'y aura pas non plus de mathématiques, tout est très simple et illustratif.