Discusión sobre el artículo "Tercera generación de neuroredes: "Neuroredes profundas"" - página 2

Nuevo comentario
 
vlad1949:

No es una pregunta para mí. ¿Eso es todo lo que tienes que decir sobre el artículo?

¿Qué pasa con el artículo? Es una típica reescritura. Es lo mismo en otras fuentes, sólo que con palabras ligeramente diferentes. Incluso las fotos son las mismas. No vi nada nuevo, es decir, de autor.

Quería probar los ejemplos, pero es un fastidio. La sección es para MQL5, pero los ejemplos son para MQL4.

 

vlad1949

Querido Vlad

Mirado a través de los archivos, usted tiene bastante viejo R documentación. Sería bueno cambiar a las copias adjuntas.

Archivos adjuntos:
Doc_R.zip  2181 kb
 

vlad1949

Querido Vlad

¿Por qué no se ejecuta en el probador?

Tengo todo funciona sin problemas. Pero el esquema es sin indicador: el Asesor Experto se comunica directamente con R.

 

Jeffrey Hinton, inventor de las redes profundas: "Las redes profundas sólo son aplicables a datos en los que la relación señal-ruido es grande. Las series financieras son tan ruidosas que las redes profundas no son aplicables. Lo hemos intentado y no ha habido suerte".

Escuche sus conferencias en YouTube.

 
gpwr:

Jeffrey Hinton, inventor de las redes profundas: "Las redes profundas sólo son aplicables a datos en los que la relación señal-ruido es grande. Las series financieras son tan ruidosas que las redes profundas no son aplicables. Lo hemos intentado y no ha habido suerte".

Escucha sus conferencias en youtube.

Teniendo en cuenta su post en el hilo paralelo.

El ruido se entiende de forma diferente en tareas de clasificación que en radioingeniería. Un predictor se considera ruidoso si está débilmente relacionado (tiene débil poder predictivo) para la variable objetivo. Un significado completamente distinto. Hay que buscar predictores que tengan poder predictivo para diferentes clases de la variable objetivo.

 
Yo entiendo el ruido de forma parecida. Las series financieras dependen de un gran número de predictores, la mayoría de los cuales nos son desconocidos y que introducen ese "ruido" en las series. Utilizando únicamente los predictores disponibles públicamente, somos incapaces de predecir la variable objetivo, independientemente de las redes o métodos que utilicemos.
 
gpwr:
Yo entiendo el ruido de forma parecida. Las series financieras dependen de un gran número de predictores, la mayoría de los cuales nos son desconocidos y que introducen ese "ruido" en las series. Utilizando únicamente los predictores disponibles públicamente, somos incapaces de predecir la variable objetivo, independientemente de las redes o métodos que utilicemos.
Véase mi hilo.
 
faa1947:

vlad1949

Querido Vlad

¿Por qué no se ejecuta en el probador?

Tengo todo funciona sin problemas. Cierto el esquema sin indicador: el asesor se comunica directamente con R.

llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll

Buenas tardes SanSanych.

Pues la idea principal es hacer multidivisa con varios indicadores.

De lo contrario, por supuesto, usted puede embalar todo en un Asesor Experto.

Pero si la formación, pruebas y optimización se llevará a cabo sobre la marcha, sin interrumpir el comercio, entonces la variante con un Asesor Experto será un poco más difícil de implementar.

Buena suerte

PS. ¿Cuál es el resultado de las pruebas?

 

Saludos SanSanych.

Aquí tienes algunos ejemplos para determinar el número óptimo de clusters que encontré en algún foro anglosajón. No he podido utilizarlos todos con mis datos. Muy interesante el paquete 11 "clusterSim".

--------------------------------------------------------------------------------------

#
n = 100
g = 6 
set.seed(g)
d <- data.frame(x = unlist(lapply(1:g, function(i) rnorm(n/g, runif(1)*i^2))), 
                y = unlist(lapply(1:g, function(i) rnorm(n/g, runif(1)*i^2))))
plot(d)
--------------------------------------
#1 
library(fpc)
pamk.best <- pamk(d)
cat("number of clusters estimated by optimum average silhouette width:", strpamk.best$nc, "\n")
plot(pam(d, pamk.best$nc))

#2 we could also do:
library(fpc)
asw <- numeric(20)
for (k in 2:20)
  asw[[k]] <- pam(d, k) $ silinfo $ avg.width
k.best <- which.max(asw)
cat("silhouette-optimal number of clusters:", k.best, "\n")
---------------------------------------------------
#3. Calinsky criterion: Another approach to diagnosing how many clusters suit the data. In this case 
# we try 1 to 10 groups.
require(vegan)
fit <- cascadeKM(scale(d, center = TRUE,  scale = TRUE), 1, 10, iter = 1000)
plot(fit, sortg = TRUE, grpmts.plot = TRUE)
calinski.best <- as.numeric(which.max(fit$results[2,]))
cat("Calinski criterion optimal number of clusters:", calinski.best, "\n")
# 5 clusters!
-------------------
4. Determine the optimal model and number of clusters according to the Bayesian Information 
Criterion for expectation-maximization, initialized by hierarchical clustering for parameterized 
Gaussian mixture models
library(mclust)
# Run the function to see how many clusters
# it finds to be optimal, set it to search for
# at least 1 model and up 20.
d_clust <- Mclust(as.matrix(d), G=1:20)
m.best <- dim(d_clust$z)[2]
cat("model-based optimal number of clusters:", m.best, "\n")
# 4 clusters
plot(d_clust)
----------------------------------------------------------------
5. Affinity propagation (AP) clustering, see http://dx.doi.org/10.1126/science.1136800 
library(apcluster)
d.apclus <- apcluster(negDistMat(r=2), d)
cat("affinity propogation optimal number of clusters:", length(d.apclus@clusters), "\n")
# 4
heatmap(d.apclus)
plot(d.apclus, d)
---------------------------------------------------------------------
6. Gap Statistic for Estimating the Number of Clusters. 
See also some code for a nice graphical 
output . Trying 2-10 clusters here:
library(cluster)
clusGap(d, kmeans, 10, B = 100, verbose = interactive())
-----------------------------------------------------------------------
7. You may also find it useful to explore your data with clustergrams to visualize cluster 
assignment, see http://www.r-statistics.com/2010/06/clustergram-visualization-and-diagnostics-for-cluster-analysis-r-code/&nbsp; 
for more details.
-------------------------------------------------------------------
#8. The NbClust package  provides 30 indices to determine the number of clusters in a dataset.
library(NbClust)
nb <- NbClust(d, diss = NULL, distance = "euclidean", 
        min.nc=2, max.nc=15, method = "kmeans", 
        index = "alllong", alphaBeale = 0.1)
hist(nb$Best.nc[1,], breaks = max(na.omit(nb$Best.nc[1,])))
# Looks like 3 is the most frequently determined number of clusters
# and curiously, four clusters is not in the output at all!
-----------------------------------------
Here are a few examples:
d_dist <- dist(as.matrix(d))   # find distance matrix 
plot(hclust(d_dist))           # apply hirarchical clustering and plot
----------------------------------------------------
#9 Bayesian clustering method, good for high-dimension data, more details:
# http://vahid.probstat.ca/paper/2012-bclust.pdf
install.packages("bclust")
library(bclust)
x <- as.matrix(d)
d.bclus <- bclust(x, transformed.par = c(0, -50, log(16), 0, 0, 0))
viplot(imp(d.bclus)$var); 
plot(d.bclus); 
ditplot(d.bclus)
dptplot(d.bclus, scale = 20, horizbar.plot = TRUE,varimp = imp(d.bclus)$var, horizbar.distance = 0, dendrogram.lwd = 2)
-------------------------------------------------------------------------
#10 Also for high-dimension data is the pvclust library which calculates 
#p-values for hierarchical clustering via multiscale bootstrap resampling. Here's #the example from the documentation (wont work on such low dimensional data as in #my example):
library(pvclust)
library(MASS)
data(Boston)
boston.pv <- pvclust(Boston)
plot(boston.pv)
------------------------------------
###Automatically cut the dendrogram
require(dynamicTreeCut)
ct_issues <- cutreeHybrid(hc_issues, inverse_cc_combined, minClusterSize=5)
-----
FANNY <- fanny(as.dist(inverse_cc_combined),, k = 3, maxit = 2000) 
FANNY$membership MDS <- smacofSym(distMat)$conf 
plot(MDS, type = "n") text(MDS, label = rownames(MDS), col = rgb((FANNY$membership)^(1/1)))
-----
m7 <- stepFlexmix
----------------------
#11 "clusterSim" -Department of Econometrics and Computer Science, University of #Economics, Wroclaw, Poland
http://keii.ue.wroc.pl/clusterSim
See file ../doc/clusterSim_details.pdf for further details
data.Normalization Types of variable (column) and object (row) normalization formulas
Description
Types of variable (column) and object (row) normalization formulas
Usage
data.Normalization (x,type="n0",normalization="column")
Arguments
x vector, matrix or dataset
type type of normalization: n0 - without normalization
n1 - standardization ((x-mean)/sd)
n2 - positional standardization ((x-median)/mad)
n3 - unitization ((x-mean)/range)
n3a - positional unitization ((x-median)/range)
n4 - unitization with zero minimum ((x-min)/range)
n5 - normalization in range <-1,1> ((x-mean)/max(abs(x-mean)))
n5a - positional normalization in range <-1,1> ((x-median)/max(abs(x-median)))
n6 - quotient transformation (x/sd)
n6a - positional quotient transformation (x/mad)
n7 - quotient transformation (x/range)
n8 - quotient transformation (x/max)
n9 - quotient transformation (x/mean)
n9a - positional quotient transformation (x/median)
n10 - quotient transformation (x/sum)
n11 - quotient transformation (x/sqrt(SSQ))
normalization "column" - normalization by variable, "row" - normalization by objec
See file ../doc/HINoVMod_details.pdf for further details


En el próximo post cálculos con mis datos

 

El número óptimo de conglomerados puede determinarse mediante varios paquetes y utilizando más de 30 criterios de optimalidad. Según mis observaciones, el criterio más utilizado es el de Calinsky.

Tomemos los datos brutos de nuestro conjunto del indicador dt . Contiene 17 predictores, el objetivo y y el cuerpo de la vela z.

En las últimas versiones de los paquetes "magrittr" y "dplyr " hay muchas nuevas características agradables, una de ellas es 'pipe' - %>%. Es muy conveniente cuando no necesitas guardar resultados intermedios. Preparemos los datos iniciales para el clustering. Tomemos la matriz inicial dt, seleccionemos las últimas 1000 filas de ella, y luego seleccionemos 17 columnas de nuestras variables de ellas. Obtenemos una notación más clara, nada más.

> library(magrittr)
> x<-dt %>% tail( .,1000)%>% extract( ,1:17)

1.

> library(fpc)
> pamk.best <- pamk(x)
> cat("number of clusters estimated by optimum average silhouette width:", pamk.best$nc, "\n")
> number of clusters estimated by optimum average silhouette width: h: 2

2. Criterio de Calinsky: Otro enfoque para diagnosticar cuántos conglomerados se ajustan a los datos. En este caso

probamos de 1 a 10 grupos.

> require(vegan)
> fit <- cascadeKM(scale(x, center = TRUE,  scale = TRUE), 1, 10, iter = 1000)
> plot(fit, sortg = TRUE, grpmts.plot = TRUE)

> calinski.best <- as.numeric(which.max(fit$results[2,]))
> cat("Calinski criterion optimal number of clusters:", calinski.best, "\n")
Calinski criterion optimal number of clusters: 2
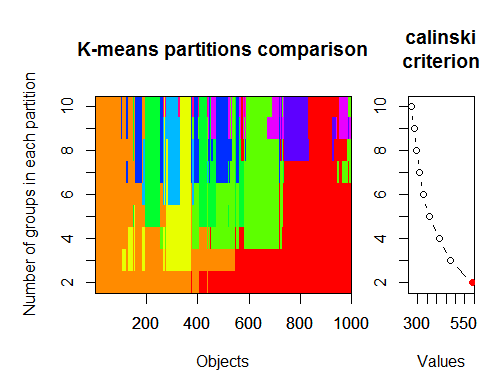
3. Determinar el modelo y el número de grupos óptimos según el criterio de información bayesiano para la maximización de expectativas, inicializado por la agrupación jerárquica para modelos de mezcla gaussiana parametrizados.

Modelos de mezcla gaussiana 

> library(mclust)
#  Run the function to see how many clusters
#  it finds to be optimal, set it to search for
#  at least 1 model and up 20.
> d_clust <- Mclust(as.matrix(x), G=1:20)
> m.best <- dim(d_clust$z)[2]
> cat("model-based optimal number of clusters:", m.best, "\n")
model-based optimal number of clusters: 7
123456789...17
Nuevo comentario