joo
Para empezar, creo que hay que llevar el código a:
1. Compilable.
2. Forma legible.
3. Comentario.
Bien.
Tenemos una matriz ordenada de números reales. Hay que elegir una celda de la matriz con una probabilidad correspondiente al tamaño del sector imaginario de la ruleta.
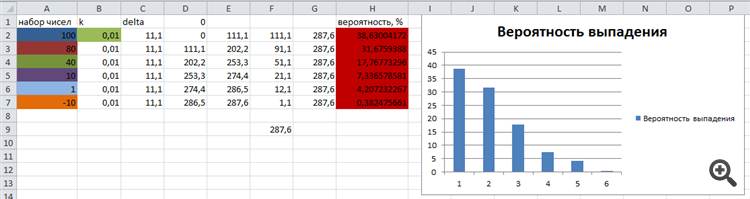
El conjunto de números de prueba y su probabilidad teórica de caer se calculan en Excel y se presentan para su comparación con los resultados del algoritmo en la siguiente imagen:
El resultado de la ejecución del algoritmo:
2012.04.04 21:35:12 Ruleta (EURUSD,H1) h0 38618465 38.618465
2012.04.04 21:35:12 Ruleta (EURUSD,H1) h1 31685360 31.68536
2012.04.04 21:35:12 Ruleta (EURUSD,H1) h3 7.334754 7.334754
2012.04.04 21:35:12 Ruleta (EURUSD,H1) h4 4205492 4.205492
2012.04.04 21:35:12 Ruleta (EURUSD,H1) h5 385095 0.385095
2012.04.04 21:35:12 Ruleta (EURUSD,H1) 12028 ms - Tiempo de ejecución
Como puedes ver, los resultados de la probabilidad de que la "bola" caiga en el sector correspondiente son casi idénticos a los calculados teóricamente.
#property script_show_inputs //--- input parameters input int StartCount=100000000; // Границы соответствующих секторов рулетки double select1[]; // начало сектора double select2[]; // конец сектора //—————————————————————————————————————————————————————————————————————————————— void OnStart() { MathSrand((int)TimeLocal());// сброс генератора // массив с тестовым набором чисел double array[6]={100.0,80.0,40.0,10.0,1.0,-10.0}; ArrayResize(select1,6);ArrayInitialize(select1,0.0); ArrayResize(select2,6);ArrayInitialize(select2,0.0); // счетчики для подсчета выпадений соответствующего числа из тестового набора int h0=0,h1=0,h2=0,h3=0,h4=0,h5=0; // нажмём кнопочку секундомера int time_start=(int)GetTickCount(); // проведём серию испытаний for(int i=0;i<StartCount;i++) { switch(Roulette(array,6)) { case 0: h0++;break; case 1: h1++;break; case 2: h2++;break; case 3: h3++;break; case 4: h4++;break; default: h5++;break; } } Print((int)GetTickCount()-time_start," мс - Время исполнения"); Print("h5 ",h5, " ",h5*100.0/StartCount); Print("h4 ",h4, " ",h4*100.0/StartCount); Print("h3 ",h3, " ",h3*100.0/StartCount); Print("h1 ",h1, " ",h1*100.0/StartCount); Print("h0 ",h0, " ",h0*100.0/StartCount); Print("----------------"); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Рулетка. int Roulette(double &array[], int SizeOfPop) { int i=0,u=0; double p=0.0,start=0.0; double delta=(array[0]-array[SizeOfPop-1])*0.01-array[SizeOfPop-1]; //------------------------------------------------------------------------------ // зададим границы секторов for(i=0;i<SizeOfPop;i++) { select1[i]=start; select2[i]=start+MathAbs(array[i]+delta); start=select2[i]; } // бросим "шарик" p=RNDfromCI(select1[0],select2[SizeOfPop-1]); // посмотрим, на какой сектор упал "шарик" for(u=0;u<SizeOfPop;u++) if((select1[u]<=p && p<select2[u]) || p==select2[u]) break; //------------------------------------------------------------------------------ return(u); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Генератор случайных чисел из заданного интервала. double RNDfromCI(double min,double max) {return(min+((max-min)*MathRand()/32767.0));} //——————————————————————————————————————————————————————————————————————————————
BIEN.
Tenemos una matriz ordenada de números reales. Tenemos que seleccionar una celda de la matriz con una probabilidad correspondiente al tamaño del sector imaginario de la ruleta.
¿Explica el principio de la fijación de la "anchura del sector", que corresponde a los valores de la matriz? ¿O se ajusta por separado?
Esta es la pregunta más oscura, el resto no es un problema.
Segunda pregunta: ¿Qué es el número 0,01? ¿De dónde viene?
En resumen: dime dónde obtener las probabilidades correctas de abandono del sector (anchura como fracción de la circunferencia).
Usted puede sólo el tamaño de cada sector. Siempre (el defecto) que el tamaño negativo no existe en la naturaleza. Incluso en el casino. ;)
¿Explica el principio de la fijación de la "anchura del sector", que corresponde a los valores de la matriz? ¿O se ajusta por separado?
La anchura de los sectores no puede corresponder a los valores de la matriz, de lo contrario el algoritmo no funcionará para todos los números.
Lo que importa es la distancia que hay entre los números. Cuanto más alejados estén todos los números del primero, menos probabilidades habrá de que caigan. En esencia, posponemos en una línea recta barras proporcionales a la distancia entre los números, ajustada por un factor de 0,01, de modo que el último número la probabilidad de caer fuera no era igual a 0 como el más lejano de la primera. Cuanto más alto es el coeficiente, más iguales son los sectores. Se adjunta archivo Excel, experimente con él.
MetaDriver:
1. En resumen: Dígame dónde obtener las probabilidades correctas de abandono del sector (anchura en fracciones de la circunferencia).
2. Puedes simplemente dimensionar cada sector. asumiendo (por defecto) que los tamaños negativos no existen en la naturaleza. ni siquiera en los casinos. ;)1. El cálculo de las probabilidades teóricas se da en excel. El primer número es la mayor probabilidad, el último número es la menor probabilidad, pero no es igual a 0.
2) Los tamaños negativos de los sectores nunca existen para ningún conjunto de números, siempre que el conjunto esté ordenado de forma descendente - el primer número es el mayor (funcionará con el mayor del conjunto pero un número negativo).
La anchura de los sectores no puede coincidir con los valores de la matriz, de lo contrario el algoritmo no funcionará para todos los números.
hu: Lo que importa es la distancia entre los números. Cuanto más separadas estén todas las cifras del primer número, menos probabilidades habrá de que caigan. En esencia, posponemos en una línea recta segmentos proporcionales a las distancias entre los números, ajustados por un factor de 0,01, de modo que la probabilidad de que el último número no caiga fuera 0 como el más alejado del primero. Cuanto más alto es el coeficiente, más iguales son los sectores. Se adjunta el archivo excel, experimenta con él.
1. El cálculo de las probabilidades teóricas se recoge en el excel. El primer número es la mayor probabilidad, el último número es la menor probabilidad, pero no es igual a 0.
2. nunca habrá tamaños negativos de los sectores para cualquier conjunto de números, siempre que el conjunto esté ordenado de forma descendente - el primer número es el mayor (funcionará con el mayor del conjunto pero también con un número negativo).
Su esquema "de la nada" establece la probabilidad del número más pequeño(vmh). No hay ninguna justificación razonable.
// Ya que la "justificación" es un poco difícil. Está bien, sólo hay N-1 espacios entre N clavos.
Así que depende del "coeficiente", también sacado de la caja. ¿Por qué 0,01? ¿Por qué no 0,001?
Antes de hacer el algoritmo, hay que decidir el cálculo de la "anchura" de todos los sectores.
zyu: Da la fórmula para calcular las "distancias entre números". ¿Qué número es el "primero"? ¿A qué distancia se encuentra de sí mismo? No lo envíes a Excel, ya he pasado por eso. Es confuso a nivel ideológico. ¿De dónde viene el factor de corrección y por qué es así?
El que está en rojo no es cierto en absoluto. :)
será muy rápido:
int Selection() { return(RNDfromCI(1,SizeOfPop); }
La calidad del algoritmo en su conjunto no debería verse afectada.
E incluso si lo hace, esta opción superará a la calidad en detrimento de la velocidad.
1. Su esquema "de la nada" establece la probabilidad del número más pequeño(vmh). No hay ninguna justificación razonable. Así que(vmh) depende del "coeficiente" también "fuera de la caja". ¿por qué 0,01 ? ¿por qué no 0,001 ?
2. Antes de hacer el algoritmo, hay que decidir el cálculo de la "anchura" de todos los sectores.
3. zu: Dar la fórmula para calcular las "distancias entre números". ¿Qué número es el "primero"? ¿A qué distancia está de ti? No lo envíes a Excel, ya he pasado por eso. Es confuso a nivel ideológico. ¿De dónde sale el factor de corrección y por qué exactamente?
4. Lo resaltado en rojo no es cierto en absoluto. :)
1. Sí, no es cierto. Me gusta este coeficiente. Si te gusta otro, usaré otro - la velocidad del algoritmo no cambiará.
2. se alcanza la certeza.
3. ok. tenemos un array ordenado de números - array[], donde el número más grande está en array[0], y el rayo de números con un punto de partida 0.0 (puedes tomar cualquier otro punto - nada cambiará) y dirigido en la dirección positiva. Disponga los segmentos en el rayo de esta manera:
start0=0=0 end0=start0+|array[0]+delta|
start1=end0 end1=start1+|array[1]+delta|
start2=end1 end2=start2+|array[2]+delta|
......
start5=end4 end5=start5+|array[5]+delta|
Dónde:
delta=(array[0]-array[5])*0.01-array[5];
Esa es toda la aritmética. :)
Ahora bien, si lanzamos una "bola" sobre nuestro rayo marcado, la probabilidad de golpear un determinado segmento es proporcional a la longitud de ese segmento.
4. Porque has resaltado lo incorrecto (no todo). Deberías destacar:"Esencialmente, estamos trazando en la recta numérica los segmentos proporcionales a las distancias entre los números, corregidos por un factor de 0,01 para que el último número no tenga una probabilidad de llegar a 0".
será muy rápido:
int Selection() { return(RNDfromCI(1,SizeOfPop); }
La calidad del algoritmo en su conjunto no debería verse afectada.
Y si se ve afectada, aunque sea ligeramente, superará la calidad en detrimento de la velocidad.
:)
¿Está sugiriendo que simplemente se seleccione un elemento de la matriz al azar? - Esto no tiene en cuenta las distancias entre los números del array, por lo que su opción es inútil.

- www.mql5.com
:)
¿Está sugiriendo que simplemente se seleccione un elemento de la matriz al azar? - Eso no tiene en cuenta la distancia entre los números de la matriz, por lo que su opción no tiene ningún valor.
no es difícil de comprobar.
¿Está confirmado experimentalmente que no es adecuado?
¿está confirmado experimentalmente que no tiene valor?
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Sugiero que se discutan aquí los problemas de la lógica de los algoritmos óptimos.
Si alguien duda de que su algoritmo tiene una lógica óptima en términos de velocidad (o claridad), entonces es bienvenido.
Además, doy la bienvenida a este hilo a los que quieran practicar sus algoritmos y ayudar a los demás.
Originalmente publiqué mi pregunta en la rama "Preguntas de un Dummie", pero me di cuenta, que no pertenece allí.
Así que, por favor, sugiera una variante del algoritmo de la "ruleta" más rápida que ésta:
Está claro que los arrays se pueden sacar de la función, para no tener que declararlos cada vez y redimensionarlos, pero necesito una solución más revolucionaria. :)