Discusión sobre el artículo "Combinatoria y teoría de la probabilidad en el trading (Parte II): Fractal universal"
Si es posible, pido al autor de este artículo que considere los siguientes argumentos:
Hasta ahora veo que el principio de la proporción áurea se puede utilizar para construir cadenas fractal-probabilísticas que formen un grupo completo de sucesos, pero sinceramente no veo qué puede dar de sí tal enfoque. Parece que la proporción áurea también está conectada con la serie fibo, pero de nuevo no veo cómo se puede aplicar y para qué, si tienes ideas puedes escribir aquí, creo que será un plus aquí. Y así en general estos procesos ya se han formado en mi cabeza, en general eso es todo lo que se necesita para derivar fórmulas más complejas. Hasta ahora los fractales obtenidos cumplen su cometido. Ahí todo va de lo complejo a lo simple y así sucesivamente. Puedo pensar en la aplicación de la proporción áurea, pero no veo cómo será útil. Las series fibo también, todo el mundo dice fibo-fibo ... Ololo, oyen una palabra ingeniosa y la repiten como un loro. Yo siempre parto del hecho de que un principio matemático corresponde a un problema concreto, y siempre encuentro una solución a cualquier problema después de algún tiempo. La herramienta de la solución se selecciona en el proceso, el propio cerebro la encuentra, y si es posible encuentra similitudes con algo que está en el oído. En otras palabras, primero determinamos lo que necesitamos encontrar y luego buscamos la forma de resolver el problema. Me interesaría más escuchar problemas concretos, y puedes hacer un artículo aparte con dichas soluciones, sería interesante y divertido creo yo. En el marco de estos problemas podemos aplicar la proporción áurea y cualquier otra cosa, siempre que el resultado sea realmente necesario y proporcione un beneficio concreto a alguien. Así que puedes escribir sugerencias.
Si es posible, pido al autor de este artículo que considere los siguientes argumentos:
Esto no es más que un mito manido de supuestos fibos y ZS por todas partes....
Lo curioso es que si coges cualquier maceta y la retuerces bien puedes encontrar en ella tanto fibo como proporción áurea y pi y e y muchas otras cosas....
Es sólo un mito trillado de supuestamente fibo y ZS en todas partes y en cualquier lugar ...
Lo curioso es que si coges cualquier maceta y la hilas bien, puedes encontrar en ella el fibo y la proporción áurea y el número de pi y el número de e y muchas otras cosas....
Los fibos (también son la proporción áurea, cosa de la que mucha gente no se da cuenta) se buscan, es decir, se ven, con extrema facilidad. Porque son exponenciales. Que a su vez son sumas...En general, se puede hablar de cosas elementales de la escuela (!!!) durante mucho tiempo, pero es inútil.
También puedes hacerlo así:
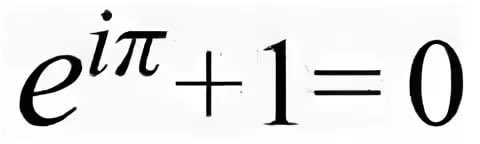
bonito, misterioso...la conexión de FIBO con Fourier...las constantes mundiales en un vaso...y otras cosas.
Es sólo un mito trillado de supuestamente fibo y ZS en todas partes y en cualquier lugar ...
Lo curioso es que si coges cualquier maceta y la hilas bien, puedes encontrar en ella el fibo y la proporción áurea y el número de pi y el número de e y muchas otras cosas....
también puedes encontrar cabeza y hombros en la olla si te la pones en la cabeza).
Es sólo un mito trillado que Fibo y ZS están en todas partes....
Lo curioso es que si coges cualquier maceta y la retuerces bien puedes encontrar en ella fibo y proporción áurea y pi y e y muchas otras cosas....
No podría estar más de acuerdo )) es realmente cierto. A los traders les gusta mucho buscar un significado oculto donde no lo hay ). Yo intento transmitir lo mismo a la gente, pero no sé cómo hacerlo sin decir la verdad, y la verdad es cruel ). He llegado al punto de que hay un problema y hay un conjunto de posibles soluciones, y todo lo que no sea eso es una pérdida de tiempo. Para obtener una solución, primero hay que plantear claramente el problema y tener al menos una idea superficial de las posibles vías de solución del mismo, si no existen tales vías, entonces empieza lo de arriba, Fibonacci, las fórmulas de Euler y demás basura muy bonita pero tan inútil que involuntariamente empiezas a leer entre líneas. Cada herramienta tiene su cometido. A este respecto, propongo ir a lo concreto (tareas concretas).
Hasta ahora veo que el principio de la proporción áurea se puede utilizar para construir cadenas de probabilidad fractal que forman un grupo completo de eventos, pero honestamente no veo lo que este enfoque puede hacer. Parece que la proporción áurea también está conectada con las fiboseries, pero de nuevo no veo cómo se puede aplicar y para qué, si tienes ideas puedes escribir aquí, creo que será un plus aquí. Y así en general estos procesos ya se han formado en mi cabeza, en general eso es todo lo que se necesita para derivar fórmulas más complejas. Hasta ahora los fractales obtenidos cumplen su cometido. Ahí todo va de lo complejo a lo simple y así sucesivamente. Puedo pensar en la aplicación de la proporción áurea, pero no veo cómo será útil. Las series fibo también, todo el mundo dice fibo-fibo ... Ololo, oyen una palabra ingeniosa y la repiten como un loro. Yo siempre parto del hecho de que un principio matemático corresponde a un problema particular, y siempre encuentro una solución a cualquier problema después de algún tiempo. La herramienta de la solución se selecciona en el proceso, el propio cerebro la encuentra, y si es posible encuentra similitudes con algo que está en el oído. En otras palabras, primero determinamos lo que necesitamos encontrar y luego buscamos la forma de resolver el problema. Me interesaría más escuchar problemas concretos, y puedes hacer un artículo aparte con dichas soluciones, sería interesante y divertido creo yo. En el marco de estos problemas podemos aplicar la proporción áurea y cualquier otra cosa, siempre que el resultado sea realmente necesario y proporcione un beneficio concreto a alguien. Así que puedes escribir sugerencias.
1. A lo mejor todo el mundo ha oído hablar de este "ololo", pero yo no escribí sobre el fibo, porque no aconsejo "tirar" de niveles de fibo, aunque si se calculan correctamente, se pueden utilizar, pero en combinación con las ondas de Elliott.
Por supuesto, esto no es todo lo que hay, te das cuenta de lo que consume tiempo y laborioso que es este trabajo, pero empecé este hilo por una razón. Intentaré hacer todo lo que dependa de mí, y en general tales cuestiones, para ser honesto, deberían ser tratadas por todo un equipo de matemáticos y programadores, si no por todo un instituto ¿Qué puede hacer una sola persona contra ello? Aunque tengas un supercerebro, hay tantos datos que procesar que puedes volverte loco. Intento establecer aquellas tareas que se corresponden con mi tiempo y mis capacidades; sí, puedo hacer más, pero ahora no depende de mí. El tiempo es el recurso más valioso. Si hubiera gente interesada en análisis complejos y dedicación completa estaría encantado de hacerlo. No obstante, la rama continuará y cubriré el material que pueda, siempre intento contar algo nuevo, en la medida de mis posibilidades.
El mito sobre la universalidad de la proporción áurea en la naturaleza ha crecido tanto que la gente ni siquiera se molesta en hacer comprobaciones reales, sucumbiendo a los encantos de la belleza de la propia idea de la proporción del todo y sus partes, pero en realidad no es así:
- las conchas de los moluscos-nautilus (que se suelen ilustrar en los artículos sobre la magia de WD) contrariamente a la opinión popular no corresponden a WD.
- proporciones de un cuerpo humano del famoso dibujo de Leonardo Da Vinci "Hombre de Vitruvio" no se observan en relación con personas reales.
- Partenón, Pirámides, otros objetos corresponden muy inexactamente a RS (dibujados por amantes del misticismo).
- Las investigaciones psicológicas objetivas con el fin de revelar si la Inteligencia Emocional es la base de la percepción de la belleza han fracasado con éxito.
- Por último, las pruebas cuantitativas de ruptura/rechazo de niveles en el comercio tampoco muestran que la Inteligencia Emocional sea algo especialmente importante.
La única razón por la que los mercados pueden a veces (palabra clave OTRA vez) hacer un buen pullback/ruptura de los niveles de fibo es por la creencia colectiva de un gran número de operadores técnicos en los niveles de fibo (una profecía autocumplida) si colectivamente ponen sus stops/límites ahí, pero incluso eso probablemente no funcione porque los participantes profesionales, los grandes jugadores institucionales operarán sobre alguna otra base, y la ruptura/inversión del nivel Fibo puede ser simplemente aleatoria, pero para los creyentes en el EQ será sin duda una confirmación de su fe.
Keith Devlin, catedrático de Matemáticas de la Universidad de Stanford, lo explica de forma sencilla: "...... La mayoría de la gente no entiende de matemáticas, y ni siquiera puede entender cómo una fórmula como la proporción áurea se aplica a un sistema complejo, por lo que tampoco puede ponerse a prueba. La gente cree ver la proporción áurea en todas partes, en la naturaleza y en sus objetos favoritos, pero no pueden corroborarlo. Son víctimas de su deseo natural de encontrar un significado a los diversos objetos del universo, pero debido a su falta de conocimientos matemáticos no pueden darse cuenta de que los patrones que detectan son ilusorios."
La gente se programa a sí misma (zombie) para encontrar una explicación sencilla y se esfuerza por mantener esta creencia, ésta es la esencia del pensamiento religioso, incluso en el comercio...
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Artículo publicado Combinatoria y teoría de la probabilidad en el trading (Parte II): Fractal universal:
En el presente artículo, continuaremos estudiando los fractales, prestando especial atención a la generalización de todo el material. En concreto, intentaremos hacer el material más compacto y comprensible, para poder usarlo de forma práctica en el trading.
Comenzaremos tomando las reglas de construcción que obtuvimos en el artículo anterior y completándolas para lograr una comprensión completa de cómo se construye un fractal. Además, hemos localizado un pequeño error en nuestras fórmulas que impedía la asimetría de los límites tanto hacia arriba como hacia abajo. Resulta que hemos obtenido las fórmulas de manera absolutamente correcta, y funcionan para absolutamente cualquier fractal. De hecho, el resultado es una función que permite implementar absolutamente cualquier fractal. Todos los posibles fractales suponen un caso especial de un fractal general. Si tomamos los tres tipos de fractales que hemos definido anteriormente, resultará que las condiciones del fractal general para la implementación de estos tres casos especiales tomarán la forma:
Esquemáticamente, estos tres tipos de fractal tienen el aspecto siguiente:
De forma ideal, obviamente, "S" debería tender al infinito. No hemos descrito las siguientes variables en el artículo anterior, pero las describiremos aquí para obtener una imagen completa sobre el uso de la fórmula general para obtener casos especiales. Un fractal es una función que opera según el principio de reacción en cadena, como en una bomba atómica. Si configuramos una reacción en cadena demasiado profunda, es posible que la computadora no pueda acometer los cálculos; en casos no particularmente críticos, simplemente calculará durante mucho tiempo, a veces minutos, a veces horas, e incluso un día completo.
Autor: Evgeniy Ilin