Diskussion zum Artikel "Neuronale Netzwerke der dritten Generation: Tiefe Netzwerke" - Seite 2

Neuer Kommentar
 
vlad1949:

Das ist keine Frage für mich. Ist das alles, was Sie über den Artikel zu sagen haben?

Was ist mit dem Artikel? Es ist eine typische Umschreibung. Es ist das Gleiche in anderen Quellen, nur in etwas anderen Worten. Sogar die Bilder sind die gleichen. Ich habe nichts Neues, d. h. nichts Autorisches, gefunden.

Ich wollte die Beispiele ausprobieren, aber das ist schade. Der Abschnitt ist für MQL5, aber die Beispiele sind für MQL4.

 

vlad1949

Lieber Vlad!

Ich habe in den Archiven nachgesehen, du hast eine ziemlich alte R-Dokumentation. Es wäre gut, auf die beigefügten Kopien zu wechseln.

Dateien:
Doc_R.zip  2181 kb
 

vlad1949

Lieber Vlad!

Warum hast du im Tester nicht funktioniert?

Ich habe alles funktioniert ohne Probleme. Aber das System ist ohne einen Indikator: der Expert Advisor kommuniziert direkt mit R.

 

Jeffrey Hinton, Erfinder der tiefen Netze: "Tiefe Netze sind nur auf Daten anwendbar, bei denen das Signal-Rausch-Verhältnis groß ist. Finanzreihen sind so verrauscht, dass tiefe Netze nicht anwendbar sind. Wir haben es versucht und hatten kein Glück."

Hören Sie sich seine Vorträge auf YouTube an.

 
gpwr:

Jeffrey Hinton, Erfinder der tiefen Netze: "Tiefe Netze sind nur auf Daten anwendbar, bei denen das Signal-Rausch-Verhältnis groß ist. Finanzreihen sind so verrauscht, dass tiefe Netze nicht anwendbar sind. Wir haben es versucht und hatten kein Glück."

Hören Sie sich seine Vorträge auf youtube an.

In Anbetracht Ihres Beitrags im parallelen Thread.

Rauschen wird bei Klassifizierungsaufgaben anders verstanden als in der Funktechnik. Ein Prädiktor gilt als verrauscht, wenn er nur schwach mit der Zielvariablen zusammenhängt (eine schwache Vorhersagekraft hat). Eine völlig andere Bedeutung. Man sollte nach Prädiktoren suchen, die eine Vorhersagekraft für verschiedene Klassen der Zielvariablen haben.

 
Ich habe ein ähnliches Verständnis von Rauschen. Finanzreihen hängen von einer großen Anzahl von Prädiktoren ab, von denen die meisten uns unbekannt sind und die dieses "Rauschen" in die Reihen einbringen. Wenn wir nur öffentlich verfügbare Prädiktoren verwenden, sind wir nicht in der Lage, die Zielvariable vorherzusagen, egal welche Netze oder Methoden wir verwenden.
 
gpwr:
Ich habe ein ähnliches Verständnis von Rauschen. Finanzreihen hängen von einer großen Anzahl von Prädiktoren ab, von denen die meisten uns unbekannt sind und die dieses "Rauschen" in die Reihen einbringen. Wenn wir nur die öffentlich verfügbaren Prädiktoren verwenden, sind wir nicht in der Lage, die Zielvariable vorherzusagen, egal welche Netze oder Methoden wir verwenden.
Siehe mein Thema.
 
faa1947:

vlad1949

Lieber Vlad!

Warum hast du im Tester nicht funktioniert?

Ich habe alles funktioniert ohne Probleme. Richtig das Schema ohne Indikator: der Advisor kommuniziert direkt mit R.

llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll

Guten Tag SanSanych.

Also die Hauptidee ist es, Multicurrency mit mehreren Indikatoren zu machen.

Ansonsten kann man natürlich alles in einen Expert Advisor packen.

Aber wenn das Training, Testen und Optimieren on the fly erfolgen soll, ohne den Handel zu unterbrechen, dann wird die Variante mit einem Expert Advisor etwas schwieriger zu realisieren sein.

Viel Erfolg!

PS. Was ist das Ergebnis der Tests?

 

Grüße SanSanych.

Hier sind einige Beispiele zur Bestimmung der optimalen Anzahl von Clustern, die ich in einem englischsprachigen Forum gefunden habe. Ich konnte nicht alle davon mit meinen Daten verwenden. Sehr interessant 11 Paket "clusterSim".

--------------------------------------------------------------------------------------

#
n = 100
g = 6 
set.seed(g)
d <- data.frame(x = unlist(lapply(1:g, function(i) rnorm(n/g, runif(1)*i^2))), 
                y = unlist(lapply(1:g, function(i) rnorm(n/g, runif(1)*i^2))))
plot(d)
--------------------------------------
#1 
library(fpc)
pamk.best <- pamk(d)
cat("number of clusters estimated by optimum average silhouette width:", strpamk.best$nc, "\n")
plot(pam(d, pamk.best$nc))

#2 we could also do:
library(fpc)
asw <- numeric(20)
for (k in 2:20)
  asw[[k]] <- pam(d, k) $ silinfo $ avg.width
k.best <- which.max(asw)
cat("silhouette-optimal number of clusters:", k.best, "\n")
---------------------------------------------------
#3. Calinsky criterion: Another approach to diagnosing how many clusters suit the data. In this case 
# we try 1 to 10 groups.
require(vegan)
fit <- cascadeKM(scale(d, center = TRUE,  scale = TRUE), 1, 10, iter = 1000)
plot(fit, sortg = TRUE, grpmts.plot = TRUE)
calinski.best <- as.numeric(which.max(fit$results[2,]))
cat("Calinski criterion optimal number of clusters:", calinski.best, "\n")
# 5 clusters!
-------------------
4. Determine the optimal model and number of clusters according to the Bayesian Information 
Criterion for expectation-maximization, initialized by hierarchical clustering for parameterized 
Gaussian mixture models
library(mclust)
# Run the function to see how many clusters
# it finds to be optimal, set it to search for
# at least 1 model and up 20.
d_clust <- Mclust(as.matrix(d), G=1:20)
m.best <- dim(d_clust$z)[2]
cat("model-based optimal number of clusters:", m.best, "\n")
# 4 clusters
plot(d_clust)
----------------------------------------------------------------
5. Affinity propagation (AP) clustering, see http://dx.doi.org/10.1126/science.1136800 
library(apcluster)
d.apclus <- apcluster(negDistMat(r=2), d)
cat("affinity propogation optimal number of clusters:", length(d.apclus@clusters), "\n")
# 4
heatmap(d.apclus)
plot(d.apclus, d)
---------------------------------------------------------------------
6. Gap Statistic for Estimating the Number of Clusters. 
See also some code for a nice graphical 
output . Trying 2-10 clusters here:
library(cluster)
clusGap(d, kmeans, 10, B = 100, verbose = interactive())
-----------------------------------------------------------------------
7. You may also find it useful to explore your data with clustergrams to visualize cluster 
assignment, see http://www.r-statistics.com/2010/06/clustergram-visualization-and-diagnostics-for-cluster-analysis-r-code/&nbsp; 
for more details.
-------------------------------------------------------------------
#8. The NbClust package  provides 30 indices to determine the number of clusters in a dataset.
library(NbClust)
nb <- NbClust(d, diss = NULL, distance = "euclidean", 
        min.nc=2, max.nc=15, method = "kmeans", 
        index = "alllong", alphaBeale = 0.1)
hist(nb$Best.nc[1,], breaks = max(na.omit(nb$Best.nc[1,])))
# Looks like 3 is the most frequently determined number of clusters
# and curiously, four clusters is not in the output at all!
-----------------------------------------
Here are a few examples:
d_dist <- dist(as.matrix(d))   # find distance matrix 
plot(hclust(d_dist))           # apply hirarchical clustering and plot
----------------------------------------------------
#9 Bayesian clustering method, good for high-dimension data, more details:
# http://vahid.probstat.ca/paper/2012-bclust.pdf
install.packages("bclust")
library(bclust)
x <- as.matrix(d)
d.bclus <- bclust(x, transformed.par = c(0, -50, log(16), 0, 0, 0))
viplot(imp(d.bclus)$var); 
plot(d.bclus); 
ditplot(d.bclus)
dptplot(d.bclus, scale = 20, horizbar.plot = TRUE,varimp = imp(d.bclus)$var, horizbar.distance = 0, dendrogram.lwd = 2)
-------------------------------------------------------------------------
#10 Also for high-dimension data is the pvclust library which calculates 
#p-values for hierarchical clustering via multiscale bootstrap resampling. Here's #the example from the documentation (wont work on such low dimensional data as in #my example):
library(pvclust)
library(MASS)
data(Boston)
boston.pv <- pvclust(Boston)
plot(boston.pv)
------------------------------------
###Automatically cut the dendrogram
require(dynamicTreeCut)
ct_issues <- cutreeHybrid(hc_issues, inverse_cc_combined, minClusterSize=5)
-----
FANNY <- fanny(as.dist(inverse_cc_combined),, k = 3, maxit = 2000) 
FANNY$membership MDS <- smacofSym(distMat)$conf 
plot(MDS, type = "n") text(MDS, label = rownames(MDS), col = rgb((FANNY$membership)^(1/1)))
-----
m7 <- stepFlexmix
----------------------
#11 "clusterSim" -Department of Econometrics and Computer Science, University of #Economics, Wroclaw, Poland
http://keii.ue.wroc.pl/clusterSim
See file ../doc/clusterSim_details.pdf for further details
data.Normalization Types of variable (column) and object (row) normalization formulas
Description
Types of variable (column) and object (row) normalization formulas
Usage
data.Normalization (x,type="n0",normalization="column")
Arguments
x vector, matrix or dataset
type type of normalization: n0 - without normalization
n1 - standardization ((x-mean)/sd)
n2 - positional standardization ((x-median)/mad)
n3 - unitization ((x-mean)/range)
n3a - positional unitization ((x-median)/range)
n4 - unitization with zero minimum ((x-min)/range)
n5 - normalization in range <-1,1> ((x-mean)/max(abs(x-mean)))
n5a - positional normalization in range <-1,1> ((x-median)/max(abs(x-median)))
n6 - quotient transformation (x/sd)
n6a - positional quotient transformation (x/mad)
n7 - quotient transformation (x/range)
n8 - quotient transformation (x/max)
n9 - quotient transformation (x/mean)
n9a - positional quotient transformation (x/median)
n10 - quotient transformation (x/sum)
n11 - quotient transformation (x/sqrt(SSQ))
normalization "column" - normalization by variable, "row" - normalization by objec
See file ../doc/HINoVMod_details.pdf for further details


Im nächsten Beitrag Berechnungen mit meinen Daten

 

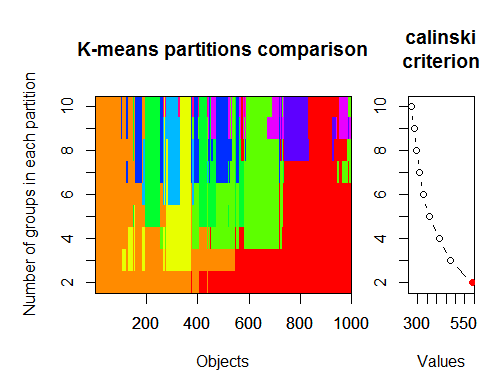
Die optimale Anzahl von Clustern kann mit mehreren Paketen und unter Verwendung von mehr als 30 Optimalitätskriterien bestimmt werden. Nach meinen Beobachtungen istdas am häufigsten verwendete Kriterium das Calinsky-Kriterium.

Nehmen wir die Rohdaten aus unserem Satz des Indikators dt . Er enthält 17 Prädiktoren, das Ziel y und den Candlestick-Körper z.

In den neuesten Versionen der Pakete "magrittr" und "dplyr" gibt es viele neue nette Funktionen, eine davon ist "pipe" - %>%. Sie ist sehr praktisch, wenn Sie Zwischenergebnisse nicht speichern müssen. Bereiten wir die Ausgangsdaten für das Clustering vor. Nehmen Sie die Ausgangsmatrix dt, wählen Sie die letzten 1000 Zeilen aus und wählen Sie dann 17 Spalten unserer Variablen aus. Wir erhalten eine klarere Notation, mehr nicht.

> library(magrittr)
> x<-dt %>% tail( .,1000)%>% extract( ,1:17)

1.

> library(fpc)
> pamk.best <- pamk(x)
> cat("number of clusters estimated by optimum average silhouette width:", pamk.best$nc, "\n")
> number of clusters estimated by optimum average silhouette width: h: 2

2. Calinsky-Kriterium: Ein weiterer Ansatz, um festzustellen, wie viele Cluster zu den Daten passen. In diesem Fall

versuchen wir 1 bis 10 Gruppen.

> require(vegan)
> fit <- cascadeKM(scale(x, center = TRUE,  scale = TRUE), 1, 10, iter = 1000)
> plot(fit, sortg = TRUE, grpmts.plot = TRUE)

> calinski.best <- as.numeric(which.max(fit$results[2,]))
> cat("Calinski criterion optimal number of clusters:", calinski.best, "\n")
Calinski criterion optimal number of clusters: 2
3. das optimale Modell und die Anzahl der Cluster nach dem Bayes'schen Informationskriterium für die Erwartungsmaximierung bestimmen, initialisiert durch hierarchisches Clustering für parametrisierte Gaußsche Mischmodelle.

Gaußsche Mischungsmodelle 

> library(mclust)
#  Run the function to see how many clusters
#  it finds to be optimal, set it to search for
#  at least 1 model and up 20.
> d_clust <- Mclust(as.matrix(x), G=1:20)
> m.best <- dim(d_clust$z)[2]
> cat("model-based optimal number of clusters:", m.best, "\n")
model-based optimal number of clusters: 7
123456789...17
Neuer Kommentar