An den Autor (aus irgendeinem Grund kein Spitzname).
Das gleiche Problem kann auf andere Weise gelöst werden. Es gibt Tests für redundante und fehlende Variablen. Ich könnte das tun und mit Ihren Ergebnissen vergleichen. Aber ich brauche alle Ihre Dateien im .csv-Format.
...ich brauche alle Ihre Dateien im .csv-Format.
Ich glaube, die Quelle befindet sich im Archiv masterdata.zip.
Veröffentlichter Artikel Verwendung der Diskriminanzanalyse zum Aufbau von Handelssystemen:
Autor: ArtemGaleev
Nachdem wir die Variablen ausgewählt haben, müssen wir eine Beziehung zwischen ihnen herstellen, bei der der Preis die abhängige Variable (Funktion) und die anderen Indikatoren die unabhängigen Variablen sind. Hier ist die schematische Gleichung:
Preis Preis(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)
-1 bedeutet den vorherigen Wert. Dies ist normal, da der Indikator analytisch vom Preis abgeleitet wird. Berücksichtigen wir, dass der Preis ein Inkrement ist, so werden wir die Inkremente der Indikatoren nehmen. Aus Faulheit nehme ich nicht alle Indikatoren. Wir schätzen diese Gleichung nach der Methode der kleinsten Quadrate:
Wir haben eine Schätzung der Koeffizienten der Gleichung erhalten. Die letzte Spalte ist sehr interessant: Sie gibt die Wahrscheinlichkeit an, dass der entsprechende Koeffizient gleich Null ist. Diese Wahrscheinlichkeit ist für alle Koeffizienten viel höher als mindestens 10 %, d.h. wir können davon ausgehen, dass wir die Hypothese, dass die entsprechenden Koeffizienten gleich Null sind, nicht zurückweisen können. Dementsprechend hat das R-Quadrat einen lächerlichen Wert.
Daraus schließe ich, dass es sinnlos ist, sich mit der Klassifizierung der Indikatoren zu befassen - sie sind nutzlos, weil sie nichts mit dem Preisanstieg zu tun haben.
Oder liege ich da falsch?
...oder liege ich falsch?
Ich glaube, Sie haben Recht :-)
faa1947, ich habe eine Frage an Sie. Ich wollte ein paar Dinge klären... So habe ich die Daten aus deiner Gleichung berechnet:
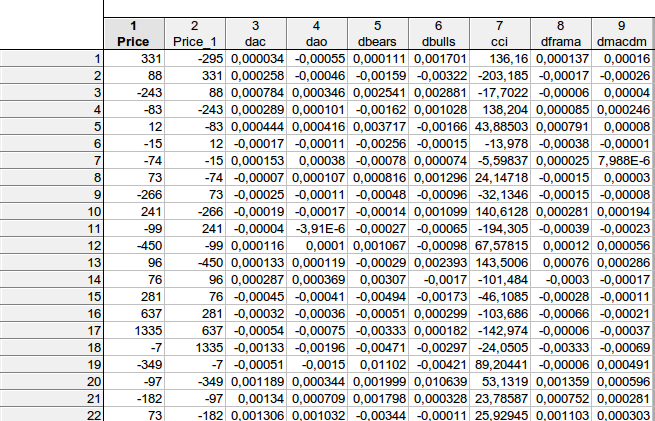
Stimmen die Daten aus der Tabelle mit deiner schematischen Gleichung price price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1) überein?
Und erhielt das folgende Ergebnis:
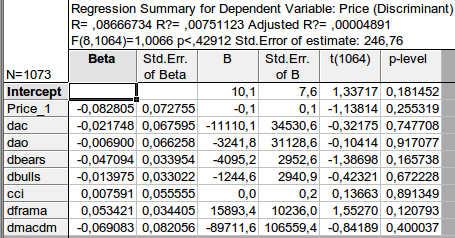
Sobald wir die Variablen ausgewählt haben, müssen wir eine Beziehung zwischen ihnen herstellen, bei der der Preis die abhängige Variable (Funktion) und die anderen Indikatoren die unabhängigen Variablen sind. Hier ist eine schematische Gleichung:
Preis Preis(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)
-1 bedeutet den vorherigen Wert. Dies ist normal, da der Indikator analytisch vom Preis abgeleitet wird. Berücksichtigen wir, dass der Preis ein Inkrement ist, so werden wir die Inkremente der Indikatoren nehmen. Aus Faulheit nehme ich nicht alle Indikatoren. Schätzen wir diese Gleichung mit der Methode der kleinsten Quadrate:
Wir haben eine Schätzung der Koeffizienten der Gleichung erhalten. Die letzte Spalte ist sehr interessant: Sie gibt die Wahrscheinlichkeit an, dass der entsprechende Koeffizient gleich Null ist. Diese Wahrscheinlichkeit ist für alle Koeffizienten viel höher als mindestens 10 %, d.h. wir können davon ausgehen, dass wir die Hypothese, dass die entsprechenden Koeffizienten gleich Null sind, nicht zurückweisen können. Dementsprechend hat das R-Quadrat einen lächerlichen Wert.
Daraus schließe ich, dass es sinnlos ist, sich mit der Klassifizierung der Indikatoren zu befassen - sie sind nutzlos, weil sie nichts mit dem Preisanstieg zu tun haben.
Oder liege ich da falsch?
Nennen Sie bitte die von Ihnen verwendete statistische Methode. Es war die Konstruktion einer linearen Regressionsgleichung, bei der der Input die Indikatoren und der Output der zukünftige Preis ist? Ist das richtig? Diese Methode ist für Devisen nicht geeignet, da es sich nicht um ein lineares, deterministisches System handelt. Die Diskriminanzanalyse hat eine andere Aufgabe, sie erstellt Modelle zur Mustererkennung auf der Grundlage externer Beschreibungen des Systems.
Wenn die Klassifizierung von Indikatoren zur Analyse von Kurssteigerungen nutzlos wäre, dann wäre die technische Analyse sinnlos. Glücklicherweise verhält sich der Kurs nicht chaotisch, er hat ein Gedächtnis für frühere Ereignisse.
Sie scheinen Recht zu haben :-)
faa1947, ich habe eine Frage an Sie. Ich wollte ein paar Dinge klären... So habe ich die Daten aus Ihrer Gleichung berechnet:
Stimmen die Daten aus der Tabelle mit deiner schematischen Gleichung price price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1) überein?
Und erhielt das folgende Ergebnis:
Die Rohdaten sehen wie folgt aus:
Die Gleichungen sehen wie folgt aus:
Schätzung Gleichung:
=========================
PRICE = C(1)*PRICE(-1) + C(2)*DAC(-1) + C(3)*DAO(-1) + C(4)*DBEARS(-1) + C(5)*DBULLS(-1) + C(6)*CCI(-1) + C(7)*DFRAMA(-1) + C(8)*DMACDM(-1)
Substituierte Koeffizienten:
=========================
PREIS = -0.0228102658125*PREIS(-1) + 12005.8974278*DAC(-1) + 4033.10946937*DAO(-1) + 3176.11232129*DBEARS(-1) - 6021.36196728*DBULLS(-1) - 0.102710105369*CCI(-1) - 11487.4273249*DFRAMA(-1) + 62535.3387412*DMACDM(-1)
Ich verstehe Ihre Berechnung nicht. Ich habe das Prinzip der Verwendung des Lag-Wertes (früherer Wert). Dadurch ist es möglich, eine Vorhersage zu treffen. Wenn Lag -1 der ersten Beobachtung entspricht, dann entspricht die abhängige Variable einer neuen, vorhergesagten, unbeobachteten Beobachtung.
Was ist der p-Wert? Für mich ist es die Wahrscheinlichkeit, dass der entsprechende Koeffizient Null ist.
Bitte geben Sie die Bezeichnung der von Ihnen verwendeten statistischen Methode an. Handelt es sich um eine lineare Regressionsgleichung, bei der der Input die Indikatoren und der Output der zukünftige Preis ist? Ist das korrekt?
Die Regression wurde nach der Methode der kleinsten Quadrate geschätzt. Sie kann für Vorhersagen verwendet werden.
Bei Devisen funktioniert dies nicht, da es sich nicht um ein lineares deterministisches System handelt.
Wenn es linear ist, dann nur in einem bestimmten Beispiel. Es ist nicht deterministisch, weil sogar die Koeffizienten als Zufallsvariablen behandelt werden. Alle Koeffizienten werden nicht berechnet, sondern geschätzt. In der zweiten Spalte ist der Standardfehler der Koeffizientenschätzung angegeben. Bitte beachten Sie, dass er sehr groß ist.
Wäre die Klassifizierung der Indikatoren für die Analyse von Kurssteigerungen unbrauchbar, wäre die technische Analyse sinnlos.
Genau so ist es, und ich wage Ihnen zu versichern, dass ich nicht der einzige bin, der so denkt. Die TA ist keine Wissenschaft, sondern eine Art Astrologie. Ursprünglich, vor 300 Jahren, war sie ein System zur Visualisierung des Kotirs. Seitdem hat sie sich enorm weiterentwickelt. Alles andere ist für die Pinocchios auf dem Gebiet der Wunder. Ich habe mich über Ihren Artikel gefreut, da er einige regelmäßige und wiederholbare Gedanken enthält.
Wenn die Klassifizierung der Indikatoren für die Analyse des Kursanstiegs nutzlos war
Wir habenhier einen Spezialfall von Indikatoren analysiert. Es ist immer notwendig zu beweisen, dass ein bestimmter Indikator oder seine Verwendung etwas mit einem Kurs zu tun hat. Die TA berücksichtigt diese Frage nie.
Glücklicherweise verhält sich der Kurs nicht chaotisch, er hat ein Gedächtnis für frühere Ereignisse.
Die gesamte Ökonometrie beruht auf der Annahme, dass ein Kurs eine deterministische Komponente (Autokorrelation, Gedächtnis) und Rauschen hat.
Die Diskriminanzanalyse hat eine andere Aufgabe: Sie erstellt Modelle zur Mustererkennung auf der Grundlage externer Beschreibungen des Systems.
Die Aufgabe ist klar. Die Frage ist jedoch, ob man dem erzielten Ergebnis trauen kann. Das Problem ist nicht die Klassifizierung (das ist ein Teil des Problems, das auch gelöst werden muss), sondern das Vertrauen in die resultierende Vorhersage. Und genau das ist das Problem.
Ich verstehe Ihre Berechnung nicht. Mein Prinzip ist es, den Verzögerungswert (früherer Wert) zu verwenden. Dies ermöglicht es, eine Vorhersage zu treffen. Wenn Lag -1 der ersten Beobachtung entspricht, dann entspricht die abhängige Variable einer neuen, vorhergesagten, unbeobachteten Beobachtung.
Was ist der p-Wert? Für mich ist es die Wahrscheinlichkeit, dass der entsprechende Koeffizient Null ist.
faa1947, ich habe die Tabelle mit den Verzögerungen angegeben (für die ersten paar Zeilen - ich kann nicht die ganze Tabelle anpassen). Aber zuerst habe ich die Indikatordifferenzen berechnet, so dass die Gesamtzahl der Zeilen 1073 statt 1074 beträgt. Dann habe ich die abhängige Variable Preis einen Schritt nach vorne verschoben.
Es stellte sich heraus, dass für das Beispiel der 1:
331 = C(1)*(-295) + C(2)* 0.000034+ C(3)* (-0.00055) + C(4)* 0.000111 + C(5)* 0.001701+ C(6)*136.16+ C(7)* 0.000137+ C(8)*0.00016, sofern
PREIS = C(1)*PREIS(-1) + C(2)*DAC(-1) + C(3)*DAO(-1) + C(4)*DBEARS(-1) + C(5)*DBULLS(-1) + C(6)*CCI(-1) + C(7)*DFRAMA(-1) + C(8)*DMACDM(-1)
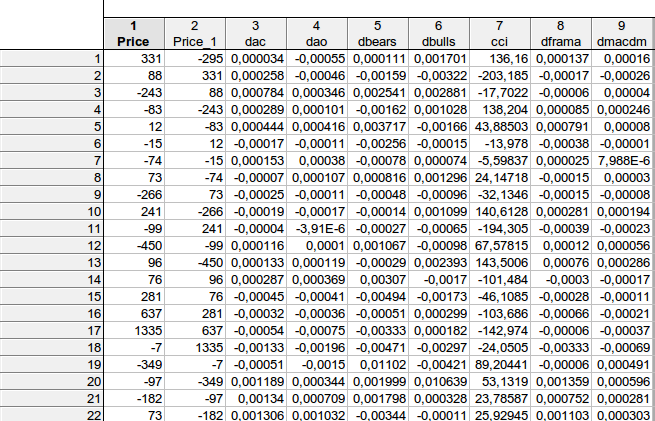
Im Allgemeinen habe ich ungefähr ein ähnliches Ergebnis erhalten - es gibt keine Möglichkeit, die Nullhypothese, dass die betrachteten Koeffizienten gleich Null sind, zurückzuweisen...
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Neuer Artikel Erstellung von Handelssystemen mittels Diskriminanzanalyse :
Bei der Erstellung von Handelssystemen stellt sich für gewöhnlich die Frage nach der Auswahl der besten Kombination von Indikatoren und deren Signalen. Die Diskriminanzanalyse (DA) ist eines der Verfahren zur Ermittlung dieser Kombinationen. In diesem Beitrag werden ein Beispiel für die Entwicklung eines Expert-Systems zur Erfassung von Marktdaten vorgestellt und der Einsatz der DA zur Erstellung von Vorhersagemodellen für den Devisenmarkt in einem Programm von Statistica vorgeführt.
Zum Herunterladen der Datei nach Statistica gehen wir wie folgt vor:
Abbildung 1. Import der Datei nach Statistica
Nach Anklicken von OK erhalten wir die Tabelle mit unseren Daten.
Abbildung 2. Datenbank in Statistica
Autor: ArtemGaleev