Linearer Regressionskanal

Dmitiry Ananiev 2019.07.27 15:39

Ich habe einen Indikator für eine lineare Regression.

Wie die Berechnung in EA zu bauen und Daten auf 0 bar oder auf 1 erhalten.

Ich habe versucht, es so zu machen:

enum ENUM_Polynomial
  {
   linear=1,      // linear 
   parabolic=2,   // parabolic 
   Third_power=3, // third-power 
  };
input ENUM_Polynomial degree=linear;
input double kstd=2.0;
input int bars=250;
input int shift=0;

double Ask,Bid;
double h,l;
double sqh_buffer[];
double fx_buffer[];
double sql_buffer[];
double close[];

double ai[10,10],b[10],x[10],sx[20];
double sum;
int p,n,f;
double qq,mm,tt;
int ii,jj,kk,ll,nn;
double sq;

int i0=0;
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
int OnInit()
  {
   
   ArrayResize(fx_buffer,1000);
   ArrayResize(sqh_buffer,1000);
   ArrayResize(sql_buffer,1000);
   
   ArraySetAsSeries(fx_buffer,true);
   ArraySetAsSeries(sqh_buffer,true);
   ArraySetAsSeries(sql_buffer,true);
   
   ArrayResize(close,1000);
   ArraySetAsSeries(close,false);
   
   
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {

  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void OnTick()
  {
   MqlTick Tick;
   SymbolInfoTick(_Symbol,Tick);

   Ask = Tick.ask;
   Bid = Tick.bid;
   
   
   iStdev
   for (int i =0; i<1000;i++)
   {
     // Print (i, "   ",ArraySize(close)); 
    close[i] = iClose(_Symbol,0,0);
   }
   
  // ArraySetAsSeries(close,true);
   int mi;
   p=bars;
   sx[1]=p+1;
   nn=degree+1;
   
   //--- sx 
   for(mi=1;mi<=nn*2-2;mi++)
     {
      sum=0;
      for(n=i0;n<=i0+p;n++)
        {
         sum+=MathPow(n,mi);
        }
      sx[mi+1]=sum;
     }
//--- syx 
   for(mi=1;mi<=nn;mi++)
     {
      sum=0.00000;
      for(n=i0;n<=i0+p;n++)
        {
         if(mi==1)
            sum+=close[n];
         else
            sum+=close[n]*MathPow(n,mi-1);
        }
      b[mi]=sum;
     }
//--- Matrix 
   for(jj=1;jj<=nn;jj++)
     {
      for(ii=1; ii<=nn; ii++)
        {
         kk=ii+jj-1;
         ai[ii,jj]=sx[kk];
        }
     }
//--- Gauss 
   for(kk=1; kk<=nn-1; kk++)
     {
      ll=0;
      mm=0;
      for(ii=kk; ii<=nn; ii++)
        {
         if(MathAbs(ai[ii,kk])>mm)
           {
            mm=MathAbs(ai[ii,kk]);
            ll=ii;
           }
        }
     
      if(ll!=kk)
        {
         for(jj=1; jj<=nn; jj++)
           {
            tt=ai[kk,jj];
            ai[kk,jj]=ai[ll,jj];
            ai[ll,jj]=tt;
           }
         tt=b[kk];
         b[kk]=b[ll];
         b[ll]=tt;
        }
      for(ii=kk+1;ii<=nn;ii++)
        {
         qq=ai[ii,kk]/ai[kk,kk];
         for(jj=1;jj<=nn;jj++)
           {
            if(jj==kk)
               ai[ii,jj]=0;
            else
               ai[ii,jj]=ai[ii,jj]-qq*ai[kk,jj];
           }
         b[ii]=b[ii]-qq*b[kk];
        }
     }
   x[nn]=b[nn]/ai[nn,nn];
   for(ii=nn-1;ii>=1;ii--)
     {
      tt=0;
      for(jj=1;jj<=nn-ii;jj++)
        {
         tt=tt+ai[ii,ii+jj]*x[ii+jj];
         x[ii]=(1/ai[ii,ii])*(b[ii]-tt);
        }
     }
//---
   for(n=i0;n<=i0+p;n++)
     {
      sum=0;
      for(kk=1;kk<=degree;kk++)
        {
         sum+=x[kk+1]*MathPow(n,kk);
        }
      fx_buffer[n]=x[1]+sum;
     }
//--- Std 
   sq=0.0;
   for(n=i0;n<=i0+p;n++)
     {
      sq+=MathPow(close[n]-fx_buffer[n],2);
     }
   sq=MathSqrt(sq/(p+1))*kstd;

   for(n=i0;n<=i0+p;n++)
     {
      sqh_buffer[n]=fx_buffer[n]+sq;
      sql_buffer[n]=fx_buffer[n]-sq;
     }
     
     h = sqh_buffer[
0];
     l = sql_buffer[0];

Aber es gibt nichts her...

Dateien:

i-Regr.mq5 12 kb

Maxim Dmitrievsky 2019.07.27 16:00 #1

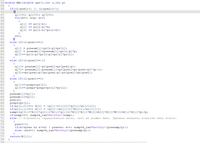
void calcPolynomialRegression(double &PricesArray[],double &RegressionArray[], int power) {
 ArrayResize(RegressionArray, ArraySize(PricesArray)); ArraySetAsSeries(RegressionArray,ArrayGetAsSeries(PricesArray));
 double summ_x_value[21],summ_y_value[11],constant[11],matrix[11][11];
 ArrayInitialize(summ_x_value,0); ArrayInitialize(summ_y_value,0);
 ArrayInitialize(constant,0); ArrayInitialize(matrix,0);

 double summ=0,summ_x=0,summ_y=0;
 int pos=ArraySize(PricesArray)-1;
 summ_x_value[0]=ArraySize(PricesArray);
 for(int exp_n=1; exp_n<=2*power; exp_n++) {
  summ_x=0;
  summ_y=0;
  for(int k=1; k<=ArraySize(PricesArray); k++) {
   summ_x+=MathPow(k,exp_n);
   if(exp_n==1) summ_y+=PricesArray[pos-k+1];
   else if(exp_n<=power+1) summ_y+=PricesArray[pos-k+1]*MathPow(k,exp_n-1); }
  summ_x_value[exp_n]=summ_x;
  if(summ_y!=0) summ_y_value[exp_n-1]=summ_y; }

 for(int row=0; row<=power; row++)
  for(int col=0; col<=power; col++)
    matrix[row][col]=summ_x_value[row+col];

 int initial_row=1;
 int initial_col=1;
 for(int i=1; i<=power; i++) {
  for(int row=initial_row; row<=power; row++) {
   summ_y_value[row]=summ_y_value[row]-(matrix[row][i-1]/matrix[i-1][i-1])*summ_y_value[i-1];
   for(int col=initial_col; col<=power; col++)
     matrix[row][col]=matrix[row][col]-(matrix[row][i-1]/matrix[i-1][i-1])*matrix[i-1][col]; }
   initial_col++;
   initial_row++; }
   
 int j=0;
 for(int i=power; i>=0; i--) {
  if(j==0) constant[i]=summ_y_value[i]/matrix[i][i];
  else {
   summ=0;
   for(int k=j; k>=1; k--) summ+=constant[i+k]*matrix[i][i+k];
   constant[i]=(summ_y_value[i]-summ)/matrix[i][i]; }
  j++; }
  
 int k=1;
 for(int i=ArraySize(PricesArray)-1; i>=0; i--) {
  summ=0;
  for(int n=0; n<=power; n++) summ+=constant[n]*MathPow(k,n);
  RegressionArray[i]=summ;
  k++; } }

Georgiy Merts 2019.07.27 17:02 #2

Auch wenn Sie kein OOP verwenden - ich würde den Code in eine Reihe von Funktionen aufteilen, um ihn sinnvoll zu gestalten.

Nikolai Semko 2019.07.27 17:23 #3

Ich habe eine Regressionsberechnung (nicht nur linear) ganz ohne Zyklen implementiert. Genauer gesagt, wird ein Zyklus nur einmal während der Initialisierung benötigt.
Das Ergebnis ist eine tausendfach höhere Rechengeschwindigkeit.

Und der Code ist kürzer.
Aber es tut mir leid, ich werde den Code nicht veröffentlichen. Das ist ein Geheimnis.
Ich sage nur, dass es real ist.

Fehler, Irrtümer, Fragen Paarhandel und Arbitrage in Wer handelt mit dem

Rashid Umarov 2019.07.27 19:04 #4

Zwei Artikel sind hilfreich

Пример разработки спредовой стратегии на фьючерсах Московской биржи

www.mql5.com

MetaTrader 5 позволяет разрабатывать и тестировать роботов, торгующих одновременно на нескольких инструментах. Встроенный в платформу тестер стратегий автоматически скачивает с торгового сервера брокера тиковую историю и учитывает спецификацию контрактов — разработчику ничего не нужно делать руками. Это позволяет легко и максимально...

Yuriy Asaulenko 2019.07.27 19:06 #5

Nikolai Semko:

Ich habe die Berechnung der Regression (nicht nur linear) ganz ohne Zyklen implementiert. Um genauer zu sein, wird die Schleife nur einmal bei der Initialisierung benötigt.
Das Ergebnis ist eine tausendfach höhere Rechengeschwindigkeit.

Und der Code ist kürzer.
Aber es tut mir leid, ich werde den Code nicht veröffentlichen. Das ist ein Geheimnis.
Ich sage nur, dass es real ist.

Der Code ist sehr einfach. Wir addieren die aktuellen Quadrate und subtrahieren die Quadrate außerhalb des Intervalls. Das war's. Das ist das ganze Geheimnis.)

Es kann sogar noch interessanter sein, aber nach anderen Prinzipien.

Helfen Sie mir, ein Paarhandel und Arbitrage in Machen Sie Ihre erste

Nikolai Semko 2019.07.27 20:06 #6

Yuriy Asaulenko:

Der Code ist sehr einfach. Wir addieren die aktuellen Quadrate und subtrahieren die Quadrate außerhalb des Intervalls. Das war's. Das ist das Geheimnis.)

lustig )))

Yuriy Asaulenko 2019.07.27 20:18 #7

Nikolai Semko:
lustig ))

Um es noch lustiger zu machen, könnten Sie nicht über den Kanal berichten, sondern darüber, wie man eine polynomiale Regressionslinie ohne Zyklen erstellt. Aber das werde ich definitiv nicht tun. Sie brauchen es nicht.

[Archiv!] Jede Anfängerfrage, um Interessant und humorvoll FOREX - Trends, Prognosen

Georgiy Merts 2019.07.28 04:24 #8

Nikolai Semko:

Ich habe eine Regressionsberechnung (nicht nur linear) ganz ohne Zyklen durchgeführt. Genauer gesagt, wird der Zyklus nur einmal während der Initialisierung benötigt.
Dadurch wird die Berechnungsgeschwindigkeit um das Tausendfache erhöht.

Und der Code ist kürzer.
Aber es tut mir leid, ich werde den Code nicht veröffentlichen. Das ist ein Geheimnis.
Ich sage nur, dass es real ist.

Tausendmal schneller und ohne eine Schleife von Eingabewerten...

Ich kann es nicht glauben!!!

Zumindest eine Schleife der Eingabeparameter ist obligatorisch!

Dmitry Fedoseev 2019.07.28 04:44 #9

Nikolai Semko:

Ich habe eine Regressionsberechnung (nicht nur linear) ganz ohne Zyklen implementiert. Genauer gesagt, wird die Schleife nur einmal bei der Initialisierung benötigt.
Das Ergebnis ist eine tausendfach höhere Rechengeschwindigkeit.

Und der Code ist kürzer.
Aber es tut mir leid, ich werde den Code nicht veröffentlichen. Das ist ein Geheimnis.
Ich sage nur, dass es real ist.

Und auch ohne eine x*y-Summenschleife? Und wenn x und y keine Geraden sind?

Nikolai Semko 2019.07.28 07:36 #10

Georgiy Merts:

Tausendmal schneller und ohne eine Schleife von Eingabewerten...

Ich kann es nicht glauben!!!

Zumindest eine Schleife über die Eingabeparameter ist obligatorisch!

Dmitry Fedoseev:

Und auch ohne eine x*y-Summenschleife ? Was ist, wenn x und y keine Geraden sind?

Glauben Sie es nicht für bare Münze.
Rashid ließ die Artikel fallen. Lesen Sie sie sorgfältig. Dort gibt es einen Link zu einem anderen Artikel:
https://www.mql5.com/ru/articles/270

Wenn Sie sich auf dem Niveau der 7. bis 8. Klasse das Hirn zermartern, können Sie die Standardabweichung ermitteln, um den Kanal, nicht nur den gleitenden Durchschnitt, auf ähnliche Weise ohne einen Zyklus zu erhalten. Ich habe dies für ein Polynom beliebigen Grades implementiert, nicht nur für den ersten Grad (lineare Regression). Sie können es in der Demoversion auf dem Marktplatz erleben.

HH Ich habe geschrieben, dass die Schleife einmal bei der Initialisierung benötigt wird.

Tausendmal schneller - auch bei der Berechnung der Standardabweichung (d.h. der Kanalbreite)

Hilf mir, die Ordnung Helfen Sie jedem, den Jede Anfängerfrage, um das

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

Neuer Kommentar