Nun, wie wäre es, wenn wir (nur nach Augenmaß) sagen, dass es sich um einen Sinus handelt, mit einer stetig zunehmenden Periode (abhängig von X), d.h. eine Formel wie diese:
Allgemeines (woher wir kommen):
Y=sin( K*X+T)
Wir sagen nun, dass der Parameter K auch von X abhängt. Die ganze Zeit über steigt oder sinkt sie. Es stellt sich die Frage: Ist sie linear? Ich würde davon ausgehen, dass sie zunächst linear verläuft. Dann ist es A*X+B (Linienformel). Eingesetzt in die ursprüngliche Formel erhalten wir
Y=sin((A*X+B)*X+T)=sin(A*X^2+BX+T).
Hier haben wir einen Ansatzpunkt. Polynom unter dem Vorzeichen des Sinus. Regression ausführen.... usw. - Ich hoffe, ich habe das deutlich erklärt. Ich würde Ihnen gerne ein Programm in Matlab erstellen, aber ich habe keine Zeit, das müssen Sie schon selbst machen.
Lassen Sie mich kurz erklären, wozu das gut sein soll. Ich habe eine Idee für TC auf der Grundlage eines Prädikats. Von den mir bekannten und mehr oder weniger verfügbaren sind Fourier und Regression. Angewandt auf Fourier. Die zugrunde liegende Annahme ist, dass die Parameter stationär sind. Bei einer normalen Sinuswelle sieht alles gut aus.
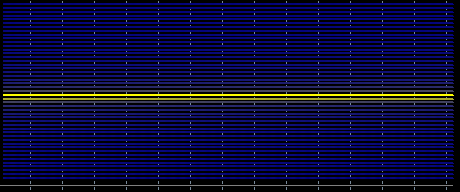
Nimmt man jedoch eine gleichmäßig variierende Periode, so wird das Spektrum verschmiert
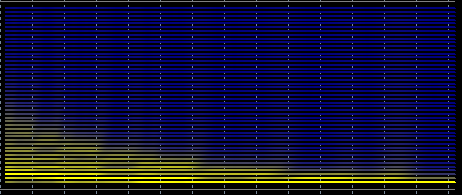
und daher kann man keine angemessene Vorhersage treffen.
Ich konnte auch nichts Gutes über Regression herausfinden.
Deshalb müssen wir nach anderen Methoden suchen, die "anpassungsfähiger" oder so ähnlich sind. Das ist es, was ich wissen wollte.
Sie haben eine glatte Kurve. Daher sind die Methoden der Differentialanalyse auf sie anwendbar. Auch ohne zu wissen, dass es sich um einen Sinus mit variabler Periode handelt, kann man eine Taylorreihenentwicklung unter Beibehaltung der ersten Terme verwenden. Anschließend können Sie damit den Wert einer künftigen Referenz vorhersagen, indem Sie einige frühere Terme in die Formel einsetzen. Ich kann Ihnen versichern, dass das Ergebnis Sie mit seiner Vorhersagegenauigkeit verblüffen wird. Der Fehler ist gleich Null.
Bei Preisreihen funktioniert das nicht, denn bei der Zerlegung in RF erhält man PDF, und man muss nicht eine Zählung vorwärts vorhersagen, sondern die Anzahl der Zählungen, die in die PDF-Skala passt, und da steigt der Vorhersagefehler dramatisch an.
Die Natur lässt sich nicht täuschen.
Und all dies wird bei Preisreihen nicht funktionieren, denn wenn man in RF zerlegt, erhält man eine FZ, und man muss nicht eine Zählung vorwärts vorhersagen, sondern die Anzahl der Zählungen, die auf die Skala der FZ passen, und in diesem Abstand wird der Vorhersagefehler dramatisch zunehmen.
Die Natur lässt sich nicht täuschen.
Das ist verständlich. Es kann jedoch davon ausgegangen werden, dass sich die Parameter im Laufe der Zeit nicht ändern. Mit dem oberen Bild wollte ich zeigen, dass das Ergebnis nicht nur durch Nicht-Stationarität, sondern auch durch eine ungeeignete Methode schlecht sein kann.
Das ist klar. Es ist jedoch möglich, davon auszugehen, dass sich die Parameter über einen bestimmten Zeitraum nicht ändern. Mit dem oberen Bild wollte ich zeigen, dass das Ergebnis nicht nur durch Nicht-Stationarität, sondern auch durch eine ungeeignete Methode schlecht sein kann.
Die Hypothese eines stationären Marktes hat sich nie bestätigt. Daher kann nicht davon ausgegangen werden, dass die Parameter über jeden noch so kleinen Zeithorizont konstant bleiben.
Lassen Sie mich kurz erklären, wozu das gut sein soll. Ich habe eine Idee für TC auf der Grundlage eines Prädikats. Von den mir bekannten und mehr oder weniger verfügbaren sind Fourier und Regression. Angewandt auf Fourier. Die zugrunde liegende Annahme ist, dass die Parameter stationär sind. Bei einer normalen Sinuswelle sieht alles gut aus.
Nimmt man jedoch eine gleichmäßig variierende Periode, so wird das Spektrum verschmiert
und daher kann man keine angemessene Vorhersage treffen.
Ich konnte auch nichts Gutes über Regression herausfinden.
Deshalb müssen wir nach anderen Methoden suchen, die "anpassungsfähiger" sind oder ähnliches. Das ist es, was ich wissen wollte.
Was kann ein Wavelet leisten?
ZS: Ich habe eine .dll mit Code von BaseGroup.ru für MT5 gemacht, aber ich habe noch keine praktische Anwendung gefunden http://imglink.ru/pictures/18-01-12/4e3891b89673e8f79e194b5a86a25d41.jpg
Die Hypothese eines stationären Marktes hat sich nie bestätigt. Es kann daher nicht davon ausgegangen werden, dass die Parameter über jeden noch so kleinen Zeithorizont konstant bleiben.
Ich spreche nicht von vollständiger Stationarität, aber vielleicht gibt es Abschnitte, in denen die Parameter mehr oder weniger stabil sind. Wie sollte man sonst erklären, dass die Strategien eine Zeit lang funktionieren können. Es gibt einen Ansatz, bei dem man mehrere Strategien entwickelt und zwischen ihnen wechselt.
www.https://www.mql5.com/ru/forum/127297 Hier gibt es indirekte Hinweise auf eine zeitliche Vorhersagbarkeit.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Es gibt ein Bild wie dieses:
Mit welcher Methodik kann eine solche Serie extrapoliert werden?
Könnte jemand dies für ein Experiment in ein neuronales Netz eingeben?