再次感谢 Stanislav!终于有一篇关于使用本机矩阵的神经网络的文章被写出来了....。
顺便说一下。就在今天,我发现文档中有一个关于 ML 的新模块。

- www.mql5.com
有两个方面很重要:
1.执行,技术部分,普遍性,即使是成熟的程序员也会称赞。在这里,我确实不能、不会也没有试图批评代码。我说的是其他方面:
2.测试。作者指出,他的所有模型都能正常工作。事实上,当您按下测试器中的 "Start"(开始)按钮时,会随机出现一张未来 2 周的图片,在 10 次按下中有 5 次--梅花,5 次--盈利。当然,如果你把这样的东西放在真实的 - 你的车厂 50/50 的可行性。事实并非如此。在我询问这是什么原因以及如何解决时,作者说应该是这样的,这是模型的原理。
两个月后,我试图启动这些网络,但它们无法在 NVIDIA 上运行,多亏Aleksey Vyazmikin 重写了作者的代码,一切才得以在 3080 上运行。最后 - 无法运行的模型。这让人倍感不快。
但如果我冒犯/冒犯了您,我向您道歉,我并没有这样的目的。
matrix temp; if(!outputs[n].Derivative(temp, of))
在反向传播中,导数函数期望接收x,而不是x 的 激活(除非他们最近对其适用的激活函数进行了更改)。
下面是一个例子:
#property version "1.00" int OnInit() { //--- double values[]; matrix vValues; int total=20; double start=-1.0; double step=0.1; ArrayResize(values,total,0); vValues.Init(20,1); for(int i=0;i<total;i++){ values[i]=sigmoid(start); vValues[i][0]=start; start+=step; } matrix activations; vValues.Activation(activations,AF_SIGMOID); //打印 sigmoid for(int i=0;i<total;i++){ Print("sigmoidDV("+values[i]+")sigmoidVV("+activations[i][0]+")"); } //衍生产品 matrix derivatives; activations.Derivative(derivatives,AF_SIGMOID); for(int i=0;i<total;i++){ values[i]=sigmoid_derivative(values[i]); Print("dDV("+values[i]+")dVV("+derivatives[i][0]+")"); } //--- return(INIT_SUCCEEDED); } double sigmoid(double of){ return((1.0/(1.0+MathExp((-1.0*of))))); } double sigmoid_derivative(double output){ return(output*(1-output)); }
还有一些激活函数可以在激活和求导过程中输入更多信息,例如 elu
Derivative(output,AF_ELU,alpha); Activation(output,AF_ELU,alpha);
请允许我简化一下......:
#property version "1.00" int OnInit() { //--- //假设 x 是上一层的输出 (*) 节点的权重 // the value that goes in activation . double x=3; //我们根据下面的公式得到 sigmoid double activation_of_x=sigmoid(x); //对于导数,我们的做法是 double derivative_of_activation_of_x=sigmoid_derivative(activation_of_x); //我们用矩阵向量来实现这一点 vector vX; vX.Init(1); vX[0]=3; //我们为激活创建一个向量 vector vActivation_of_x; vX.Activation(vActivation_of_x,AF_SIGMOID); //我们为派生创建一个向量 vector vDerivative_of_activation_of_x,vDerivative_of_x; vActivation_of_x.Derivative(vDerivative_of_activation_of_x,AF_SIGMOID); vX.Derivative(vDerivative_of_x,AF_SIGMOID); Print("NormalActivation("+activation_of_x+")"); Print("vector Activation("+vActivation_of_x[0]+")"); Print("NormalDerivative("+derivative_of_activation_of_x+")"); Print("vector Derivative Of Activation Of X ("+vDerivative_of_activation_of_x[0]+")"); Print("vector Derivative Of X ("+vDerivative_of_x[0]+")"); //你正在对 x 的激活进行矢量导数运算,这会返回错误的值 //向量矩阵希望您发送的是 x 而不是激活 (x) //--- return(INIT_SUCCEEDED); } double sigmoid(double of){ return((1.0/(1.0+MathExp((-1.0*of))))); } double sigmoid_derivative(double output){ return(output*(1-output)); }
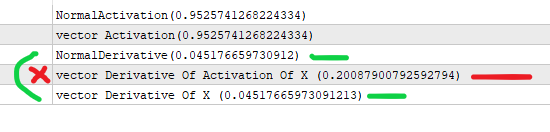
我明白你的意思了。事实上,sigmoid 导数是通过 "y "来表示的,即通过x 点的 sigmoid 值,也就是 y(x):y'(x) = y(x)*(1-y(x)) 。文章中的代码正是这样实现的。
您的测试脚本计算 "导数 "时输入的是 x,而不是 y,因此数值不同。
是的,但激活值是传递给导数函数的,而导数函数期望的是激活前的值。我就是这个意思。
你忽略了一点,正确的值是以 x 作为输入的值(根据 mq 函数本身,这才是正确的值)。
您没有将 output_of_previous * 权重存储在某个地方(我认为),而这正是推导函数应该发送的值(根据 mq 函数本身,我再次强调这一点)。

新文章 利用 MQL5 矩阵的反向传播神经网络已发布:
本文讲述在 MQL5 中利用矩阵来应用反向传播算法的理论和实践。 它还提供了现成的类,以及脚本、指标和智能交易系统的示例。
正如我们将在下面看到的,MQL5 提供了大量的内置激活函数。 函数的选择应基于特定问题(回归、分类)。 通常,可以选择几个函数,然后经由验正找到最优的一个。
流行的激活函数
激活函数可以具有不同的数值范围、有限或无限。 特别是,sigmoid(3) 将数据映射到范围 [0,+1],这对于分类问题更好;而双曲正切将数据映射到范围 [-1,+1],假设范围,推测这对于回归和预测问题更佳。
作者:Stanislav Korotky