从理论到实践 - 页 534 1...527528529530531532533534535536537538539540541...1981 新评论 multiplicator 2018.09.05 22:50 #5331 Vladimir:谢谢你的链接,我忘乎所以地寻找相关的想法了。我认为你不需要像那里一样,从R函数的角度来处理这个问题。用常规手段进行处理。 直接从半径为R的圆的方程,中心坐标为Xc,Yc,忽略单位(数字、路线、距离)的意义的丧失R^2 = (X-Xc)^2 + (Y-Yc)^2我们做了一个数字为i(Xi=i)的点的不一致的函数。这是从点(Xi,Yi)到中心Xc,Yc和半径R之间的距离之差。Di=((Xi-Xc)^2+(Yi-Yc)^2)^0.5-R。Di和的平方相加,得到要最小化的目标函数。有三个参数需要变化:R、Xc、Yc。最外侧(第一个和最后一个)的点比中间的点(没有相邻的)影响要小,我认为把相应的Di^2乘以2比较好。为了达到强调最后几个点的拟合目的,你还可以通过多设置一列权重来发挥最后几个点的权重。 如果不是直的,就必须考虑到测量单位。为了使X和Y在距离计算中的影响几乎相同(而R受两者影响),有必要不取i数作为X,而是取同一数字乘以排列比例,使X和Y的范围大小接近。 P.S. 事实证明,sernam.ru非常巧妙地摆脱了对侵犯版权的指控,只公布了部分书籍的文本,没有指定输出数据,特别是书名。在sernam.ru上可以找到在互联网上其他地方找不到的文本。 当然,谢谢你的时间...... 我想明白了,我需要用Di = ((Xi-Xc)^2 + (Yi-Yc)^2)^0.5 - R来最小化。 然后就需要通过游戏来绘制发现的圆。 该方程式将是。 y=(R^2-(X-Xc)^2)^0.5+Yc弗拉基米尔。 还有一件事,我在Excel中试过圆弧回归和多项式回归,结果没有什么不同。 所以,不要在这个方向上浪费你的时间。 虽然,你可以建立一个基于弧线而不是直线的指标,就像mashka.也许它会比sma效果更好。弗拉基米尔。这是我采取的公式。 弧的一般方程。(x - L)^2+ (y + (R - H))^2 = R^2 y = sqrt(R^2 - (x - L)^2) - (R - H) , 其中R的公式在图中。 但它只适用于正平面。在实验中,我采取了一个位于正平面的 "弧形价格通道"。 附加的文件: 95no_3.zip 27 kb From theory to practice DoEasy 函数库中的图形(第八十部分): 几何动画框 对象类 Box-Cox 变换 multiplicator 2018.09.06 00:05 #5332 顺便说一下,在监测网站上,现在盈利能力领先的是一个名为 "polynom "的账户。结果是:存款增加了660倍。这不是为了做广告(我不能做广告,所有者是一个来自奥地利的女孩),这也许是为了帮助你找到正确的道路。 也许这只是一个漂亮的名字选择... Vladimir 2018.09.06 01:16 #5333 RRR5: ... 但这只适用于正平面。在实验中,我采取了一个 "弧形的价格通道",它位于正平面。 什么是 "正平面"? multiplicator 2018.09.06 01:53 #5334 Vladimir:什么是 "正平面"? 好吧,这对这个弧线是有效的。 但不是这个弧度。 Vladimir 2018.09.06 02:22 #5335 RRR5: 好吧,对于像这样的弧线,它将会发挥作用。 但不是为了这一次。 RRR5,你画得很快。我想知道,用什么? multiplicator 2018.09.06 02:27 #5336 Vladimir: RRR5,你画得很快。我想知道,用什么? 用一品脱)))。 Nikolai Semko 2018.09.06 07:10 #5337 我在这里读到了多项式、ANC、各种近似方法、预测能力等......。 有些人相信预测,有些人不相信。 但我希望找到的东西,我从未见过。 为了试图解释我的意思,我将借助于宇宙中的重力来进行类比。 下面是我录制的gif动画,请看。 为自己回答这个问题。是否有可能预测每个物体的轨迹? 嗯,你当然可以。 但前提是你必须知道每个物体此刻的信息:它的质量、当前位置和运动方向、它出现的时间和消失的时间。 然后,这是一个数学和计算的问题,基本上只使用一个公式(对于远离光速的速度的经典力学的一个变种)。 该方案本身就是一个重力干扰器,就在这里。你可以用它来玩。 也有必要了解,即使是我们的地球也不是在一个封闭的圆圈中运动,实际上是一个三维的正弦波(螺旋)。 这个视频清楚地展示了这一点。 那么,如果我们没有关于所有对象的信息呢? 我们能在过去只知道轨迹本身的情况下预测轨迹吗? 这就是乐趣的开始。 如果有人说这是不可能的,那么这个答案就是错误的。肯定的答案也是错误的。 这个问题的解决方案只会是概率性的。 必须从相反的方向来解决这个问题。根据过去的轨迹,我们必须首先计算出主要 "团块 "物体的概率轨迹和它们的质量。然后预测可能的轨迹的概率模型。 这就是人工智能的基本任务--模式识别。 据我所知,这就是马克西姆-德米特里夫斯基所说的。 大约六年前,我在KB上发表了我在这个领域的第一个发展:https://www.mql5.com/ru/code/10882。 我只是用一个1度的多项式(线性回归)来进行通道识别。此后,我在这方面有了很大的进步。但我没有发表任何东西,也不会发表,原因很明显。我只为探究的人提供提示。 寻找线性通道实质上就是寻找这些引力质量的中心。 任何仪器(符号)中通常有5-10个这样的中心(通道)。为了预测价格,应该同时考虑到所有这些因素。只有在这种情况下,预测上升或下降的准确性才会远远高于50%。 但每个人都试图找到一组特殊的数字,并天真地认为它们可以预测未来。 问题是这个 "数组 "是活的,动态的,它不断变化,以及与物质引力相类似的一组物体的局部质心位置的变化。 而问题被简化为找到这个 "数组 "的变化规律,甚至找到规律本身的变化规律:) ) 理想情况下,这个 "一组数字 "应该在每次打勾时重新计算。这正是我不止一次说过,许多人所谓的优化,找到一个特定的 "数字集",是对历史数据的微不足道的修补。 我认为与重力的比喻非常贴切。在市场上,重力是由货币创造的。有些人将带着100美元进去,有些人带着几十亿进去。同样的重力定律也适用于此,甚至与我上面给出的公式相同。吸引力与距离的平方成反比,与质量成正比。因此,2度的多项式回归(抛物线)是最合适的工具。尽管使用双曲线会更符合逻辑,因为两个引力体的相互作用是根据双曲线的规律进行的。但是,事实上,抛物线在计算上要方便得多,而且抛物线和双曲线在最重要的区间上也非常相似。 你可以在这里 清楚地看到它。红线是抛物线,蓝线是双曲线。 货币的引力和天体的引力之间的主要区别是,货币可以突然出现和突然消失,产生强大的引力波动。但是要计算这个事件,而且有这样的事情,就是渠道崩溃。 分形、分形结构、其图形图像+画布 Georgiy Merts 2018.09.06 07:24 #5338 Nikolai Semko:这个问题的解决方案只会是概率性的。 这个问题必须反向解决。从过去的轨迹中,我们必须首先计算出主要 "团块 "物体的概率轨迹和它们的质量。然后预测可能的轨迹的概率模型。恐怕这里的 "概率解决方案 "将是给定空间中任何轨迹的整个集合--而该解决方案的价值是什么? 这就像声称 "很有可能 "欧洲美元今年不会出现负值,不超过100。请注意,这一论断的概率接近100%。但你会从这样的 "预测 "中得到很多好处吗? 在概率论中证明,当一个物体的状态受到许多独立力量的影响时,该状态的概率开始服从高斯定律。然而,价格的走向和价值并不服从这种分布,原因很简单,市场参与者的投入和产出是相互依赖的。 Georgiy Merts 2018.09.06 07:29 #5339 RRR5: понял, что минимизировать нужно по формуле Di = ((Xi-Xc)^2 + (Yi-Yc)^2)^0.5 - R. ... 但它只适用于正平面。 在实验中,我采取了一个 "弧形的价格通道",它位于正平面内。 我还是不明白你为什么不喜欢MNC。绘制上述任何一条曲线都是可以的。 Natalja Romancheva 2018.09.06 07:36 #5340 Uladzimir Izerski:我喜欢在小型TF上工作,但我不喜欢这些煞风景的事情。 你如何预测它们? 16:00身份证加拿大 银行的附带声明16:00身份证利率决定1,50%1,50%1,50% 1...527528529530531532533534535536537538539540541...1981 新评论 您错过了交易机会: 免费交易应用程序 8,000+信号可供复制 探索金融市场的经济新闻 注册 登录 拉丁字符(不带空格) 密码将被发送至该邮箱 发生错误 使用 Google 登录 您同意网站政策和使用条款 如果您没有帐号,请注册 可以使用cookies登录MQL5.com网站。 请在您的浏览器中启用必要的设置,否则您将无法登录。 忘记您的登录名/密码? 使用 Google 登录
谢谢你的链接,我忘乎所以地寻找相关的想法了。我认为你不需要像那里一样,从R函数的角度来处理这个问题。用常规手段进行处理。
直接从半径为R的圆的方程,中心坐标为Xc,Yc,忽略单位(数字、路线、距离)的意义的丧失
R^2 = (X-Xc)^2 + (Y-Yc)^2
我们做了一个数字为i(Xi=i)的点的不一致的函数。这是从点(Xi,Yi)到中心Xc,Yc和半径R之间的距离之差。
Di=((Xi-Xc)^2+(Yi-Yc)^2)^0.5-R。
Di和的平方相加,得到要最小化的目标函数。有三个参数需要变化:R、Xc、Yc。最外侧(第一个和最后一个)的点比中间的点(没有相邻的)影响要小,我认为把相应的Di^2乘以2比较好。为了达到强调最后几个点的拟合目的,你还可以通过多设置一列权重来发挥最后几个点的权重。
如果不是直的,就必须考虑到测量单位。为了使X和Y在距离计算中的影响几乎相同(而R受两者影响),有必要不取i数作为X,而是取同一数字乘以排列比例,使X和Y的范围大小接近。
P.S. 事实证明,sernam.ru非常巧妙地摆脱了对侵犯版权的指控,只公布了部分书籍的文本,没有指定输出数据,特别是书名。在sernam.ru上可以找到在互联网上其他地方找不到的文本。
我想明白了,我需要用Di = ((Xi-Xc)^2 + (Yi-Yc)^2)^0.5 - R来最小化。
然后就需要通过游戏来绘制发现的圆。
该方程式将是。
y=(R^2-(X-Xc)^2)^0.5+Yc
所以,不要在这个方向上浪费你的时间。 虽然,你可以建立一个基于弧线而不是直线的指标,就像mashka.也许它会比sma效果更好。
这是我采取的公式。
弧的一般方程。
(x - L)^2+ (y + (R - H))^2 = R^2
y = sqrt(R^2 - (x - L)^2) - (R - H) , 其中R的公式在图中。
但它只适用于正平面。在实验中,我采取了一个位于正平面的 "弧形价格通道"。
也许这只是一个漂亮的名字选择...
RRR5:
...
但这只适用于正平面。在实验中,我采取了一个 "弧形的价格通道",它位于正平面。
什么是 "正平面"?
什么是 "正平面"?
但不是这个弧度。
好吧,对于像这样的弧线,它将会发挥作用。
但不是为了这一次。
RRR5,你画得很快。我想知道,用什么?
我在这里读到了多项式、ANC、各种近似方法、预测能力等......。
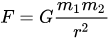
有些人相信预测,有些人不相信。
但我希望找到的东西,我从未见过。
为了试图解释我的意思,我将借助于宇宙中的重力来进行类比。
下面是我录制的gif动画,请看。
为自己回答这个问题。是否有可能预测每个物体的轨迹?
嗯,你当然可以。
但前提是你必须知道每个物体此刻的信息:它的质量、当前位置和运动方向、它出现的时间和消失的时间。
然后,这是一个数学和计算的问题,基本上只使用一个公式(对于远离光速的速度的经典力学的一个变种)。
该方案本身就是一个重力干扰器,就在这里。你可以用它来玩。
也有必要了解,即使是我们的地球也不是在一个封闭的圆圈中运动,实际上是一个三维的正弦波(螺旋)。
这个视频清楚地展示了这一点。
那么,如果我们没有关于所有对象的信息呢?
我们能在过去只知道轨迹本身的情况下预测轨迹吗?
这就是乐趣的开始。
如果有人说这是不可能的,那么这个答案就是错误的。肯定的答案也是错误的。
这个问题的解决方案只会是概率性的。
必须从相反的方向来解决这个问题。根据过去的轨迹,我们必须首先计算出主要 "团块 "物体的概率轨迹和它们的质量。然后预测可能的轨迹的概率模型。
这就是人工智能的基本任务--模式识别。
据我所知,这就是马克西姆-德米特里夫斯基所说的。
大约六年前,我在KB上发表了我在这个领域的第一个发展:https://www.mql5.com/ru/code/10882。 我只是用一个1度的多项式(线性回归)来进行通道识别。此后,我在这方面有了很大的进步。但我没有发表任何东西,也不会发表,原因很明显。我只为探究的人提供提示。
寻找线性通道实质上就是寻找这些引力质量的中心。
任何仪器(符号)中通常有5-10个这样的中心(通道)。为了预测价格,应该同时考虑到所有这些因素。只有在这种情况下,预测上升或下降的准确性才会远远高于50%。
但每个人都试图找到一组特殊的数字,并天真地认为它们可以预测未来。
问题是这个 "数组 "是活的,动态的,它不断变化,以及与物质引力相类似的一组物体的局部质心位置的变化。 而问题被简化为找到这个 "数组 "的变化规律,甚至找到规律本身的变化规律:) )
理想情况下,这个 "一组数字 "应该在每次打勾时重新计算。这正是我不止一次说过,许多人所谓的优化,找到一个特定的 "数字集",是对历史数据的微不足道的修补。
我认为与重力的比喻非常贴切。在市场上,重力是由货币创造的。有些人将带着100美元进去,有些人带着几十亿进去。同样的重力定律也适用于此,甚至与我上面给出的公式相同。吸引力与距离的平方成反比,与质量成正比。因此,2度的多项式回归(抛物线)是最合适的工具。尽管使用双曲线会更符合逻辑,因为两个引力体的相互作用是根据双曲线的规律进行的。但是,事实上,抛物线在计算上要方便得多,而且抛物线和双曲线在最重要的区间上也非常相似。
你可以在这里 清楚地看到它。红线是抛物线,蓝线是双曲线。
货币的引力和天体的引力之间的主要区别是,货币可以突然出现和突然消失,产生强大的引力波动。但是要计算这个事件,而且有这样的事情,就是渠道崩溃。
这个问题的解决方案只会是概率性的。
这个问题必须反向解决。从过去的轨迹中,我们必须首先计算出主要 "团块 "物体的概率轨迹和它们的质量。然后预测可能的轨迹的概率模型。
恐怕这里的 "概率解决方案 "将是给定空间中任何轨迹的整个集合--而该解决方案的价值是什么?
这就像声称 "很有可能 "欧洲美元今年不会出现负值,不超过100。请注意,这一论断的概率接近100%。但你会从这样的 "预测 "中得到很多好处吗?
在概率论中证明,当一个物体的状态受到许多独立力量的影响时,该状态的概率开始服从高斯定律。然而,价格的走向和价值并不服从这种分布,原因很简单,市场参与者的投入和产出是相互依赖的。
RRR5:
понял, что минимизировать нужно по формуле Di = ((Xi-Xc)^2 + (Yi-Yc)^2)^0.5 - R.
...
但它只适用于正平面。 在实验中,我采取了一个 "弧形的价格通道",它位于正平面内。
我还是不明白你为什么不喜欢MNC。绘制上述任何一条曲线都是可以的。
我喜欢在小型TF上工作,但我不喜欢这些煞风景的事情。
你如何预测它们?