"Ticaret için kombinatorik ve olasılık teorisi (Bölüm II): Evrensel fraktal" makalesi için tartışma
Eğer mümkünse, bu makalenin yazarından aşağıdaki argümanları dikkate almasını rica ediyorum:
Şimdiye kadar altın oran prensibinin tam bir olaylar grubu oluşturan fraktal-probabilistik zincirler inşa etmek için kullanılabileceğini görüyorum, ancak böyle bir yaklaşımın ne verebileceğini açıkçası göremiyorum. Altın oran aynı zamanda fibo serisi ile de bağlantılı gibi görünüyor ama yine nasıl uygulanabileceğini ve ne için kullanılabileceğini göremiyorum, eğer fikirleriniz varsa buraya yazabilirsiniz, burada bir artı olacağını düşünüyorum. Ve böylece genel olarak bu süreçler kafamda zaten oluştu, genel olarak daha karmaşık formüller türetmek için gereken tek şey bu. Şimdiye kadar elde edilen fraktallar görevlerini yerine getiriyor. Orada her şey karmaşıktan basite doğru gidiyor ve böyle devam ediyor. Altın oranın uygulamasını düşünebilirim, ama nasıl yararlı olacağını göremiyorum. Fibo serileri de, herkes fibo-fibo diyor ... Ololo, zekice bir kelime duyuyorlar ve papağan gibi tekrarlıyorlar. Her zaman matematiksel bir prensibin belirli bir probleme karşılık geldiği gerçeğinden hareket ederim ve her zaman bir süre sonra herhangi bir probleme bir çözüm bulurum. Çözüm aracı süreç içinde seçilir, beyin kendisi bulur ve mümkünse kulakta olan bir şeyle benzerlikler bulur. Yani önce neyi bulmamız gerektiğini belirliyoruz, sonra da sorunu çözmenin yollarını arıyoruz. Spesifik problemleri duymak daha çok ilgimi çekerdi, bu tür çözümleri ayrı bir makale haline getirebilirsiniz, ilginç ve eğlenceli olur diye düşünüyorum. Bu problemler çerçevesinde altın oranı veya başka herhangi bir şeyi uygulayabiliriz, yeter ki sonuç gerçekten gerekli olsun ve birilerine somut bir fayda sağlasın. Yani öneriler yazabilirsiniz.
Eğer mümkünse, bu makalenin yazarından aşağıdaki argümanları dikkate almasını rica ediyorum:
Bu sadece her yerde fibo ve ZS olduğu iddia edilen basmakalıp bir efsanedir....
Komik olan şu ki, herhangi bir saksıyı alıp iyice bükerseniz içinde hem fibo hem de altın oran, pi ve e ve daha birçok şey bulabilirsiniz....
Bu sadece sözde fibo ve ZS'nin her yerde ve her zaman var olduğuna dair basmakalıp bir efsane...
İşin komik yanı, herhangi bir kabı alıp iyice döndürürseniz içinde fibo ve altın oran ve pi sayısı ve e sayısı ve daha birçok şey bulabilirsiniz....
Fiba (aynı zamanda birçok insanın farkına varmadığı altın orandır) son derece kolay bir şekilde aranır, yani görülür. Çünkü onlar üsteldir. Onlar da toplamlardır... Genel olarak, okuldaki temel şeylerden (!!!) uzun süre bahsedebilirsiniz, ama faydasızdır.
Bu şekilde de yapabilirsiniz:
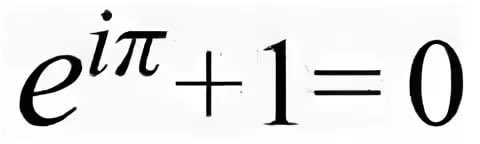
güzel, gizemli... FIBO'nun Fourier ile bağlantısı... bir bardakta dünya sabitleri... ve diğer şeyler.
Bu sadece sözde fibo ve ZS'nin her yerde ve her zaman var olduğuna dair basmakalıp bir efsane...
İşin komik yanı, herhangi bir kabı alıp iyice döndürürseniz, içinde fiboyu ve altın oranı ve pi sayısını ve e sayısını ve daha birçok şeyi bulabilirsiniz....
Başınızın üzerine koyarsanız tencerede baş ve omuzları da bulabilirsiniz).
Fibo ve ZS'nin her yerde olduğu.... sadece basmakalıp bir efsanedir.
Komik olan şu ki.... eğer herhangi bir kabı alır ve iyice bükerseniz içinde fibo ve altın oran ve pi ve e ve daha birçok şey bulabilirsiniz.
Daha fazla katılamazdım ))) gerçekten doğru. Tüccarlar hiç olmayan yerde gizli bir anlam aramaya çok düşkündür). Ben de insanlara aynı şeyi anlatmaya çalışıyorum ama gerçeği söylemeden bunu nasıl yapacağımı bilmiyorum ve gerçek acımasızdır). Bir sorun olduğu ve bir dizi olası çözümün bulunduğu ve bunun dışındaki her şeyin zaman kaybı olduğu noktasına geldim. Bir çözüme ulaşmak için öncelikle problemi net bir şekilde ortaya koymalı ve olası çözüm yolları hakkında en azından yüzeysel bir fikre sahip olmalısınız, eğer böyle bir yol yoksa, o zaman yukarıda anlatılanlar başlar, Fibonacci, Euler'in formülleri ve diğer çok güzel ama o kadar çok işe yaramaz saçmalıklar ki istemeden satır aralarını okumaya başlarsınız. Her aracın kendi görevi vardır. Bu bağlamda, ayrıntılara (spesifik görevlere) inmeyi öneriyorum.
Şimdiye kadar altın oran prensibinin tam bir olay grubu oluşturan fraktal olasılık zincirleri oluşturmak için kullanılabileceğini görüyorum, ancak bu yaklaşımın ne yapabileceğini açıkçası göremiyorum. Altın oran aynı zamanda fibo serileriyle de bağlantılı gibi görünüyor ama yine nasıl uygulanabileceğini ve ne için kullanılabileceğini göremiyorum, eğer fikirleriniz varsa buraya yazabilirsiniz, burada bir artı olacağını düşünüyorum. Ve böylece genel olarak bu süreçler kafamda zaten oluştu, genel olarak daha karmaşık formüller türetmek için gereken tek şey bu. Şimdiye kadar elde edilen fraktallar görevlerini yerine getiriyor. Orada her şey karmaşıktan basite doğru gidiyor ve böyle devam ediyor. Altın oranın uygulamasını düşünebilirim, ama nasıl yararlı olacağını göremiyorum. Fibo serileri de, herkes fibo-fibo diyor ... Ololo, zekice bir kelime duyuyorlar ve papağan gibi tekrarlıyorlar. Her zaman matematiksel bir prensibin belirli bir probleme karşılık geldiği gerçeğinden hareket ederim ve her zaman bir süre sonra herhangi bir probleme bir çözüm bulurum. Çözüm aracı süreç içinde seçilir, beyin kendisi bulur ve mümkünse kulakta olan bir şeyle benzerlikler bulur. Yani önce neyi bulmamız gerektiğini belirliyoruz, sonra da sorunu çözmenin yollarını arıyoruz. Spesifik problemleri duymak daha çok ilgimi çekerdi, bu tür çözümlerle ayrı bir makale yapabilirsiniz, ilginç ve eğlenceli olur diye düşünüyorum. Bu problemler çerçevesinde altın oranı veya başka herhangi bir şeyi uygulayabiliriz, yeter ki sonuç gerçekten gerekli olsun ve birilerine somut bir fayda sağlasın. Yani öneriler yazabilirsiniz.
1. Belki herkes bu "ololo" yu duymuştur, ancak fibo hakkında yazmadım, çünkü fibo seviyelerini "çekmeyi" tavsiye etmiyorum, ancak doğru hesaplanırlarsa kullanılabilirler, ancak Elliott dalgalarıyla birlikte.
Elbette hepsi bu kadar değil, bu işin ne kadar zaman alıcı ve zahmetli olduğunun farkındasınızdır, ancak bu başlığı açmamın bir nedeni var. Bana bağlı olan her şeyi yapmaya çalışacağım ve genel olarak bu tür sorular, dürüst olmak gerekirse, bütün bir enstitü olmasa bile, matematikçiler ve programcılardan oluşan bir ekip tarafından ele alınmalıdır. Bir kişi buna karşı ne yapabilir? Süper bir beyniniz olsa bile, işlenecek o kadar çok veri var ki çıldırabilirsiniz. Zamanım ve yeteneklerimle orantılı olan görevleri belirlemeye çalışıyorum, evet daha fazlasını yapabilirim ama bu artık bana bağlı değil. Zaman en değerli kaynaktır. Karmaşık analizlerle ve tam bir adanmışlıkla ilgilenen insanlar varsa bunu yapmaktan mutluluk duyarım. Yine de branş devam edecek ve elimden geldiğince yeni bir şeyler anlatmaya çalışacağım.
Doğadaki altın oranın evrenselliği hakkındaki efsane o kadar büyümüştür ki, insanlar gerçek kontrollerle kendilerini rahatsız bile etmezler, bütünün ve parçalarının oranı fikrinin güzelliğinin cazibesine kapılırlar, ama aslında öyle değildir:
- Yumuşakça-nautilus kabukları (genellikle WD'nin büyüsü hakkındaki makalelerde gösterilir) popüler görüşün aksine WD'ye karşılık gelmez.
- Leonardo Da Vinci'nin ünlü "Vitruvius Adamı" çizimindeki insan vücudunun oranları gerçek insanlarla ilişkili olarak gözlemlenmemektedir.
- Parthenon, Piramitler ve diğer nesneler çok yanlış bir şekilde RS'ye karşılık gelmektedir (mistisizm severler tarafından çizilmiştir).
- EQ'nun güzellik algısının temeli olup olmadığını ortaya çıkarmak amacıyla yapılan nesnel psikolojik araştırmalar başarılı bir şekilde başarısız olmuştur.
- Son olarak, ticarette seviyelerin bozulması/reddedilmesine ilişkin nicel testler de EQ'nun özellikle önemli bir şey olduğunu göstermemektedir.
Piyasaların bazen (anahtar kelime BAŞKA BİR ZAMAN) fibo seviyelerini güzel bir şekilde geri çekebilmesinin / kırabilmesinin tek nedeni, çok sayıda teknik tüccarın fibo seviyelerine olan kolektif inancıdır (kendi kendini gerçekleştiren bir kehanet), eğer duraklarını / limitlerini toplu olarak oraya koyarlarsa, ancak bu bile muhtemelen işe yaramayacaktır çünkü profesyonel katılımcılar, büyük kurumsal oyuncular başka bir temelde işlem yapacaklardır, Fibo seviyesinin kırılması/tersine dönmesi rastlantısal olabilir, ancak EQ'ya inananlar için bu kesinlikle inançlarının bir teyidi olacaktır.
Stanford Üniversitesi'nde Matematik Profesörü olan Keith Devlin bunu basitçe açıklıyor: "..... Çoğu insan matematikten anlamaz ve altın oran gibi bir formülün karmaşık bir sisteme nasıl uygulandığını bile anlayamaz, bu yüzden kendilerini de test edemezler. İnsanlar altın oranı her yerde, doğada ve en sevdikleri nesnelerde gördüklerini düşünürler ama bunu kanıtlayamazlar. Evrenin çeşitli nesnelerinde anlam bulmaya yönelik doğal arzularının kurbanıdırlar, ancak matematik okuryazarlıklarının olmaması nedeniyle tespit ettikleri kalıpların yanıltıcı olduğunu fark edemezler."
İnsanlar kendilerini basit bir açıklama aramaya programlar (zombi) ve bu inancı sürdürmek için çabalarlar, ticaret de dahil olmak üzere dini düşüncenin özü budur...
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz
Yeni makaleye göz atın: Ticaret için kombinatorik ve olasılık teorisi (Bölüm II): Evrensel fraktal.
Bu makalede fraktalları incelemeye devam edeceğiz ve tüm materyali özetlemeye özellikle dikkat edeceğiz. Bunu yapmak için, daha önceki tüm gelişmeleri, ticarette pratik uygulama için uygun ve anlaşılabilir olacak kompakt bir forma getirmeye çalışacağım.
Bir önceki makalede türettiğimiz yapı kurallarını kullanalım ve bir fraktalın nasıl inşa edildiğini anlamak için onları tamamlayalım. Buna ek olarak, formüllerimde küçük bir hata buldum, bu nedenle sınırların aşağı veya yukarı doğru asimetrikleştirilmesi imkansızdı. Türetilen formüllerin doğru olduğu ortaya çıktı ve bu nedenle kesinlikle herhangi bir fraktal için çalışıyorlar. Aslında, bu kesinlikle herhangi bir fraktal uygulamak için bir fonksiyondur. Tüm olası fraktallar, genel bir fraktalın özel bir durumudur. Yukarıda tanımlanan üç fraktal tipini ele alırsak, bu üç özel durumun uygulanması için genel fraktalın koşulları aşağıdaki gibi olacaktır:
Şematik olarak, bu üç fraktal türü şu şekilde görünür:
İdeal olarak, "S" sonsuza doğru gitmelidir. Aşağıdaki değişkenler önceki makalemde açıklanmamıştı. Özel durumları elde etmek için genel formülün nasıl kullanılacağına dair tam bir resim elde etmek adına burada ilgili açıklamaları sunacağım. Fraktal, atom bombasında olduğu gibi zincirleme reaksiyon prensibine göre çalışan bir fonksiyondur. Ayarlanan zincirleme reaksiyon çok derinse, bilgisayar bu kadar büyük hesaplamalarla başa çıkamayabilir. Eğer durum özellikle kritik değilse, dakikalar, saatler ve hatta günler gibi çok uzun bir süre hesaplama yapılacaktır.
Yazar: Evgeniy Ilin