"Üçüncü Nesil Nöral Ağlar: Derin Ağlar" makalesi için tartışma

Yury Reshetov 2014.11.27 14:01 #11

vlad1949:

Bu benim için bir soru değil. Makale hakkında söyleyeceklerin bu kadar mı?

Makaleye ne olmuş? Tipik bir yeniden yazma. Diğer kaynaklarda da aynı şeyler var, sadece biraz farklı kelimelerle. Resimler bile aynı. Yeni bir şey görmedim, yani yazara ait.

Örnekleri denemek istedim ama bu çok kötü oldu. Bölüm MQL5 için ama örnekler MQL4 için.

Geleceğe bakmanın bir yolu Hatalar, hatalar, sorular Ticarette makine öğrenimi: teori,

СанСаныч Фоменко 2014.11.27 14:18 #12

vlad1949

Sevgili Vlad!

Arşivlere baktım, oldukça eski R belgelerine sahipsiniz. Ekteki kopyalarla değiştirmek iyi olacaktır.

Dosyalar:

Doc_R.zip 2181 kb

СанСаныч Фоменко 2014.11.27 14:26 #13

vlad1949

Sevgili Vlad!

Test cihazında neden çalıştıramadınız?

Her şey sorunsuz çalışıyor. Ancak şema bir gösterge olmadan: Uzman Danışman doğrudan R ile iletişim kurar.

Vladimir 2014.11.27 16:56 #14

Jeffrey Hinton, derin ağların mucidi: "Derin ağlar yalnızca sinyal-gürültü oranının yüksek olduğu verilere uygulanabilir. Finansal seriler o kadar gürültülü ki derin ağlar uygulanamaz. Denedik ama başarılı olamadık."

YouTube'daki derslerini dinleyin.

Hatalar, hatalar, sorular STOK haberleri , tahminler "Rastgele Ormanlar Öngörü Trendleri"

СанСаныч Фоменко 2014.11.27 17:01 #15

gpwr:

Jeffrey Hinton, derin ağların mucidi: "Derin ağlar yalnızca sinyal-gürültü oranının yüksek olduğu verilere uygulanabilir. Finansal seriler o kadar gürültülü ki derin ağlar uygulanamaz. Denedik ama başarılı olamadık."

Youtube'daki derslerini dinleyin.

Paralel başlıktaki gönderinizi göz önünde bulundurarak.

Gürültü, sınıflandırma görevlerinde radyo mühendisliğinden farklı anlaşılır. Bir tahmin edici, hedef değişken için zayıf bir şekilde ilişkiliyse (zayıf tahmin gücüne sahipse) gürültülü olarak kabul edilir. Tamamen farklı bir anlam. Hedef değişkenin farklı sınıfları için tahmin gücüne sahip tahmin ediciler aranmalıdır.

Ticarette makine öğrenimi: teori, "Sinir Ağları Ucuz ve "Rastgele Ormanlar Öngörü Trendleri"

Vladimir 2014.11.27 17:14 #16

Ben de benzer bir gürültü anlayışına sahibim. Finansal seriler, çoğu bizim tarafımızdan bilinmeyen ve seriye bu "gürültüyü" katan çok sayıda tahmin ediciye bağlıdır. Sadece kamuya açık tahmin edicileri kullanarak, hangi ağları veya yöntemleri kullanırsak kullanalım hedef değişkeni tahmin edemeyiz.

Nöro ağlar MT5 için dilekler Ticarette makine öğrenimi: teori,

СанСаныч Фоменко 2014.11.27 17:24 #17

gpwr:
Ben de benzer bir gürültü anlayışına sahibim. Finansal seriler, çoğu bizim tarafımızdan bilinmeyen ve seriye bu "gürültüyü" katan çok sayıda tahmin ediciye bağlıdır. Sadece kamuya açık tahmin edicileri kullanarak, hangi ağları veya yöntemleri kullanırsak kullanalım hedef değişkeni tahmin edemeyiz.

Başlığıma bakınız.

Vladimir Perervenko 2014.11.28 07:38 #18

faa1947:

vlad1949

Sevgili Vlad!

Test cihazında neden çalıştıramadınız?

Her şey sorunsuz çalışıyor. Gösterge olmadan doğru şema: danışman doğrudan R ile iletişim kurar.

llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll

İyi günler SanSanych.

Yani ana fikir, birkaç gösterge ile çoklu para birimi yapmaktır.

Aksi takdirde, elbette, her şeyi bir Uzman Danışmana paketleyebilirsiniz.

Ancak eğitim, test ve optimizasyon, ticareti kesintiye uğratmadan anında uygulanacaksa, tek Uzman Danışmanlı varyantın uygulanması biraz daha zor olacaktır.

İyi şanslar

PS. Testin sonucu nedir?

Vladimir Perervenko 2014.11.28 07:44 #19

Selamlar SanSanych.

Burada İngilizce konuşulan bir forumda bulduğum optimum küme sayısını belirlemeye yönelik bazı örnekler var. Hepsini kendi verilerimde kullanamadım. Çok ilginç 11 paket "clusterSim".

--------------------------------------------------------------------------------------

#
n = 100
g = 6 
set.seed(g)
d <- data.frame(x = unlist(lapply(1:g, function(i) rnorm(n/g, runif(1)*i^2))), 
                y = unlist(lapply(1:g, function(i) rnorm(n/g, runif(1)*i^2))))
plot(d)
--------------------------------------
#1 
library(fpc)
pamk.best <- pamk(d)
cat("number of clusters estimated by optimum average silhouette width:", strpamk.best$nc, "\n")
plot(pam(d, pamk.best$nc))

#2 we could also do:
library(fpc)
asw <- numeric(20)
for (k in 2:20)
  asw[[k]] <- pam(d, k) $ silinfo $ avg.width
k.best <- which.max(asw)
cat("silhouette-optimal number of clusters:", k.best, "\n")
---------------------------------------------------
#3. Calinsky criterion: Another approach to diagnosing how many clusters suit the data. In this case 
# we try 1 to 10 groups.
require(vegan)
fit <- cascadeKM(scale(d, center = TRUE,  scale = TRUE), 1, 10, iter = 1000)
plot(fit, sortg = TRUE, grpmts.plot = TRUE)
calinski.best <- as.numeric(which.max(fit$results[2,]))
cat("Calinski criterion optimal number of clusters:", calinski.best, "\n")
# 5 clusters!
-------------------
4. Determine the optimal model and number of clusters according to the Bayesian Information 
Criterion for expectation-maximization, initialized by hierarchical clustering for parameterized 
Gaussian mixture models
library(mclust)
# Run the function to see how many clusters
# it finds to be optimal, set it to search for
# at least 1 model and up 20.
d_clust <- Mclust(as.matrix(d), G=1:20)
m.best <- dim(d_clust$z)[2]
cat("model-based optimal number of clusters:", m.best, "\n")
# 4 clusters
plot(d_clust)
----------------------------------------------------------------
5. Affinity propagation (AP) clustering, see http://dx.doi.org/10.1126/science.1136800 
library(apcluster)
d.apclus <- apcluster(negDistMat(r=2), d)
cat("affinity propogation optimal number of clusters:", length(d.apclus@clusters), "\n")
# 4
heatmap(d.apclus)
plot(d.apclus, d)
---------------------------------------------------------------------
6. Gap Statistic for Estimating the Number of Clusters. 
See also some code for a nice graphical 
output . Trying 2-10 clusters here:
library(cluster)
clusGap(d, kmeans, 10, B = 100, verbose = interactive())
-----------------------------------------------------------------------
7. You may also find it useful to explore your data with clustergrams to visualize cluster 
assignment, see http://www.r-statistics.com/2010/06/clustergram-visualization-and-diagnostics-for-cluster-analysis-r-code/&nbsp; 
for more details.
-------------------------------------------------------------------
#8. The NbClust package  provides 30 indices to determine the number of clusters in a dataset.
library(NbClust)
nb <- NbClust(d, diss = NULL, distance = "euclidean", 
        min.nc=2, max.nc=15, method = "kmeans", 
        index = "alllong", alphaBeale = 0.1)
hist(nb$Best.nc[1,], breaks = max(na.omit(nb$Best.nc[1,])))
# Looks like 3 is the most frequently determined number of clusters
# and curiously, four clusters is not in the output at all!
-----------------------------------------
Here are a few examples:
d_dist <- dist(as.matrix(d))   # find distance matrix 
plot(hclust(d_dist))           # apply hirarchical clustering and plot
----------------------------------------------------
#9 Bayesian clustering method, good for high-dimension data, more details:
# http://vahid.probstat.ca/paper/2012-bclust.pdf
install.packages("bclust")
library(bclust)
x <- as.matrix(d)
d.bclus <- bclust(x, transformed.par = c(0, -50, log(16), 0, 0, 0))
viplot(imp(d.bclus)$var); 
plot(d.bclus); 
ditplot(d.bclus)
dptplot(d.bclus, scale = 20, horizbar.plot = TRUE,varimp = imp(d.bclus)$var, horizbar.distance = 0, dendrogram.lwd = 2)
-------------------------------------------------------------------------
#10 Also for high-dimension data is the pvclust library which calculates 
#p-values for hierarchical clustering via multiscale bootstrap resampling. Here's #the example from the documentation (wont work on such low dimensional data as in #my example):
library(pvclust)
library(MASS)
data(Boston)
boston.pv <- pvclust(Boston)
plot(boston.pv)
------------------------------------
###Automatically cut the dendrogram
require(dynamicTreeCut)
ct_issues <- cutreeHybrid(hc_issues, inverse_cc_combined, minClusterSize=5)
-----
FANNY <- fanny(as.dist(inverse_cc_combined),, k = 3, maxit = 2000) 
FANNY$membership MDS <- smacofSym(distMat)$conf 
plot(MDS, type = "n") text(MDS, label = rownames(MDS), col = rgb((FANNY$membership)^(1/1)))
-----
m7 <- stepFlexmix
----------------------
#11 "clusterSim" -Department of Econometrics and Computer Science, University of #Economics, Wroclaw, Poland
http://keii.ue.wroc.pl/clusterSim
See file ../doc/clusterSim_details.pdf for further details
data.Normalization Types of variable (column) and object (row) normalization formulas
Description
Types of variable (column) and object (row) normalization formulas
Usage
data.Normalization (x,type="n0",normalization="column")
Arguments
x vector, matrix or dataset
type type of normalization: n0 - without normalization
n1 - standardization ((x-mean)/sd)
n2 - positional standardization ((x-median)/mad)
n3 - unitization ((x-mean)/range)
n3a - positional unitization ((x-median)/range)
n4 - unitization with zero minimum ((x-min)/range)
n5 - normalization in range <-1,1> ((x-mean)/max(abs(x-mean)))
n5a - positional normalization in range <-1,1> ((x-median)/max(abs(x-median)))
n6 - quotient transformation (x/sd)
n6a - positional quotient transformation (x/mad)
n7 - quotient transformation (x/range)
n8 - quotient transformation (x/max)
n9 - quotient transformation (x/mean)
n9a - positional quotient transformation (x/median)
n10 - quotient transformation (x/sum)
n11 - quotient transformation (x/sqrt(SSQ))
normalization "column" - normalization by variable, "row" - normalization by objec
See file ../doc/HINoVMod_details.pdf for further details

Bir sonraki yazıda verilerimle hesaplamalar

İlginç ve Mizah "OpenCL: Paralel dünyalara köprü" MT5 platformunu kitlelere tanıtmak

Vladimir Perervenko 2014.11.28 08:10 #20

Optimum küme sayısı çeşitli paketlerle ve 30'dan fazla optimallik kriteri kullanılarak belirlenebilir. Gözlemlerime göre en çok kullanılan kriter Calinskykriteridir .

Setimizdeki ham verileri dt göstergesinden alalım . 17 tahminci, hedef y ve mum çubuğu gövdesi z içerir.

"magrittr" ve "dplyr" paketlerinin son sürümlerinde birçok yeni güzel özellik var, bunlardan biri de 'pipe' - %>%. Ara sonuçları kaydetmeniz gerekmediğinde çok kullanışlıdır. Kümeleme için ilk verileri hazırlayalım. Başlangıç matrisi dt'yi alın, ondan son 1000 satırı seçin ve sonra onlardan değişkenlerimizin 17 sütununu seçin. Daha net bir gösterim elde ederiz, başka bir şey değil.

> library(magrittr)
> x<-dt %>% tail( .,1000)%>% extract( ,1:17)

1.

> library(fpc)
> pamk.best <- pamk(x)
> cat("number of clusters estimated by optimum average silhouette width:", pamk.best$nc, "\n")
> number of clusters estimated by optimum average silhouette width: h: 2

2. Calinsky kriteri: Verilere kaç kümenin uygun olduğunu teşhis etmek için başka bir yaklaşım. Bu durumda

1 ila 10 grup deniyoruz.

> require(vegan)
> fit <- cascadeKM(scale(x, center = TRUE,  scale = TRUE), 1, 10, iter = 1000)
> plot(fit, sortg = TRUE, grpmts.plot = TRUE)

> calinski.best <- as.numeric(which.max(fit$results[2,]))
> cat("Calinski criterion optimal number of clusters:", calinski.best, "\n")
Calinski criterion optimal number of clusters: 2

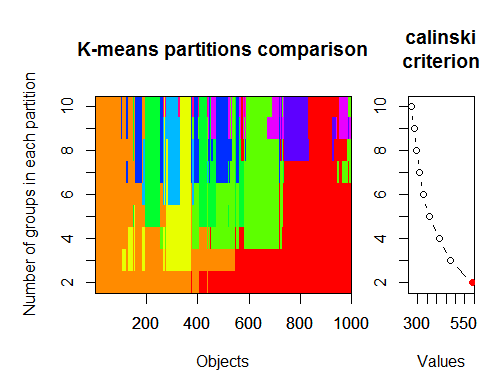
3. Parametrelendirilmiş Gauss karışım modelleri için hiyerarşik kümeleme ile başlatılan beklenti maksimizasyonu için Bayesian Bilgi Kriterine göre en uygun modeli ve küme sayısını belirleyin.

Gauss karışım modelleri

> library(mclust)
#  Run the function to see how many clusters
#  it finds to be optimal, set it to search for
#  at least 1 model and up 20.
> d_clust <- Mclust(as.matrix(x), G=1:20)
> m.best <- dim(d_clust$z)[2]
> cat("model-based optimal number of clusters:", m.best, "\n")
model-based optimal number of clusters: 7

Ticarette makine öğrenimi: teori, Mql5 dilinin özellikleri, incelikleri Elit göstergeler :)

"Üçüncü Nesil Nöral Ağlar: Derin Ağlar" makalesi için tartışma - sayfa 2