Обсуждение статьи "Статистические распределения в MQL5 - берем лучшее из R и делаем быстрее" - страница 19

[Aleksey Nikolayev]

Aleksey Nikolayev:
Есть пожелание, чтобы в библиотеку было добавлено распределение Колмогорова. Оно весьма полезно из-за использования в критерии Колмогорова-Смирнова и в задаче поиска разладки случайного процесса.

На всякий случай оставлю здесь. Вычисление CDF и дополнения к ней для распределения статистики Колмогорова-Смирнова для двустороннего одновыборочного теста.

[Aleksey Nikolayev]

Кто-нибудь пользовался этим?

[Renat Fatkhullin]

Aleksey Nikolayev:

Некорректно вычисляется CDF гипергеометрического распределения функцией MathCumulativeDistributionHypergeometric(). По определению, функция распределения вероятностей должна быть определена для любого действительного числа. Ниже скрипт на mql5 с результатами его работы и, для сравнения, то же самое на R.

результат:

-1.0 nan 2

0.0 0.0 0

0.5 nan 2

zero divide in 'Hypergeometric.mqh' (241,35)

результат:

[1] 0.0000000 0.0000000 0.0000000 0.2222222

Вы передали неверные аргументы и получили ERR_ARGUMENTS_INVALID (2). Мы более детально проверяем входные параметры, а R судя по всему ответ заменил на нули.

//+------------------------------------------------------------------+
//| Hypergeometric cumulative distribution function (CDF)            |
//+------------------------------------------------------------------+
//| The function returns the probability that an observation         |
//| from the Hypergeometric distribution with parameters m,n,k       |
//| is less than or equal to x.                                      |
//|                                                                  |
//| Arguments:                                                       |
//| x          : The desired number of objects                       |
//| m          : Size of the population                              |
//| k          : Number of items with the desired characteristic     |
//|              in the population                                   |
//| n          : Number of samples drawn                             |
//| tail       : Flag to calculate lower tail                        |
//| log_mode   : Logarithm mode,if true it calculates Log values     |
//| error_code : Variable for error code                             |
//|                                                                  |
//| Return value:                                                    |
//| The value of the Hypergeometric cumulative distribution function |
//| with parameters m,n,k, evaluated at x.                           |
//+------------------------------------------------------------------+
//| Based on algorithm by John Burkardt                              |
//+------------------------------------------------------------------+
double MathCumulativeDistributionHypergeometric(const double x,const double m,const double k,const double n,const bool tail,const bool log_mode,int &error_code)
  {
//--- check NaN
   if(!MathIsValidNumber(x) || !MathIsValidNumber(m) || !MathIsValidNumber(k) || !MathIsValidNumber(n))
     {
      error_code=ERR_ARGUMENTS_NAN;
      return QNaN;
     }
//--- m,k,n,x must be integer
   if(m!=MathRound(m) || k!=MathRound(k) || n!=MathRound(n) || x!=MathRound(x))
     {
      error_code=ERR_ARGUMENTS_INVALID;
      return QNaN;
     }
//--- m,k,n,x must be positive
   if(m<0 || k<0 || n<0 || x<0)
     {
      error_code=ERR_ARGUMENTS_INVALID;
      return QNaN;
     }
//--- check ranges
   if(n>m || k>m)
     {
      error_code=ERR_ARGUMENTS_INVALID;
      return QNaN;
     }

[Renat Fatkhullin]

Aleksey Nikolayev:

Отрицательны некоторые (не все) биномиальные коэффициенты, например:

результат:     -309196571788882235

должно быть: 349615716557887488

Из-за большого K (28) там банально 64 битный long переполнился. Возвратное значение - long.

Чтобы считать значения в таких пределах, надо переписать функцию на double значения.

[Aleksey Nikolayev]

Renat Fatkhullin:

Вы передали неверные аргументы и получили ERR_ARGUMENTS_INVALID (2). Мы более детально проверяем входные параметры, а R судя по всему ответ заменил на нули.

1) Любая CDF - функция распределения вероятностей (дискретные - не исключение!) ПО ОПРЕДЕЛЕНИЮ должна быть определена для всех вещественных чисел. Ниже приведён аналог кода на R с его результатом, показывающий как это должно считаться в действительности. Кстати, некоторые дискретные CDF функции у вас считают правильно, а некоторые - нет.

2) Для значения 1 выдаётся ошибка деления на ноль.

[Renat Fatkhullin]

Aleksey Nikolayev:

1) Любая CDF - функция распределения вероятностей (дискретные - не исключение!) ПО ОПРЕДЕЛЕНИЮ должна быть определена для всех вещественных чисел. Ниже приведён аналог кода на R с его результатом, показывающий как это должно считаться в действительности. Кстати, некоторые дискретные CDF функции у вас считают правильно, а некоторые - нет.

2) Для значения 1 выдаётся ошибка деления на ноль.

Почитайте код функции и ее проверки, она в исходниках.

Под рукой нет R, надо отдельно проверять. Деление на ноль вижу, нужно разбираться в пограничных условиях.

[Aleksey Nikolayev]

Renat Fatkhullin:

Из-за большого K (28) там банально 64 битный long переполнился. Возвратное значение - long.

Чтобы считать значения в таких пределах, надо переписать функцию на double значения.

Это понятно. Просто ещё есть ошибка с логарифмом биномиального коэффициента при целых аргументах и я решил, что это и есть причина. Сейчас посмотрел код и понял, что ошибался - причина в чём-то другом.

#include <Math\Stat\Math.mqh>

void OnStart()
  { Print(MathBinomialCoefficientLog(62,28));
    Print(MathBinomialCoefficientLog(62.0,28.0));
  }

результат:

test_clog (EURUSD.m,MN1) -nan(ind)

test_clog (EURUSD.m,MN1) 40.39561099351077

PS Ошибся, проблема тоже в переполнении

[Aleksey Nikolayev]

Renat Fatkhullin:

Под рукой нет R,

R онлайн

[Denis Kirichenko]

Какая-то беда с NoncentralBeta. Взял скрипт из Документации.

Вот такие результаты для разных параметров.

[Denis Kirichenko]

Формула в Документации:

это аналог в Википедии:

Посмотрел код.

В функции MathRandomNoncentralBeta() есть такие строки:

//--- generate random number using Noncentral ChiSquare
double chi1=MathRandomNoncentralChiSquare(a2,lambda2,error_code);
double chi2=MathRandomNoncentralChiSquare(b2,lambda2,error_code);
result[i]=chi1/(chi1+chi2);

В той же Википедии есть такое:

The noncentral beta distribution (Type I) is the distribution of the ratio

 

where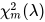   is a noncentral chi-squared random variable with degrees of freedom m and noncentrality parameter  𝜆 , and  𝜒 𝑛 2  is a central chi-squared random variable with degrees of freedom n, independent of  𝜒 𝑚 2 ( 𝜆 ) .

Т.е. берутся две случайные величины, где первая из нецентрального хи-квадрат распределения, а вторая - из центрального. Наверное код можно исправить на такой:

//--- generate random number using Noncentral ChiSquare
double chi1=MathRandomNoncentralChiSquare(a2,lambda2,error_code);
double chi2=MathRandomChiSquare(b2,error_code);
result[i]=chi1/(chi1+chi2);

Изменённые графики в примере будут ниже.