Линия тренда по трем фракталам

Iurii Tokman 2020.04.11 17:30 #1

последний фрактал будет с погрешностью, плюс минус по цене
редкость если он будет именно на линии

Nikolai Semko 2020.04.12 06:57 #2

ualexxx:

Всем привет!
Скажите, пожалуйста, есть ли возможность "научить" данный индикатор (или какой-то другой) строить прямые трендовые линии по трем(!) последним фракталам и, при появлении таковой, трезвонить об этом алертами и срелять пушами (такая-то пара, на таком-то тайме появилась линия)? как указанно на рисунке:

Я понимаю, о чем Вы, но это не очень эффективно. Линии будут "прыгать", в них не будет постоянства. Это очевидно из этой гифки по вашему индикатору:

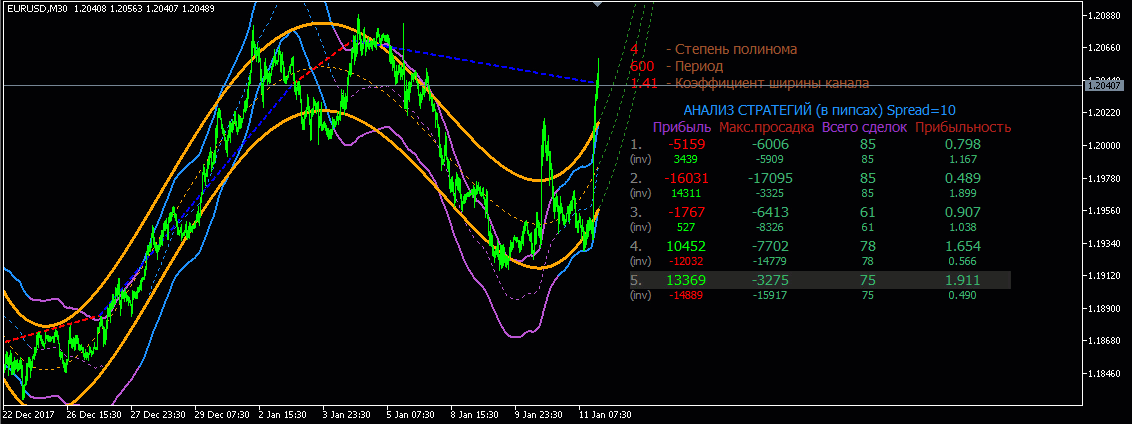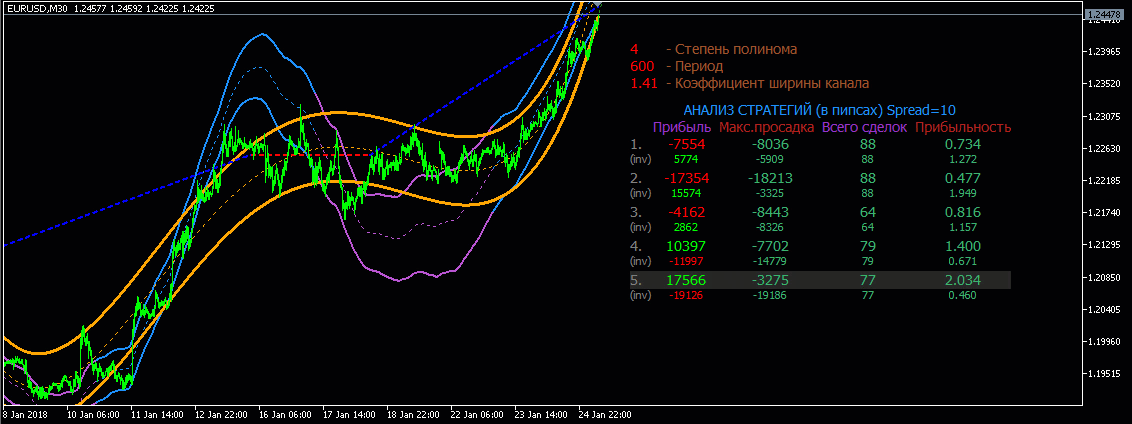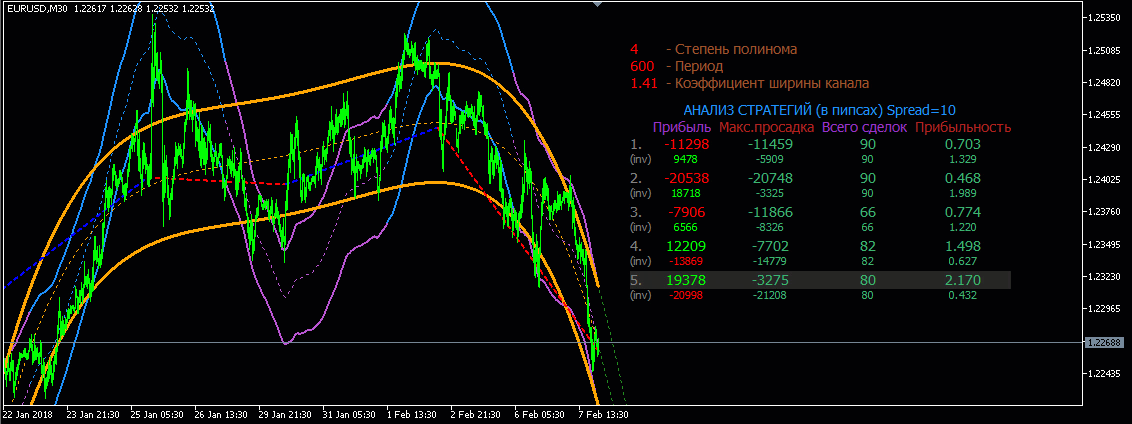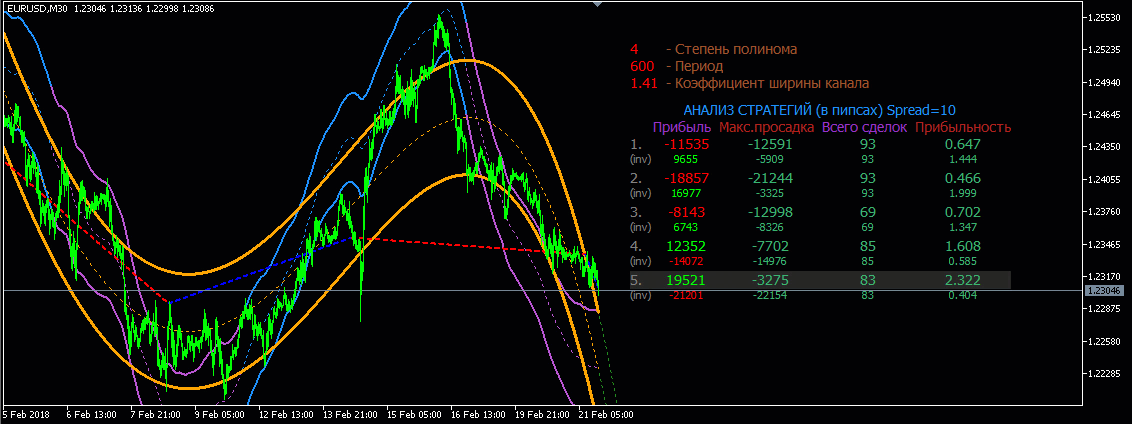
Гораздо больше толку строить экстраполяцию от полиномиальной апроксимации различный степеней.
Для наглядности что-то типа такого:

Индикаторы форекс От теории к практике. Сервисдеск. Жалобы, предложения.

Nikolai Semko 2020.04.12 22:02 #3

ualexxx:

Всем привет!
Скажите, пожалуйста, есть ли возможность "научить" данный индикатор (или какой-то другой) строить прямые трендовые линии по трем(!) последним фракталам и, при появлении таковой, трезвонить об этом алертами и срелять пушами (такая-то пара, на таком-то тайме появилась линия)? как указанно на рисунке:

но если очень хочется, то зачем строить прямые линии. Через любые три точки проходит только одна парабола. Парабола более информативней, чем прямая.
формула параболы:

Price = a+b*n+c*n²
где a, b, c - коэффициенты, n - номер бара.

нужно будет решить систему из трех уравнений. Математика очень простая.
Можете здесь подсмотреть (функция ABC)

Можно строить также и по 4 точкам, но не параболу, а полином 3-й степени (будет система уравнений из 4 уравнений 3й степени) и т.д.
Но еще более эффективно строить параболический канал по 4 точкам (2 нижних экстремума и 2 верхних экстремума). Через такую комбинацию проходит только один равноудаленный параболический канал. В этом случае кроме коэффициентов a,b,c нужно будет найти ширину канала h. Математика тоже очень простая из средней школы(система уравнений из 4х квадратных уравнений).

6-я степень Поли Помогите! Выявления диагонали движущего объекта Любые вопросы новичков по

Алексей Тарабанов 2020.04.13 02:19 #4

Полином любой степени:

Private Function Lagrange(t, n, m, i As Integer) As Double
    Dim j, k As Integer
    Dim l As Double
    Lagrange = 0  ' Экстраполяция значения в точке t>n по значениям в точках 0...n
    For j = 0 To n
        l = 1
        For k = 0 To n
            If k <> j Then l = l * (t - k) / (j - k) ' Форма Лагранжа
        Next k
        Lagrange = Lagrange + l * Cells(m + j, i)    ' Получать значения в точках из диапазона ячеек (m,i):(m+n,i)
    Next j
End Function

Только, неблагодарное это занятие. Чем выше степень полинома, тем более он "дёрганный".

Вообще, применение интерполяционных методов (Фурье, Лагранж, Тейлор) для решения экстраполяционных задач - тупик, имхенько.

Гифки красивые )

Renat Akhtyamov 2020.04.13 05:46 #5

Nikolai Semko:

Я понимаю, о чем Вы, но это не очень эффективно. Линии будут "прыгать", в них не будет постоянства. Это очевидно из этой гифки по вашему индикатору:

Гораздо больше толку строить экстраполяцию от полиномиальной апроксимации различный степеней.
Для наглядности что-то типа такого:

особенно понравилось наличие теста стратегий и графическое изображения открытой сделки

а вот на первой картинке почему то трендовая по 2-м фракталам, а не по трем

Nikolai Semko 2020.04.13 13:14 #6

Renat Akhtyamov:

а вот на первой картинке почему то трендовая по 2-м фракталам, а не по трем

потому что у хозяина ветки так было реализовано.