Добрый день.. Я сделал новую систему.. в ней нет еще пока стопов..торгует по сигналу и выходит по этому же сигналу.. Как вы думаете какой наилучший алгоритм Money Management в нее поставить?
http://i.imgur.com/Tgkw1.gif
попробуй формулу Келли.
попробуй формулу Келли.
Келли работает для взяток фиксированной величины, а у товарища самый общий случай. Для него нужно честно брать интеграл от распределения взяток и максимизировать его.
Пусть топикстартер выложит плотность распределения взяток для своей ТС и я выдам на-гора заточенный оптимум для лота как функцию от величины депозита.
Добрый день.. Я сделал новую систему.. в ней нет еще пока стопов..торгует по сигналу и выходит по этому же сигналу.. Как вы думаете какой наилучший алгоритм Money Management в нее поставить?
http://i.imgur.com/Tgkw1.gif
Такую систему, с ПФ=1 спасет только мартингейл :)) да и то... 7 непрерывно убыточных сделок для мартина многовато ;)
Такую систему, с ПФ=1 спасет только мартингейл :)) да и то... 7 непрерывно убыточных сделок для мартина многовато ;)
Europa: Профит фактор это Прибыль/убыток... в этой системе сейчас нет стопов, и поэтому были трейды где она проигрывала за раз больше 10% от всего капитала.. Поэтому Я попросил какой алгоритм ММ ей задать чтобы уменьшить Убыток и повысить прибыл (ПФ возрастет естественно). Neutron, буду очень признателен если выложишь заточенный оптимум для нее и покажешь как это считается...
Пусть топикстартер выложит плотность распределения взяток для своей ТС и я выдам на-гора заточенный оптимум для лота как функцию от величины депозита.
Сергей, было бы интересно взглянуть на метод расчета оптимума.
Может что и пойму.
Только речь идет о методе, а не о самом расчете
Хотя сам расчет позволит лучше понять метод
Это конечно если метод не Ноу-Хау
Келли работает для взяток фиксированной величины, а у товарища самый общий случай. Для него нужно честно брать интеграл от распределения взяток и максимизировать его.
Пусть топикстартер выложит плотность распределения взяток для своей ТС и я выдам на-гора заточенный оптимум для лота как функцию от величины депозита.
Только недавно начал юзать Метатредйдер... Где я беру плотность распределения взяток ТС? Я выложил стату что выдал мне Метатрейдер.. или это все взятки что были в "Результаты"?
Сергей, было бы интересно взглянуть на метод расчета оптимума.
Привет, Виктор.
У меня есть наработанный материал по теме.
Начнём с алгоритмизации работы самой простой произвольной ТС с реинвестированием капитала f. Напомню, что в нашем случае доля капитала f определяется как относительная и безразмерная величина средств приходящаяся на один пункт движения цены. Пусть в начальный момент времени мы имели капитал K[0] и в результате первой транзакции мы заработали (проиграли) у рынка h[1] пунктов, где h может принимать любые натуральные значения, т.е. h может быть равной 5 пунктов (и мы выиграли эту взятку) или -51 пункт и мы проиграли (вернули рынку) 51 пункт. Тогда, денежный прирост нашего капитала в результате первой сделки будет определятся величиной K[1]=K[0]+h[1]*f*K[0], это может быть как прирост, так и убыль капитала, всё определяется знаком перед h[1] и его абсолютной величиной. Для второй транзакции выражение выглядит аналогично уже написанному: K[2]=K[1]+h[2]*f*K[1]. Напомню, что доля капитала f участвующего в торгах фиксирована. В общем виде, через i проведённых транзакций размер нашего депозита будет определятся величиной K[i]= K[i-1]* (1+h[i]*f), учитывая, что мы шагом ранее уже получили выражение для величины K[i-1], мы можем подставить его в последнюю формулу и получим: K[i]= K[i-2]* (1+h[i-1]*f)* (1+h[i]*f). Продолжая далее по цепочке получаем:
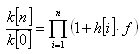
Мы получили выражение, которое показывает относительную величину приращения нашего депозита K[n] к его стартовой величине K[0] через n транзакций для произвольной ТС, которая определена через величины своих взяток h[i]. Символ П обозначает произведение скобок друг на друга. Пока всё. Дело в том, что продвижение дальше с выражением для роста депозита представленного в такой форме невозможно. Но мы проделаем хитрый финт ушами, а именно, вспомним тот факт, что значения, которые могут принимать наши пунктовые взятки h[i] - являются целыми числами и при большом числе транзакций всегда можно выделить группы взяток с одинаковым числом пунктов в каждой взятке. Таким образом, перегруппируем члены в произведении в "произведение кучек" по интересам и воспользуемся тем фактом, что от перестановки мест членов в произведении, произведение не меняется.
Тогда выражение можно представить в виде:
мы смогли перейти от сплошного произведения к произведению групп с одинаковым параметром h[j]. Эти группы уже можно заменить на простенькие выражения с показателем степени g[j] равным числу элементов в данной группе (см. правую часть выражения для прироста депозита).
Необходимо исследовать полученное выражение на экстремум, который максимизирует прирост депозита за единицу времени как функцию параметра f. Для этого упростим полученное выражение, воспользовавшись тем фактом, что экстремум гладкой функции (а именно он нас интересует) не сместится, если посмотреть на "вазу" через увеличилку (образно). В нашем случае, в качестве увеличилки мы используем логарифмическую функцию. Её прелесть в том, что она монотонна и переводит произведение величин в их сумму (не смещая экстремум):
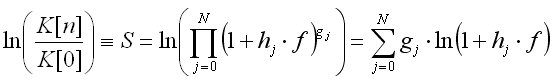
Будем далее для простоты обозначать логарифм прибыли через S и заметим, что g[j] есть не что иное как функция распределения (ФР) числа (количества) взяток такого-то размера (аргумент). Вот к примеру, как выглядит ФР наугад взятой ТС:
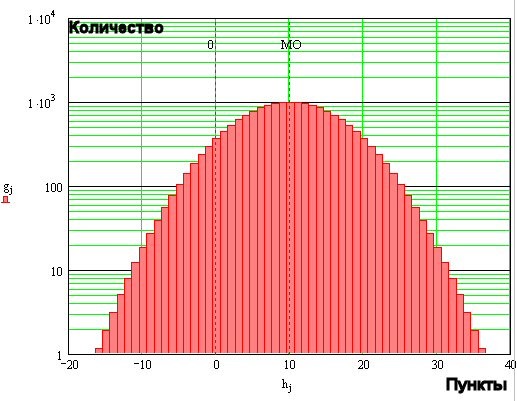
Видно, что взятки могут быть как проигрышные, так и выигрышные (положительные). Так же можно обратить внимание на то, что взяток с небольшим размахом заметно больше, чем с большим и т.д. Не составляет труда найти МО для такой ТС:
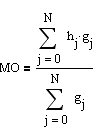
Видно, что МО=10 пунктам и данная абстрактная ТС смогла бы приносить профит для инструментов с комиссией меньше 10 пунктов. Пока оставляем за бортом все вопросы связанные с эргодичностью и т.п. т.к. рассматриваем иллюстрацию предложенного подхода.
Так вот, всё это служит подготовкой тому, что для поиска оптимальной доли депозита f, необходимо знать закон распределения числа взяток для конкретной ТС (и желательно, в аналитическом виде). Зная его, мы подставляем полученное выражение для ФР в формулу для логарифма прибыли и ищем его максимум. Например, для данного случая закон распределения взяток имеет гауссов вид и не составляет труда записать его в аналитическом виде:
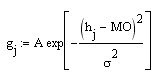
Или для логарифма прибыли:
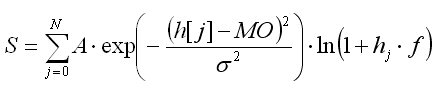
Можно проделать второй финт ушами и перейти от суммы к интегралу. Для этого достаточно поделить и умножить полученную сумму на одно и то же число, которое мы примем равным одному пункту (проще говоря - единице) или, что то же самое - шагу дескретизации dh по оси абсцисс:
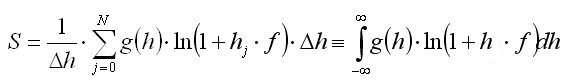
Я умышлено перешёл к бесконечным пределам интегрирования т.к. ФР взяток у нас не ограничена и взятки для самой общей ТС могут принимать любые значения (в данном случае h определена на всей области действительных чисел, что не соответствует реальности, но это не принципиально и не влияет на полученный результат, зато позволяет перейти от сумм к интегралам - они иногда берутся). 1/dh перед интегралом опущена т.к. тождественно равна единице.
Из последнего выражения, как частный случай, получается формула Келли. Для него функция рвспределения g(x) это два дискретных значения и интеграл сводится к сумме двух чисел. Дальше ищем максимум по параметру f - доли депозита и получаем оптимальный ММ. Для общего случая, как у топикстартера, нужно построить распределение взяток по амплитуде (с учётом спреда) и брать полученный интеграл (или сумму).
Говоря о практической применимости полученного для оптимального ММ выражения, необходимо иметь навыки работы с матпакетами. Не думаю, что можно получить аналитическое выражение для произвольной ТС. Самый простой случай с фиксированными взятками решается в лёт и даёт зависимость оптимальной доли депозита как функцию величины депозита, отношения проигрышных сделок к выигрышным и их величин. Если есть возможность получить (не в тестере МТ) вид распределения взяток g(h), то можно записать общий вид выражения для оптимального ММ с уётом спреда, и величин стопордеров. Что даст возможность извлечь оптимальные значения StopLoss и TakeProfit для конкретной ТС.
Есть другой вариант расчета, я его просчитывал вручную, но пока не довел до автоматизации. Работает примерно так.
Мы ставим задачу для некоторой ТС по возможности максимизировать средний результат сделки в пунктах, применяя для этого по возможности простой метод расчета (сразу оговорюсь, что точный максимум мы в любом случае не получим, т.к. не имеем возможности учесть абсолютно все факторы работы ТС). Для этого поступим следующим образом.
Зададимся некоторой глубиной анализа результатов предыдущих сделок - 2,3,4 или больше, в зависимости от того, каким объемом сделок для анализа мы располагаем. В общем случае, если мы хотим анализировать глубину в n сделок, нам будет необходимо собирать статистику для 2^n вариантов, при этом даже самый редкий из них должен встретиться в истории торговли хотя бы с десяток раз, чтобы иметь возможность сколь-нибудь доверять результату. Анализировать будем бинарный результат n предыдущих сделок (1 - прибыль, 0 - убыток), получая таким образом для каждой последовательности из нулей и единиц матожидание прибыли (для определенности - в единицах валюты в расчете на сделку в 1 лот) для сделки, следующей за данной последовательностью.
Далее мы делаем предположение, что данное распределение более-менее постоянно на всей генеральной совокупности сделок (по сути, без этого предположения нет вообще смысла в каком-либо ММ).
Итак, мы получили эмпирическую таблицу распределения прибыльности торговли в зависимости от результатов предыдущих сделок {K(Xi)}. Кроме того, нам необходимо подсчитать частоту встречаемости каждой комбинации в отдельности {P(Xi)}. Теперь можно переходить к формализации задачи. Мы хотим подобрать для каждой комбинации результатов предыдущих сделок такой размер лота (т.е. вектор {L[i]}), при котором средняя прибыль будет максимальна при условии постоянного среднего лота (например, равного 1). Соответствующая система условий будет выглядеть следующим образом:
Необходимо найти вектор {L[i]}, такой, что
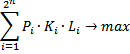
при условиях
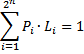
и
![]() .
.
(первое условие - постоянство среднего лота; второе означает наше "доверие" нашей стратегии торговли, т.е. мы не хотим переворачивать сделки ни при каких условиях - в принципе это условие можно и отменить, тогда значение компоненты вектора со знаком минус будет означать необходимость входа в направлении, обратном рекомендуемому торговой системой)
Т.о. имеем стандартную задачу линейного программирования, которая решается стандартным же симплекс-методом.
to Alsu
Первый раз прочитал. Захожу на второй круг...
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования

Добрый день.. Я сделал новую систему.. в ней нет еще пока стопов..торгует по сигналу и выходит по этому же сигналу.. Как вы думаете какой наилучший алгоритм Money Management в нее поставить?
http://i.imgur.com/Tgkw1.gif