Discussão do artigo "Algoritmos de otimização populacionais: otimização de dinâmica espiral (Spiral Dynamics Optimization, SDO)"
Gostaria de consultar a comunidade.
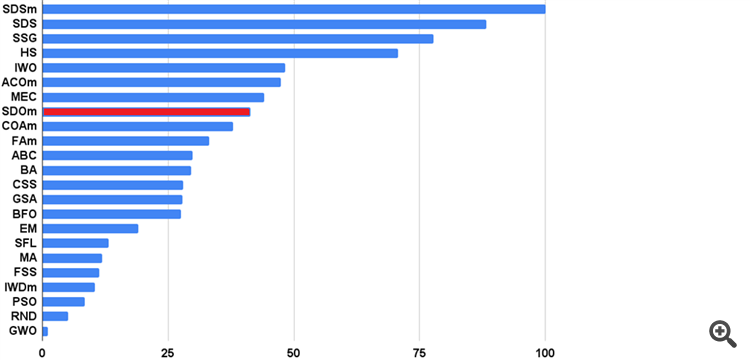
Outros algoritmos incríveis estão aguardando sua vez, a tabela de comparação se torna muito grande para uma visualização e análise convenientes, penso em excluir os mais fracos da tabela, mas, por outro lado, não gostaria de perdê-los de vista.
Além disso, talvez eu possa fazer alguma outra visualização.
Em geral, ficarei feliz em ouvir seus comentários e sugestões.
Espero que meus artigos sirvam como fonte de ideias e inspiração para os traders, ajudem a olhar para as coisas comuns com um olhar novo e renovado, bem como ajudem a escolher as ferramentas adequadas na busca de inter-relações complexas, ajudem a atingir metas e novos sucessos impressionantes.
Dê uma olhada nos sites em que as formas mais bem-sucedidas de visualizar dados comparativos foram desenvolvidas ao longo dos anos.
Veja os sites em que as opções mais bem-sucedidas de visualização de dados comparativos foram desenvolvidas ao longo dos anos.
Sim, um gráfico de barras (histograma) é uma boa maneira de exibir o que está sendo comparado, não há problema nisso.
Eu quis dizer que talvez valha a pena fornecer, além do histograma geral, também separadamente para cada teste (e há 9 deles). Uma tabela colorida é boa e permite que você identifique claramente as especificidades de cada algoritmo, mas não dá uma ideia de até que ponto eles diferem de uma disciplina para outra.
E, embora eu cite apenas algoritmos honestos (mesmo que alguns deles não sejam, eles são retrabalhados), ainda pode haver alguns que podem usar a repetibilidade nas funções de teste como uma "arma".
Recentemente, me deparei com um algoritmo desse tipo: os autores usaram a busca pelo mínimo na função Rastrigin, mas é absolutamente certo que o globo mínimo está em [0,0] (bem no centro da área de definição da função), com a "frieza" imaginária resultante desse algoritmo.
É por isso que estou trabalhando na ideia de revisar a metodologia de teste para me livrar da duplicação de funções bidimensionais em um espaço multidimensional e, ao mesmo tempo, preservar a possibilidade de visualizar o processo de teste - e essa é uma questão muito difícil, como pode parecer à primeira vista.
Andrei, onde você consegue isso?
Essa é uma pergunta que está em sua mente.
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Novo artigo Algoritmos de otimização populacionais: otimização de dinâmica espiral (Spiral Dynamics Optimization, SDO) foi publicado:
Neste artigo examinaremos a otimização de dinâmica espiral (SDO), um algoritmo de otimização baseado nos padrões de trajetórias espirais presentes na natureza, como nas conchas de moluscos. O algoritmo proposto pelos autores foi completamente repensado e modificado por mim, e o artigo discutirá por que essas mudanças foram necessárias.
O spiral dynamics optimisation (SDO) é um dos algoritmos físicos mais simples. Ele foi proposto por Tamura e Yasuda em 2011 e desenvolvido usando o fenômeno da espiral logarítmica presente na natureza. O algoritmo é simples e possui poucos parâmetros de controle. Além disso, possui alta velocidade de cálculo, capacidade de busca local, diversificação no início e intensificação em estágios posteriores.
Na natureza, existem muitas espirais, como galáxias, auroras boreais, chifres de animais, tornados, conchas marinhas, caracóis, amonitas, caudas de camaleões e cavalos-marinhos. As espirais também podem ser vistas na arte antiga criada pela humanidade no alvorecer de sua existência. Ao longo dos anos, diversos pesquisadores se esforçaram para entender as sequências espirais e suas complexidades, bem como desenvolver equações e algoritmos em torno delas. Além disso, vale ressaltar que um fenômeno espiral comum na natureza é a espiral logarítmica, que pode ser observada em galáxias e ciclones tropicais. Os processos discretos de geração da espiral logarítmica foram implementados como comportamento eficaz de busca em metaheurística, o que inspirou o desenvolvimento do algoritmo de otimização de dinâmica espiral.
Os padrões conhecidos como sequências espirais visíveis encontradas na natureza incluem plantas, árvores, ondas e muitas outras formas. Os padrões visuais na natureza podem ser modelados usando teoria do caos, fractais, espirais e outros conceitos matemáticos. Em alguns padrões naturais, as espirais e os fractais estão intimamente relacionados. Por exemplo, a espiral de Fibonacci é uma variação da espiral logarítmica baseada na proporção áurea e nos números de Fibonacci. Como é logarítmica, a curva tem a mesma aparência em todas as escalas, e também pode ser considerada um fractal.
Autor: Andrey Dik