Em outro projeto, fiz uma comparação entre o cálculo de erro rápido e o clássico em um loop de 20 a 50 linhas: (Presumo que você também tenha os mesmos erros acumulados em 50 mil linhas, em milhões de linhas ainda mais)
.
Primeiro comparei a olho nu 50 linhas de dados. Não há erros nelas.
Mas os erros são considerados como uma soma acumulativa. Em cada cálculo, podemos ter 1e-14 ... 1e-17 erros. Somando esses erros várias vezes, o erro total pode exceder 1e-5.
Fiz uma comparação mais profunda. Peguei 50.000 linhas e comparei os erros; se a diferença fosse grande, eu os colocaria na tela. O que obtive (veja abaixo).
Há erros individuais acumulados acima de 1e-4 (ou seja, diferenças na quarta casa decimal).
Portanto, a velocidade é certamente boa, mas se as cadeias de caracteres não forem 50 mil, mas 500 milhões? Receio que os resultados sejam absolutamente incomparáveis com o cálculo exato no loop.
fast_error= 9.583545e+02 true_error= 9.582576e+02
fast_error= 9.204969e+02 true_error= 9.204000e+02
fast_error= 8.814563e+02 true_error= 8.813594e+02
fast_error= 8.411763e+02 true_error= 8.410794e+02
fast_error= 7.995969e+02 true_error= 7.995000e+02
fast_error= 7.566543e+02 true_error= 7.565574e+02
fast_error= 7.246969e+02 true_error= 7.246000e+02
fast_error= 6.916562e+02 true_error= 6.915593e+02
fast_error= 6.574762e+02 true_error= 6.573793e+02
fast_error= 6.220969e+02 true_error= 6.220000e+02
fast_error= 5.854540e+02 true_error= 5.853571e+02
fast_error= 5.588969e+02 true_error= 5.588000e+02
fast_error= 5.313562e+02 true_error= 5.312593e+02
fast_error= 5.027762e+02 true_error= 5.026792e+02
fast_error= 4.730969e+02 true_error= 4.730000e+02
fast_error= 4.422538e+02 true_error= 4.421569e+02
fast_error= 4.205969e+02 true_error= 4.205000e+02
fast_error= 3.980561e+02 true_error= 3.979592e+02
fast_error= 3.745761e+02 true_error= 3.744792e+02
fast_error= 3.500969e+02 true_error= 3.500000e+02
fast_error= 3.245534e+02 true_error= 3.244565e+02
fast_error= 3.072969e+02 true_error= 3.072000e+02
fast_error= 2.892560e+02 true_error= 2.891591e+02
fast_error= 2.703760e+02 true_error= 2.702791e+02
fast_error= 2.505969e+02 true_error= 2.505000e+02
fast_error= 2.298530e+02 true_error= 2.297561e+02
fast_error= 2.164969e+02 true_error= 2.164000e+02
fast_error= 2.024559e+02 true_error= 2.023590e+02
fast_error= 1.876759e+02 true_error= 1.875789e+02
fast_error= 1.720969e+02 true_error= 1.720000e+02
fast_error= 1.556525e+02 true_error= 1.555556e+02
fast_error= 1.456969e+02 true_error= 1.456000e+02
fast_error= 1.351557e+02 true_error= 1.350588e+02
fast_error= 1.239757e+02 true_error= 1.238788e+02
fast_error= 1.120969e+02 true_error= 1.120000e+02
fast_error= 9.945174e+01 true_error= 9.935484e+01
fast_error= 9.239691e+01 true_error= 9.230000e+01
fast_error= 8.485553e+01 true_error= 8.475862e+01
fast_error= 7.677548e+01 true_error= 7.667857e+01
fast_error= 6.809691e+01 true_error= 6.800000e+01
fast_error= 5.875075e+01 true_error= 5.865385e+01
fast_error= 5.409691e+01 true_error= 5.400000e+01
fast_error= 4.905524e+01 true_error= 4.895833e+01
fast_error= 4.357517e+01 true_error= 4.347826e+01
fast_error= 3.759691e+01 true_error= 3.750000e+01
fast_error= 3.104929e+01 true_error= 3.095238e+01
fast_error= 2.829691e+01 true_error= 2.820000e+01
fast_error= 2.525480e+01 true_error= 2.515789e+01
fast_error= 2.187468e+01 true_error= 2.17777878e+01
fast_error= 1.809691e+01 true_error= 1.800000e+01
fast_error= 1.384691e+01 true_error= 1.375000e+01
fast_error= 1.249691e+01 true_error= 1.240000e+01
fast_error= 1.095405e+01 true_error= 1.085714e+01
fast_error= 9.173829e+00 true_error= 9.076923e+00
fast_error= 7.096906e+00 true_error= 7.000000e+00
fast_error= 4.642360e+00 true_error= 4.545455e+00
fast_error= 4.196906e+00 true_error= 4.100000e+00
fast_error= 3.652461e+00 true_error= 3.555556e+00
fast_error= 2.971906e+00 true_error= 2.875000e+00
fast_error= 2.096906e+00 true_error= 2.0000000000e+00
fast_error= 9.302390e-01 true_error= 8.33333333e-01
fast_error= 8.96909057e-01 true_error= 8.000000e-01
fast_error= 8.469057e-01 true_error= 7.500000e-01
fast_error= 7.635724e-01 true_error= 6.66666667e-01
fast_error= 5.969057e-01 true_error= 5.000000e-01
fast_error= 4.546077e+00 true_error= 4.545455e+00
fast_error= 4.100623e+00 true_error= 4.100000e+00
fast_error= 3.556178e+00 true_error= 3.555556e+00
fast_error= 2.875623e+00 true_error= 2.875000e+00
fast_error= 2.000623e+00 true_error= 2.000000e+00
fast_error= 8.339561e-01 true_error= 8.333333e-01
fast_error= 8.006228e-01 true_error= 8.000000e-01
fast_error= 7.506228e-01 true_error= 7.500000e-01
fast_error= 6.672894e-01 true_error= 6.66666667e-01
fast_error= 5.006228e-01 true_error= 5.000000e-01
Qual é o problema?
Durante o treinamento, o terminal trava e dá um erro, nem sempre, é como se fosse um tipo de poltergeist.
N 0 22:58:20.933 Core 1 2021.02.01 00:00:00 program string is NULL or empty
MP 0 22:58:20.933 Core 1 2021.02.01 00:00:00 A criação do programa OpenCL falhou. Error code=4003
CD 0 22:58:20.933 Core 1 2021.02.01 00:00:00 OnInit - 153 -> Error of reading EURUSD_PERIOD_H1_ 20AttentionMLMH_d.nnw prev Net 5015
RD 0 22:58:20.933 Core 1 2021.02.01 00:00:00 program string is NULL or empty
QN 0 22:58:20.933 Core 1 2021.02.01 00:00:00 Falha na criação do programa OpenCL. Error code=4003
IO 0 22:58:20.933 Core 1 final balance 10000.00 USD
LE 2 22:58:20.933 Core 1 2021.02.19 23:54:59 invalid pointer access in 'NeuroNet.mqh' (2271,16)
MS 2 22:58:20.933 Core 1 OnDeinit critical error
NG 0 22:58:20.933 Core 1 EURUSD,H1: 863757 ticks, 360 bars generated. Ambiente sincronizado em 0:00:00.018. O teste foi aprovado em 0:00:00.256.
QD 0 22:58:20.933 Core 1 EURUSD,H1: tempo total desde o login até a interrupção do teste 0:00:00.274 (incluindo 0:00:00.018 para a sincronização dos dados do histórico)
LQ 0 22:58:20.933 Core 1 321 Mb de memória usada, incluindo 0.47 Mb de dados de histórico, 64 Mb de dados de ticks
JF 0 22:58:20.933 Core 1 arquivo de registro "C:\Users\Buruy\AppData\Roaming\MetaQuotes\Tester\36A64B8C79A6163D85E6173B54096685\Agent-127.0.0.0.1-3000\logs\20210410.log" written
PP 0 22:58:20.939 Core 1 connection closed
Agradeço antecipadamente sua ajuda!
Dmitry, olá! Durante alguns meses, observei uma grande discrepância entre a execução do OOS e o trabalho final no mesmo intervalo, mas já com o EA. Todos os sinais são unificados (descarrego todos os sinais em um arquivo para cada barra e comparo). Há uma suspeita de que o processo de salvar e ler o treinamento não funciona corretamente. No arquivo NeuroNet.mph, para cada rede, é configurada uma maneira individual de salvar o treinamento
bool CNeuronProof::Save(const int file_handle)
bool CNeuronBase::Save(int file_handle)
bool CNeuronConv::Save(const int file_handle)
bool CNeuronLSTM::Save(const int file_handle)
bool CNeuronBaseOCL::Save(const int file_handle)
bool CNeuronAttentionOCL::Save(const int file_handle)
etc.
e o salvamento é usado
bool CNet::Save(string file_name,double error,double undefine,double forecast,datetime time,bool common=true)
Você pode explicar a diferença e é possível combinar os dados salvos com o treinamento da memória após uma época?
Dados de sinal de saída TempData e neurônios de saída ResultData no momento do treinamento
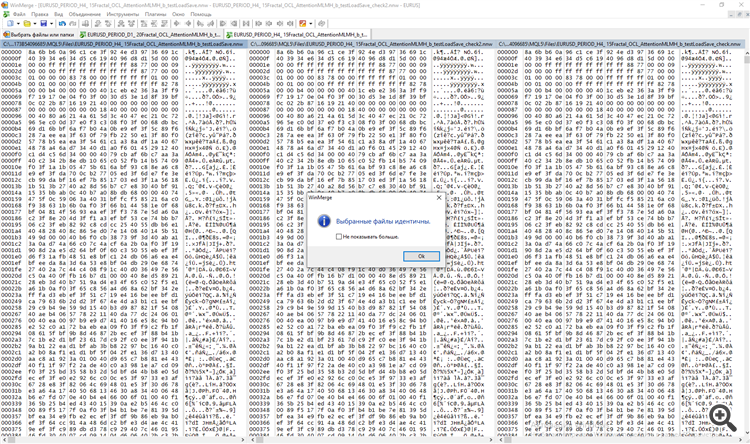
e separadamente no momento do teste. Comparei os dois arquivos no programa WinMerge.
Dmitry, olá! Durante alguns meses, observei uma grande discrepância entre a execução do OOS e o trabalho final no mesmo intervalo, mas já com o EA. Todos os sinais são unificados (descarrego todos os sinais em um arquivo para cada barra e comparo). Há uma suspeita de que o processo de salvar e ler o treinamento não funciona corretamente. No arquivo NeuroNet.mph, para cada rede, é configurada uma maneira individual de salvar o treinamento
bool CNeuronProof::Save(const int file_handle)
bool CNeuronBase::Save(int file_handle)
bool CNeuronConv::Save(const int file_handle)
bool CNeuronLSTM::Save(const int file_handle)
bool CNeuronBaseOCL::Save(const int file_handle)
bool CNeuronAttentionOCL::Save(const int file_handle)
etc.
e o salvamento é usado
bool CNet::Save(string file_name,double error,double undefine,double forecast,datetime time,bool common=true)
Você pode explicar a diferença e é possível combinar os dados salvos com o treinamento da memória após uma época?
Dados de sinal de saída TempData e neurônios de saída ResultData no momento do treinamento
e separadamente no momento do teste. Comparei os dois arquivos no programa WinMerge.
Bom dia, Dmitry.
Vamos dar uma olhada no método CNet::Save(...). Depois de registrar as variáveis que caracterizam o estado de treinamento da rede, o método Save da matriz de camadas neurais (CArrayLayer herdada de CArrayObj) é chamado
bool CNet::Save(string file_name,double error,double undefine,double forecast,datetime time,bool common=true) { if(MQLInfoInteger(MQL_OPTIMIZATION) || MQLInfoInteger(MQL_TESTER) || MQLInfoInteger(MQL_FORWARD) || MQLInfoInteger(MQL_OPTIMIZATION)) return true; if(file_name==NULL) return false; //--- int handle=FileOpen(file_name,(common ? FILE_COMMON : 0)|FILE_BIN|FILE_WRITE); if(handle==INVALID_HANDLE) return false; //--- if(FileWriteDouble(handle,error)<=0 || FileWriteDouble(handle,undefine)<=0 || FileWriteDouble(handle,forecast)<=0 || FileWriteLong(handle,(long)time)<=0) { FileClose(handle); return false; } bool result=layers.Save(handle); FileFlush(handle); FileClose(handle); //--- return result; }
A classe CArrayLayer não tem método Save, portanto, o método da classe pai CArrayObj::Save(const int file_handle) é chamado . O corpo desse método contém um loop para enumerar todos os objetos aninhados e chamar o método Save para cada objeto.
//+------------------------------------------------------------------+ //| Gravação da matriz no arquivo| //+------------------------------------------------------------------+ bool CArrayObj::Save(const int file_handle) { int i=0; //--- verificação if(!CArray::Save(file_handle)) return(false); //--- escrever o comprimento da matriz if(FileWriteInteger(file_handle,m_data_total,INT_VALUE)!=INT_VALUE) return(false); //--- escrever matriz for(i=0;i<m_data_total;i++) if(m_data[i].Save(file_handle)!=true) break; //--- resultado return(i==m_data_total); }
Em outras palavras, o princípio de um boneco de aninhamento é usado aqui: chamamos o método Save para o objeto de nível superior e, dentro do método, todos os objetos aninhados são pesquisados e o método com o mesmo nome é chamado para cada objeto.
O carregamento de dados de um arquivo é organizado de forma semelhante.
Com relação às diferentes avaliações durante o treinamento e a operação. Não sei como a sua rede neural está organizada no modo de operação, mas no modo de treinamento os parâmetros da rede neural mudam constantemente. Dessa forma, os mesmos dados de entrada produzirão resultados diferentes.
Atenciosamente,
Dmitry.
P.S. Para verificar a exatidão do salvamento e da leitura de dados, crie um pequeno programa de teste no qual você possa ler a rede neural de um arquivo e salvá-la imediatamente em um novo arquivo. Em seguida, compare os dois arquivos. Se notar alguma discrepância, escreva-me e eu verificarei.
Boa tarde, Dmitry.
Vamos dar uma olhada no método CNet::Save(...). Depois de registrar as variáveis que caracterizam o estado de treinamento da rede, o método Save da matriz de camadas neurais (CArrayLayer herdada de CArrayObj) é chamado
A classe CArrayLayer não tem método Save, portanto, o método da classe pai CArrayObj::Save(const int file_handle) é chamado . O corpo desse método contém um loop para enumerar todos os objetos aninhados e chamar o método Save para cada objeto.
Em outras palavras, o princípio de um boneco de aninhamento é usado aqui: chamamos o método Save para o objeto de nível superior e, dentro do método, todos os objetos aninhados são pesquisados e o método com o mesmo nome é chamado para cada objeto.
O carregamento de dados de um arquivo é organizado de forma semelhante.
Com relação às diferentes avaliações durante o treinamento e a operação. Não sei como sua rede neural está organizada no modo de operação, mas no modo de treinamento os parâmetros da rede neural mudam constantemente. Dessa forma, os mesmos dados de entrada produzirão resultados diferentes.
Atenciosamente,
Dmitry.
P.S. Para verificar a exatidão do salvamento e da leitura de dados, crie um pequeno programa de teste no qual você possa ler a rede neural de um arquivo e salvá-la imediatamente em um novo arquivo. Em seguida, compare os dois arquivos. Se notar alguma discrepância, escreva-me e eu verificarei.
Aceito, tentarei verificar da seguinte forma. Na primeira barra, salvarei TempData (Signals) e OUTPUT Neurons no arquivo. Primeiro, sem carregar o arquivo, mas com treinamento; depois, com o carregamento do treinamento a partir da mesma primeira barra, mas sem treinamento no processo. Eu escreverei de volta.
p/s/ já que no processo de treinamento realmente aprendemos a neuronka em cada barra, no processo do testador implementamos o mesmo processo, mas com N barras a menos. o impacto não deve ser significativo. Mas eu concordo que deveria ser.
Prezado Dmitry!
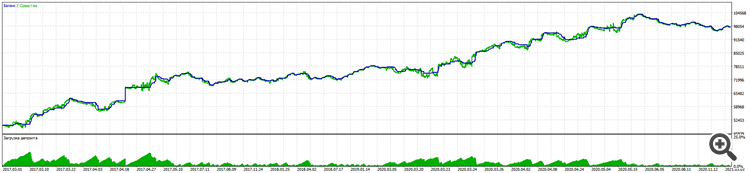
No processo de um longo trabalho com a ajuda de sua biblioteca, consegui criar um consultor de negociação com um bom resultado de 11% de redução para quase 100% de ganho para EURUSD de 5 anos.
Alpari:
O teste em uma conta real segue a mesma lógica.
É digno de nota que, mesmo em futuros BKS, o RURUSD oferece resultados ainda melhores com as mesmas entradas. (Ainda não testei em outros pares).
A principal vitória foi testar a negociação às cegas (treinar apenas nos períodos anteriores) e o Stoploss obrigatório sem martingales e outros truques, exceto pelo direito de abrir várias negociações em qualquer direção, dependendo do sinal.
É claro que tive de estudar e complementar muito com os cursos de cinco semanas nas Universidades WSE e Stanford, e muitos artigos sobre redes neurais, especialmente para entender o que ensinar, o que ensinar e como ensinar.
Muito obrigado!
Por favor, não parem e continuem a desenvolver a biblioteca.
O que eu gostaria de pedir que você pensasse sobre
1. Ainda sobre a preservação do treinamento. Como já escrevi, ele não funciona. Você precisa aprender sempre e "de cara", sem parar de negociar. Isso não é um problema, o treinamento é rápido, mas há um segundo problema.
2. No início, você definiu a lógica Randomise para criar neurônios primários. Isso leva a até três versões de treinamento. (Acho que o ponto principal é que o neurônio primário é inicialmente positivo ou negativo).
Sim, isso também pode ser resolvido, por assim dizer, forçando o retreinamento, a partir do zero, se você não chegar às métricas corretas.
Mas tenho certeza de que você pode começar com um peso condicional de 0,01 em cada neurônio. (Infelizmente, o excesso de treinamento se torna mais pronunciado).
Ou ainda aprender a manter a melhor cópia da educação, então é o ponto 1.
Caro Dimitri!
No processo de um longo trabalho com a ajuda de sua biblioteca, consegui criar um consultor de negociação com um bom resultado de 11% de redução para quase 100% de ganho para EURUSD de 5 anos.
Alpari:
O teste em uma conta real segue a mesma lógica.
Vale ressaltar que, mesmo em futuros de BKS, o RURUSD apresenta resultados ainda melhores com as mesmas entradas. (Ainda não testei em outros pares).
A principal vitória foi testar a negociação às cegas (treinamento somente em períodos passados) e o Stoploss obrigatório sem martingales e outros truques, exceto pelo direito de abrir várias negociações em qualquer direção, dependendo do sinal.
É claro que tive de estudar e complementar muitas coisas dos cursos de cinco semanas nas Universidades WSE e Stanford e muitos artigos sobre redes neurais, especialmente para entender o que ensinar, o que ensinar e como ensinar.
Muito obrigado!
Por favor, não parem e continuem o desenvolvimento da biblioteca.
O que eu gostaria de pedir a vocês que pensassem sobre
1. Ainda sobre a preservação do treinamento. Como já escrevi, isso não funciona. Você precisa aprender sempre e "de cara", sem parar de negociar. Isso não é um problema, o treinamento é rápido, mas há um segundo problema.
2. No início, você definiu a lógica Randomise para criar neurônios primários. Isso leva a até três versões de treinamento. (Acho que o ponto principal é que o neurônio primário é inicialmente positivo ou negativo).
Sim, você também pode combater isso, por assim dizer, forçando o retreinamento, do zero, se não tiver atingido as métricas necessárias.
Mas tenho certeza de que você pode começar com um peso condicional de 0,01 em cada neurônio. (Infelizmente, o excesso de treinamento se torna mais pronunciado)
Ou ainda aprender a manter a melhor cópia da educação, então é o ponto 1.
Obrigado, Dimitri, por suas palavras gentis. Iniciar todos os pesos com um valor constante é uma prática ruim. Nesse caso, durante o aprendizado, todos os neurônios funcionam sincronizadamente como um só. E a rede neural inteira se degenera em um neurônio em cada camada.
....
O que eu gostaria de pedir a você para pensar
1. Ainda sobre manter o treinamento. Como já escrevi, isso não funciona. Você precisa aprender sempre e "de cara", sem parar de negociar. Isso não é um problema, o aprendizado é rápido, mas há um segundo problema.
2. No início, você definiu a lógica Randomise para criar neurônios primários. Isso leva a até três versões de treinamento. (Acho que o ponto principal é que o neurônio primário é inicialmente positivo ou negativo).
Sim, você também pode combater isso, por assim dizer, forçando o retreinamento, do zero, se não tiver atingido as métricas necessárias.
Mas tenho certeza de que você pode começar com um peso condicional de 0,01 em cada neurônio. (Infelizmente, o excesso de treinamento se torna mais pronunciado)
Ou ainda aprender a manter a melhor cópia da educação, então é o ponto 1.
Dimitri, eu testei isso como o autor aconselhou.
1. Treine várias épocas e, após cada época, o arquivo de rede é salvo.
2. Exclua do gráfico. Execute novamente com o parâmetro testSaveLoad ativado - depois de ler a rede treinada anteriormente, o Expert Advisor a grava novamente, repete o ciclo de leitura-escrita novamente e descarrega, e obtemos três arquivos, além da rede original com os prefixos _check e _check2.
3. Comparamos os três arquivos. a) aprendemos a programar por meio de testes b) procuramos erros em nós mesmos.
Obrigado, Alexei, mas não publiquei os resultados aqui.
O problema estava em outro lugar.
O processo de salvar/carregar funciona.
A solução foi encontrada na linha de criação de elementos de rede de neurônios usando Randomize.
bool CArrayCon::CreateElement(int index) { if(index<0 || index>=m_data_max) return false; //--- xor128; double weigh=(double)rnd_w/UINT_MAX-0.5; m_data[index]=new CConnection(weigh); if(!CheckPointer(m_data[index])!=POINTER_INVALID) return false; //--- return (true); }
Eu a substituí por uma função mais estável de criação de neurônios, e é importante criar um número igual de neurônios positivos e negativos, para que a rede não seja predisposta a vendas ou compras.
double weigh=(double)MathMod(index,0)?sin(index):sin(-index);
Fiz o mesmo com a função de criação de pesos iniciais, por precaução.
double CNeuronBaseOCL::GenerateWeight(void) { xor128; double result=(double)rnd_w/UINT_MAX-0.5; //--- return result; } //+----
Agora, o backtest apresenta o mesmo resultado ao testar a rede treinada depois de carregar o arquivo de treinamento.
As entradas são unidades por segundo.
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Novo artigo Redes neurais de maneira fácil (Parte 13): normalização em lote foi publicado:
No artigo anterior, começamos a examinar métodos para melhorar a qualidade do treinamento da rede neural. Neste artigo, proponho continuar este tópico e considerar uma outra abordagem, em particular a de normalização de dados em lote.
A prática da utilização de redes neurais aplica diferentes abordagens à normalização de dados. Mas todas elas visam manter os dados da amostra de treinamento e os dados de saída das camadas ocultas da rede neural dentro de um determinado intervalo e com certas características estatísticas da amostra, tais como variância e mediana. Por que isso é tão importante se, afinal, lembramos que os neurônios da rede aplicam transformações lineares, que no processo de treinamento deslocam a amostra para o antigradiente?
Consideremos um perceptron totalmente conectado com 2 camadas ocultas. Durante a passagem para frente, cada camada gera um determinado conjunto de dados que serve como uma amostra de treinamento para a próxima camada. O resultado da camada de saída é comparado com os dados de referência, enquanto o gradiente de erro desde a camada de saída através das camadas ocultas até os dados de origem é propagado na passagem para atrás. Dado um gradiente de erro diferente em cada neurônio, atualizamos os coeficientes de peso ajustando nossa rede neural às amostras de treinamento da última passagem para frente. E aqui surge um conflito: ajustamos a segunda camada oculta (H2 na figura abaixo) para a amostra de dados na saída da primeira camada oculta (na figura H1), enquanto já alteramos a matriz de dados alterando os parâmetros da primeira camada oculta. ajustamos a segunda camada oculta a uma amostra de dados que ainda não existe. A situação é semelhante com a camada de saída, que se ajusta à saída já modificada da segunda camada oculta. E se considerarmos também a distorção entre a primeira e a segunda camada oculta, a escala do erro aumenta. E quanto mais profunda for a rede neural, mais forte será a manifestação deste efeito. Este fenômeno tem sido denominado de mudança de covariância interna.
Nas redes neurais clássicas, esse problema foi parcialmente resolvido pela redução da taxa de aprendizado. Pequenas mudanças nos coeficientes de peso não alteram significativamente a distribuição da amostragem na saída da camada neural. Mas essa abordagem não resolve o problema de dimensionamento com um aumento no número de camadas da rede neural e reduz a taxa de aprendizado. Outro problema de uma pequena taxa de aprendizado é ficar preso em mínimos locais, já falamos sobre isso no artigo [6]
Autor: Dmitriy Gizlyk