Bibliotecas: Biblioteca multiplataforma de funções matemáticas originais

Novo comentário
 

Biblioteca multiplataforma de funções matemáticas originais:

Funções matemáticas originais - vistas de diferentes perspetivas - que não têm homólogos ora realizam seu trabalho muito mais rápido do que implementações alternativas

Autor: fxsaber

 
Por favor, implemente o teste ADF e outros testes para verificar a cointegração.
[Excluído]  
Outro presente do fxsaber, obrigado)
  
// O indicador mostra o grau de similaridade de cada intervalo histórico com o intervalo atual

#property indicator_separate_window

#property indicator_buffers 1
#property indicator_plots 1

#property indicator_minimum -1
#property indicator_maximum 1

#property  indicator_color1 clrRed
#property  indicator_type1 DRAW_LINE
#property  indicator_width1 2

sinput int Amount = 100; // Número dos últimos compassos (Pattern)

#include <fxsaber\Math\Math.mqh> // https://www.mql5.com/pt/code/17982

double Buffer[];

void OnInit()
{
  SetIndexBuffer(0, Buffer);
}

int OnCalculate( const int rates_total,
                 const int prev_calculated,
                 const datetime &time[],
                 const double &open[],
                 const double &high[],
                 const double &low[],
                 const double &close[],
                 const long &tick_volume[],
                 const long &volume[],
                 const int &spread[] )
{
  if (rates_total > prev_calculated)
  {
    double Pattern[];
    
    ArrayCopy(Pattern, open, 0, rates_total - Amount, Amount);
    
    MathCorrelationPearson(open, Pattern, Buffer);
    
    const int Pos = ArrayMaximum(Buffer, 0, rates_total - Amount);
    
    Comment("O trecho mais semelhante da história correspondente ao mais recente (" +
          (string)time[rates_total - 1] + ") " + (string)Amount + "Baram, está aqui." +
          (string)time[Pos] + " - QI de Pearson = " + (string)Buffer[Pos]);
  }
  
  return(rates_total);
}

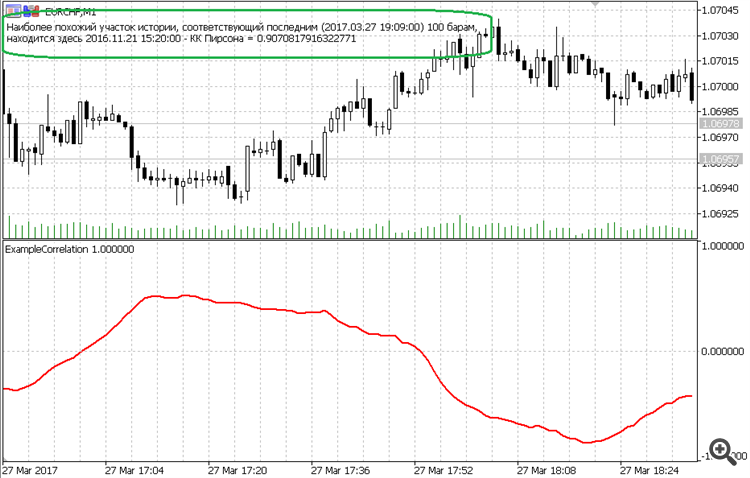
Um exemplo de como você pode encontrar rapidamente o trecho de história mais semelhante (de acordo com Pearson).

O ponto forte da implementação está apenas no algoritmo - muito mais rápido do que qualquer outro.

 
fxsaber:

Um exemplo de como você pode encontrar rapidamente o trecho de história mais semelhante (de acordo com Pearson).

O ponto forte da implementação está apenas no algoritmo - muito mais rápido do que qualquer outro.


No histórico, isso é bom. Mas eu gostaria de fazer o contrário, selecionar vários fragmentos de barras no histórico, e o indicador nos notificaria sobre isso se visse coincidências. Em princípio, essa implementação é possível?
 
s22aa:

No histórico, isso é bom. Mas eu gostaria de fazer o contrário, selecionar vários fragmentos de barras no histórico, e o indicador nos notificaria sobre isso se visse coincidências. Em princípio, essa implementação é possível?
Um simples MathCorrelationPearson padrão será suficiente para isso.
 
fxsaber:
Um simples MathCorrelationPearson interno será suficiente.

Bem, isso é ótimo. Acabei de começar a estudar C++ em cursos, já passei por ciclos e me sinto quase um guru da programação, bem, não exatamente um guru, é claro, mas na metade do caminho, um meio-ganso em uma palavra. Acho que em alguns anos o MathCorrelationPearson padrão também será "simples" para mim.
  
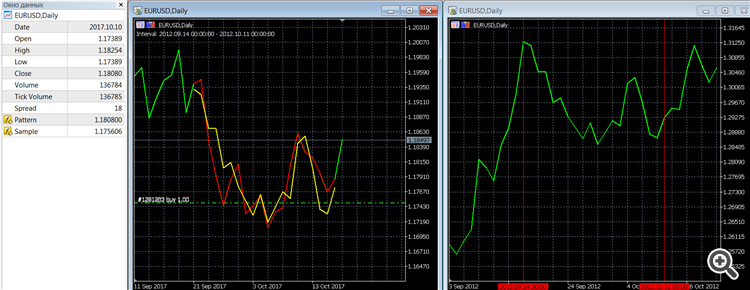
// Exemplo de como encontrar o intervalo "mais semelhante" ao atual (critério QC de Pearson).
#property indicator_chart_window

#property indicator_buffers 2
#property indicator_plots 2

#property  indicator_color1 clrRed
#property  indicator_type1 DRAW_LINE
#property  indicator_width1 2

#property  indicator_color2 clrYellow
#property  indicator_type2 DRAW_LINE
#property  indicator_width2 2

sinput int inAmount = 20;   // Número dos últimos compassos (Pattern)
input int  inMaxBars = 1 e5; // Número de barras a serem analisadas

#include <fxsaber\Math\Math.mqh> // https://www.mql5.com/pt/code/17982

double Buffer0[];
double Buffer1[];
double Buffer2[];
int handle;

const long handleChart = ChartOpen(_Symbol, PERIOD_CURRENT);

void OnInit()
{
  SetIndexBuffer(0, Buffer0);
  SetIndexBuffer(1, Buffer1);

  PlotIndexSetString(0, PLOT_LABEL, "Pattern");
  PlotIndexSetString(1, PLOT_LABEL, "Sample");
  
  ChartSetInteger(handleChart, CHART_MODE, CHART_LINE);
  ChartSetInteger(handleChart, CHART_AUTOSCROLL, false);  
}

//------
// Extraído de Include\Math\Stat\Math.mqh - https://www.mql5.com/ru/forum/97153/page15#comment_5927026

const double QNaN   =(double)"nan";   // QNaN.

//+------------------------------------------------------------------+
//| Calcula o valor médio dos valores no array[] |.
//+------------------------------------------------------------------+
double MathMean(const double &array[])
  {
   int size=ArraySize(array);
//--- verificar o intervalo de dados
   if(size<1)
      return(QNaN); // precisa de pelo menos 1 observação
//--- calcular a média
   double mean=0.0;
   for(int i=0; i<size; i++)
      mean+=array[i];
   mean=mean/size;
//--- return mean
   return(mean);
  }
//+------------------------------------------------------------------+
//| Calcula a variância dos valores no array[] |.
//+------------------------------------------------------------------+
double MathVariance(const double &array[])
  {
   int size=ArraySize(array);
//--- verificar o intervalo de dados
   if(size<2)
      return(QNaN); // precisa de pelo menos 2 observações
//--- calcular a média
   double mean=0.0;
   for(int i=0; i<size; i++)
      mean+=array[i];
   mean=mean/size;
//--- calcular a variância
   double variance=0;
   for(int i=0; i<size; i++)
      variance+=MathPow(array[i]-mean,2);
   variance=variance/size;
//--- variação de retorno
   return(variance);
  }
//------

// Adaptação da amostra ao padrão
void NormalizeArray( const double &Pattern[], double &Sample[], const bool Reverse = false )
{
  const double MeanPattern = MathMean(Pattern);
  const double MeanSample = MathMean(Sample);
  const double Koef = (Reverse ? -1 : 1) * MathSqrt(MathVariance(Pattern) / MathVariance(Sample));
  
  const int Total = ArraySize(Pattern);
  
  for (int i = 0; i < Total; i++)
    Sample[i] = (Sample[i] - MeanSample) * Koef + MeanPattern;
}

void MathLog( double &Array[] )
{
  for (int i = ArraySize(Array) - 1; i >= 0; i--)
    Array[i] = MathLog(Array[i]);
}

void MathExp( double &Array[] )
{
  for (int i = ArraySize(Array) - 1; i >= 0; i--)
    Array[i] = MathExp(Array[i]);
}

// Encontra a melhor amostra por padrão
int GetSample1( const int Amount, const double &Prices[], double &Sample[], double &Pattern[], int MaxBars )
{
  const int Total = ArraySize(Prices) - 1; // Remova a última barra dos cálculos
    
  ArrayCopy(Pattern, Prices, 0, Total - Amount, Amount);

  MaxBars = (Total > MaxBars) ? MaxBars : Total;
  
  double Prices2[];
  ArrayCopy(Prices2, Prices, 0, Total - MaxBars, MaxBars);  
  MathLog(Prices2);
  
  double Pattern2[];
  ArrayCopy(Pattern2, Pattern);  
  MathLog(Pattern2);
    
  double Pearson[];  
  MathCorrelationPearson(Prices2, Pattern2, Pearson);
  
  const int PosMax = ArrayMaximum(Pearson, 0, MaxBars - Amount);  
  const int PosMin = ArrayMaximum(Pearson, 0, MaxBars - Amount);  
  
  const bool Res = (MathAbs(Pearson[PosMax]) < MathAbs(Pearson[PosMin]));
  const int Pos2 = Res ? PosMin : PosMax;

  ArrayCopy(Sample, Prices2, 0, Pos2 - Amount + 1, Amount);
  NormalizeArray(Pattern2, Sample, Res);  
  MathExp(Sample);
      
  return(Pos2 + Total - MaxBars);
}

void OnDeinit( const int )
{
  ChartClose(handleChart);
}

int OnCalculate( const int rates_total,
                 const int prev_calculated,
                 const datetime &time[],
                 const double &open[],
                 const double &high[],
                 const double &low[],
                 const double &close[],
                 const long &tick_volume[],
                 const long &volume[],
                 const int &spread[] )
{
  if (rates_total > prev_calculated)
  {       
    double Pattern[];
    double Sample[];
    
    const int Pos = GetSample1(inAmount, close, Sample, Pattern, inMaxBars);   
    
    // Derivamos o próprio padrão
    ArrayInitialize(Buffer0, EMPTY_VALUE);
    ArrayCopy(Buffer0, Pattern, rates_total - inAmount - 1);

    // Amostra de saída
    ArrayInitialize(Buffer1, EMPTY_VALUE);
    ArrayCopy(Buffer1, Sample, rates_total - inAmount - 1);
    
    Comment("Interval: " + (string)time[Pos - inAmount + 1] + " - " + (string)time[Pos]);
  
    // Mostrar a seção encontrada
    const int Offset = 10;
    ChartNavigate(handleChart, CHART_BEGIN, Pos - inAmount + 1 - Offset); // Deslocar o gráfico por barras de deslocamento antes do início da fonte de amostragem
    ObjectCreate(handleChart, "Left", OBJ_VLINE, 0, time[Pos - inAmount + 1], 0);
    ObjectCreate(handleChart, "Right", OBJ_VLINE, 0, time[Pos], 0);    
  }
  
  return(rates_total);
}

 

Tentei compilar o código e obtive erros:

não é possível abrir o arquivo de inclusão "C:\Program Files\Alpari MT4\MQL4\include\fxsaber\Math\Math\Math.mqh" ... 18 11

'i' - variável já definida 77 12

'MathCorrelationPearson' - função não definida 128 3

Por que isso acontece?



 
YarTrade:

Tentei compilar o código e obtive erros:

não é possível abrir o arquivo de inclusão "C:\Program Files\Alpari MT4\MQL4\include\fxsaber\Math\Math\Math.mqh" ... 18 11

'i' - variável já definida 77 12

'MathCorrelationPearson' - função não definida 128 3

Por quê?

Escreva a diretriz

#property strict
12
Novo comentário