記事「非線形指標」についてのディスカッション

新しいコメント
 

新しい記事「非線形指標」はパブリッシュされました:

今回は、非線形指標を構築する方法と取引での使用について、いくつか考えてみたいと思います。MetaTraderの取引プラットフォームには、非線形なアプローチを使用する指標がかなりあります。

最頻値は、データサンプルの中で最も頻繁に出現する値です。例えば、サンプル1, 6, 9, 3, 3, 7, 8では、最も多い数字は3で、これが最頻値となります。ただし、価格を分析する場合、各値は一度しか発生しないため、最頻値を計算するためには、Pearsonの経験式を用いることができます。

Mode = 3*Median – 2*Mean

この式によると、最頻値は不安定な指標です（係数が区間-1...+1の境界を越えている）が、他の指標に加えるものとして有用です。

もう1つの中心的な指標は、その中間と考えることができます。これを計算するには、時系列の最大値と最小値の半値和を求める必要があります。ミドルレンジはスパイクに敏感で信頼性が低いですが、一部の指標で使用されています。

中心的傾向を示す4つの指標すべては、チャート上では次のようになります。


作者: Aleksej Poljakov

 

面白いアイデアだ。:)

記事をありがとう！

 


それは奇妙だ。

インジケーターと一致しない。

何か誤解していたのかもしれない。

 
Nikolai Semko #:


それは奇妙だ。

と一致しない。

インジケーターはこちら

何か誤解していたのかもしれない。

中央値は移動平均線と常に一致するわけではありません。むしろ、一致しないことがほとんどです。中央値は硬直的な構造です（例えば、中央値に沿ってトレンドラインを引くと、まったく異なる図が得られます）。

そして、中央値が短い期間でも非常に安定しているため、一致しないことが起こるのです。あなたのインジケータとベイズ平滑化を比較してみてください。

 
Aleksej Poljakov #:

中央値と移動平均は必ずしも一致しない。むしろ、一致しないことが多い。中央値の中央値は硬直的な構造である（例えば、それに沿ってトレンドラインを引くと、まったく異なるイメージになる）。

そして、一致しないことが起こるのは、まさに中央値が非常に安定しているからであり、たとえ短い期間であっても......。あなたのインジケータとベイズ平滑化を比較してみてください。

ああ、そうだ、注意していなかった。
それにしても何かおかしい。
私が理解しているように、このような計算では、インジケータの現在の値（3の3）は、5つ前の価格値のいずれかになるはずですが、これは近いものでもありません。一般的に、とんでもないタイムラグがある。
今のところ、あなたのチャートからは何をつかむべきかわかりません。他のスムージングに比べて、ラグが少ない利点は何ですか？
 
Nikolai Semko #:
ああ、そうだ、注意していなかった。
でも、まだ何かおかしい。
私が理解しているように、この計算では、インジケータの現在値（3/3）は5つ前の価格値のいずれかになるはずですが、これは全然違います。一般的に、とんでもないタイムラグがある。
今のところ、あなたのチャートからは何をつかめばいいのかわかりません。他のスムージングに比べて ラグが少ない利点は何ですか？



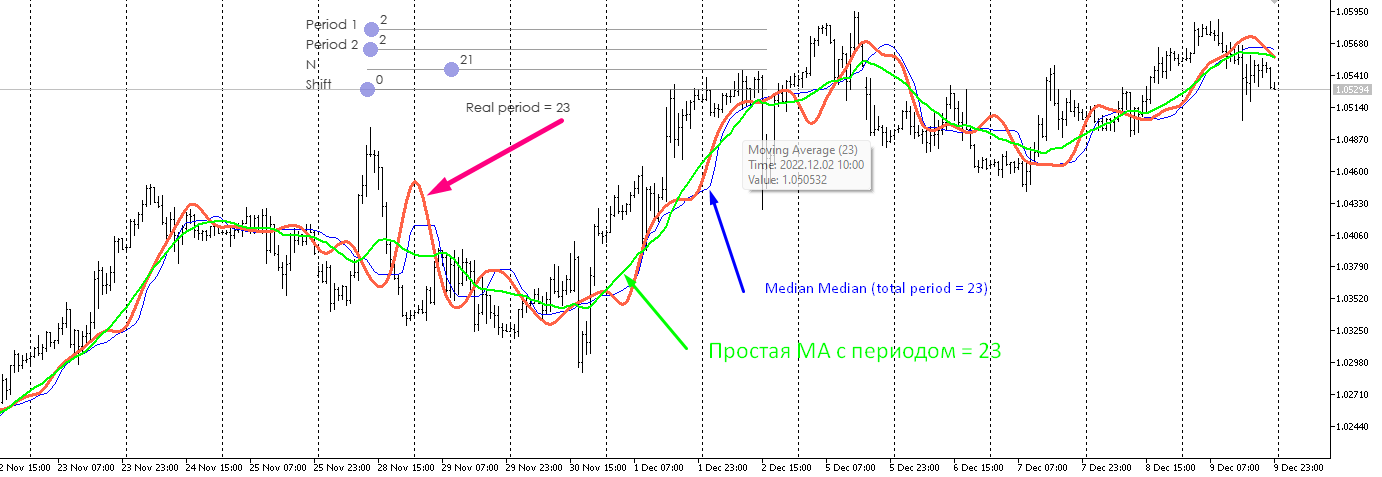
あることが書いてあるが、グラフは別のことを示している。 つまり、インジケーターは直近の23の値から1つの値を示しています。 私はそれを分析し、他の移動タイプと比較しました。残念ながら、ソートによる計算負荷が著しく高いにもかかわらず、利点は見つかりませんでした。



あるサイズ（期間）の過去のデータを使って、足し算、掛け算、割り算、度数を増やす、対数を取るなど、新しい線を引くためにあらゆる操作を試みても、今のところ意味がありません。なぜなら、これら数多くの指標（線）はすべて、コインを投げて出た目の確率に近い確率で、次のバー（下降または上昇）のさらなる値動きを予測するからです。これは簡単に確認でき、証明できます。

 
Nikolai Semko #:



あることが書いてありますが、チャート上ではまったく違います。 つまり、インジケーターは直近の23の値から1つの値を示している。 それを分析し、他のスライドと比較した。残念ながら、並べ替えによる計算負荷の大幅な上昇にもかかわらず、利点は見つかりませんでした。


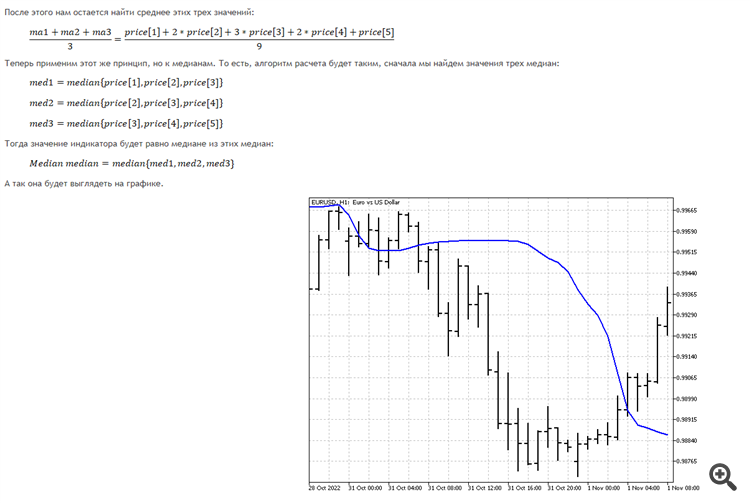
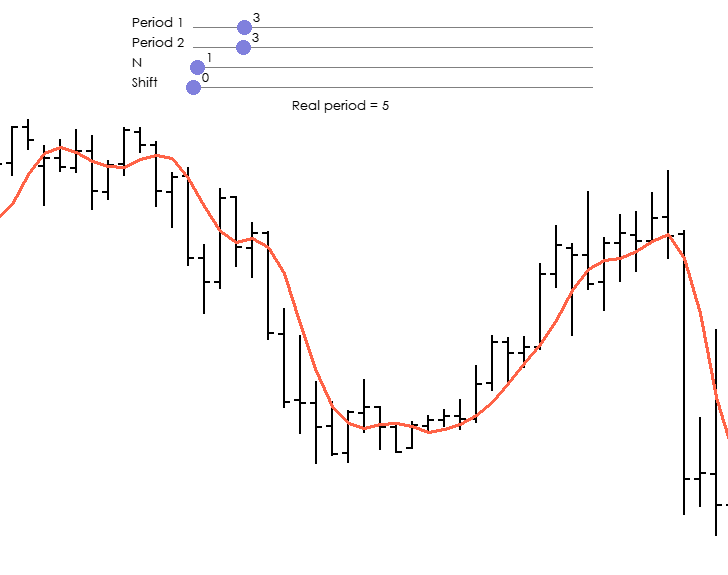
この形の中央値を三角形のウィンドウで比較する方がよい。最も "おいしい "状況は、トレンドの方向が反対に変わることである。より敏感な変化が必要な場合は、この方法で行うのがよい。最初に最後の1つの価格から中央値を求め、次に2つの価格から中央値を求め、次に3つの価格から求める。最後に、以前に見つけたすべての価格の中央値を求めます。線形加重平均のアナログが得られる。これは、中央値の主な欠点である端の情報の損失を取り除くことはできませんが、現在の変化に対してより敏感な指標になります。

 
Aleksej Poljakov #:

この形の中央値は、三角窓よりも優れている。最も "おいしい "状況は、トレンドの方向が反対に変わることである。より敏感なバリエーションが必要な場合は、この方法で行うのがよいでしょう。最初に最後の1つの価格から中央値を求め、次に2つの価格から中央値を求め、次に3つの価格から求める。最後に、以前に見つけたすべての価格の中央値を求めます。線形加重平均のアナログが得られる。これは、中央値の主な欠点である端の情報の損失を取り除くことはできませんが、現在の変化に対してより敏感な指標になります。


何年も前に、クラスタリングや平均化のさまざまな方法を開発し、それらを応用した何百台ものロボットを作ろうとした私の試みがすべて無駄だったように。信じてほしい、私はこれでずっと成功したのだ。
パターンとプロセスを認識するAIだけが残っている。
地団駄を踏まなければ、いずれそこにたどり着くだろう。

 
Nikolai Semko #:
ああ、そうだ、注意していなかった。
でも、まだ何かおかしい。
私が理解しているように、この計算では、インジケータの現在値（3/3）は5つ前の価格値のいずれかになるはずですが、これは全然違います。一般的に、とんでもないタイムラグがある。
今のところ、あなたのチャートからは何をつかめばいいのかわかりません。他のスムージングに比べて、ラグが少ない利点は何ですか？

ラグと戦いたければ、適切なモデルを使わなければならない。例えば、3次の多項式を20ポイント前方へプロットします。係数{4979,3264,1904,864,109,-396,-686,-796,-761,-616,-396,-136,129,364,534,604,539,304,-136,-816}/8855が 得られます。

 
Aleksej Poljakov #:

ラグに苦戦する場合は、適切なモデルを取る必要がある。例えば、3次の多項式を20ポイント前方で構成する。係数{4979,3264,1904,864,109,-396,-686,-796,-761,-616,-396,-136,129,364,534,604,539,304,-136,-816}/8855が 得られます。

とっくにすべてが実装され、チェック、再チェック、テスト、再テストされています。魚はいない。より正確には、魚の存在は常に一時的なものであり、残りの時間は一時的な成功を平準化する。


 
Aleksej Poljakov #:

ラグに苦戦する場合は、適切なモデルを取る必要がある。例えば、3次の多項式を20ポイント前方で構成する。係数{4979,3264,1904,864,109,-396,-686,-796,-761,-616,-396,-136,129,364,534,604,539,304,-136,-816}/8855が 得られます。

多項式そのものは再描画されるため、値はそのトレースとなり、描画されないスライディング・ラインを形成する。
確かに、最小の遅れを達成することは可能だが、他の問題が始まる。

取引、自動取引システム、取引戦略のテストに関するフォーラム。

Lsma

ニコライ・セムコ, 2020.02.01:09

単純移動平均（期間200）：



線形回帰からの移動平均（期間200）：


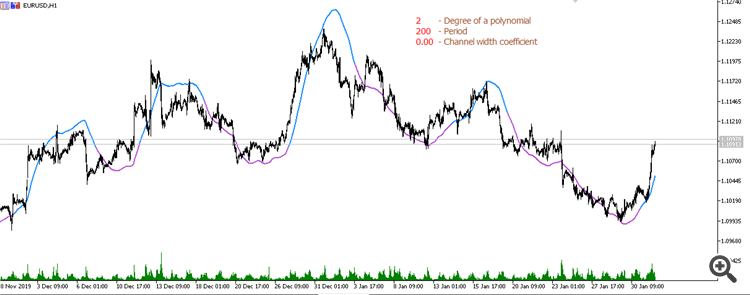
放物線回帰からの移動平均（期間200）：


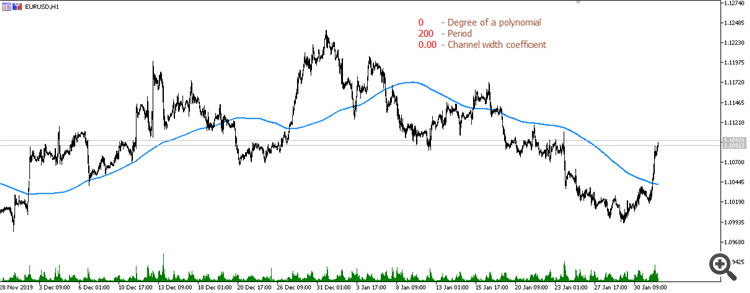
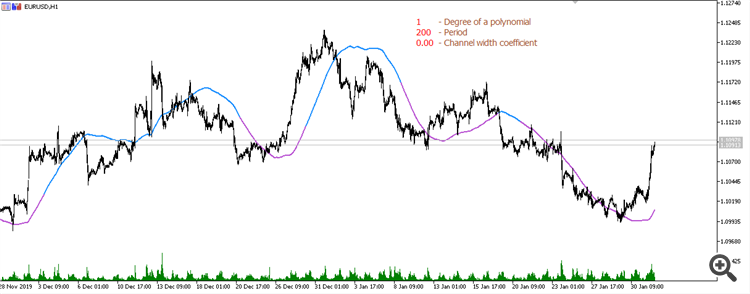
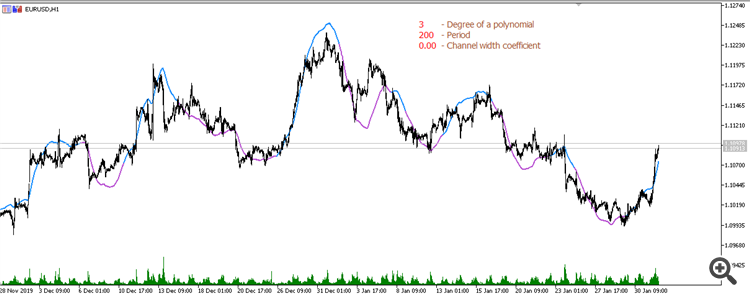
3次多項式からの移動平均（期間200）：

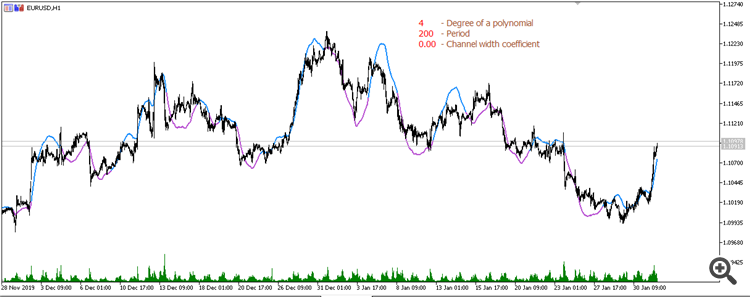
4次多項式からの移動平均（期間200）：

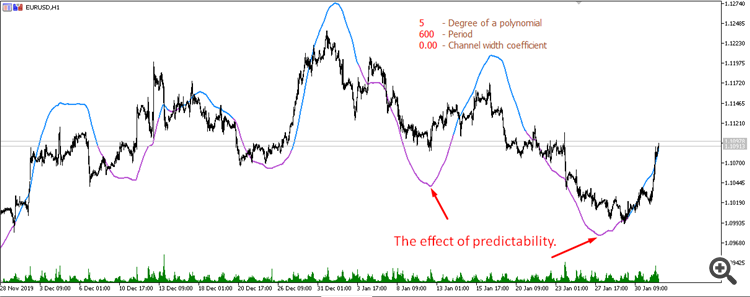
5次多項式からの移動平均（期間600）：


その他


12
新しいコメント