どこに入力すべきかが明確でない。
簡単に説明しますと(すみません、詳細は割愛させていただきますが)
EMAに似た差分方程式で定義される再帰的なフィルターがあり、パラメーターはαである。パラメータは1つだけなので、それを適応する。アイデア:市場の 動きが、ある瞬間に先験的に設定されたモデルに対応しているかどうかをチェックさせる。ここでは念のため「適正比率」(AR)と呼ぶ一定の値を導入し、計算する。0から1まで変化させ、1が完全な「一致」、0が完全な「不一致」に相当する。さらに推論すると、もしKAが1に近いなら、我々のモデルの枠組みの中で予測可能な展開をしているので、市場はあまり「注意深く」監視する必要はないのかもしれない、ということになる。逆にKAが0に近い場合は、市場行動の予測可能性が低下しており、「より慎重に」価格を追跡する必要があると考える。その結果、パラメータαはCAの単調関数であるべきであると結論づけた。依存関係(例:線形)を選択して先に進みましょう。
図からわかるように、トレンドを追いながら(いつも違うけど)、無駄な変動に釘を刺すようなフラットさがなかなかいい。これがどの程度成功しているのか、実体験に基づくどなたかのご意見を伺いたい。
вот из того, что вроде как ближе всего графически: линейно взвешенная(2):
видите - синяя на флетовых участках прыгает, а красная ведет себя гораздо более спокойно. При этом в тренде и там, и там около дела
私は上記で、リニアウェイト3があなたのものよりさらに良い動作をすることを示しましたが、ラグも少ないです。
適応フィルターは、スペクトルを使って行われ、まずスペクトルを検出し、最も高いパワーの周波数から3〜5個の周波数を選んでフィルターにかける。
しかし、特別な成果はないと即答せざるを得ません。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索

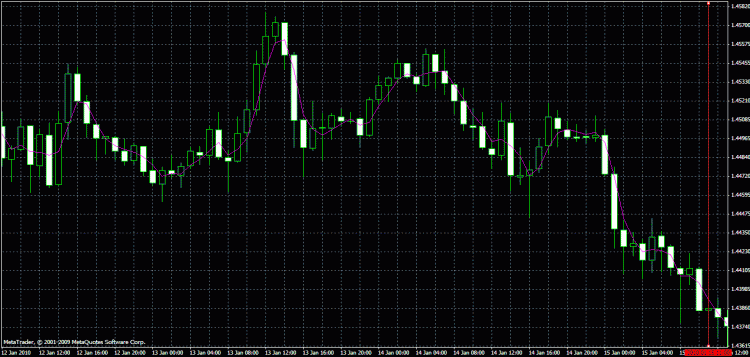

...、DSPで経験したことを少し思い出しています。そして、こんなものができました(さっそくですが、再描画はありません)。
これと密接に関わった人への質問:これ(グラフ)は良いのか悪いのか?