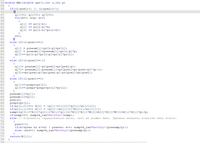
void calcPolynomialRegression(double &PricesArray[],double &RegressionArray[], int power) { ArrayResize(RegressionArray, ArraySize(PricesArray)); ArraySetAsSeries(RegressionArray,ArrayGetAsSeries(PricesArray)); double summ_x_value[21],summ_y_value[11],constant[11],matrix[11][11]; ArrayInitialize(summ_x_value,0); ArrayInitialize(summ_y_value,0); ArrayInitialize(constant,0); ArrayInitialize(matrix,0); double summ=0,summ_x=0,summ_y=0; int pos=ArraySize(PricesArray)-1; summ_x_value[0]=ArraySize(PricesArray); for(int exp_n=1; exp_n<=2*power; exp_n++) { summ_x=0; summ_y=0; for(int k=1; k<=ArraySize(PricesArray); k++) { summ_x+=MathPow(k,exp_n); if(exp_n==1) summ_y+=PricesArray[pos-k+1]; else if(exp_n<=power+1) summ_y+=PricesArray[pos-k+1]*MathPow(k,exp_n-1); } summ_x_value[exp_n]=summ_x; if(summ_y!=0) summ_y_value[exp_n-1]=summ_y; } for(int row=0; row<=power; row++) for(int col=0; col<=power; col++) matrix[row][col]=summ_x_value[row+col]; int initial_row=1; int initial_col=1; for(int i=1; i<=power; i++) { for(int row=initial_row; row<=power; row++) { summ_y_value[row]=summ_y_value[row]-(matrix[row][i-1]/matrix[i-1][i-1])*summ_y_value[i-1]; for(int col=initial_col; col<=power; col++) matrix[row][col]=matrix[row][col]-(matrix[row][i-1]/matrix[i-1][i-1])*matrix[i-1][col]; } initial_col++; initial_row++; } int j=0; for(int i=power; i>=0; i--) { if(j==0) constant[i]=summ_y_value[i]/matrix[i][i]; else { summ=0; for(int k=j; k>=1; k--) summ+=constant[i+k]*matrix[i][i+k]; constant[i]=(summ_y_value[i]-summ)/matrix[i][i]; } j++; } int k=1; for(int i=ArraySize(PricesArray)-1; i>=0; i--) { summ=0; for(int n=0; n<=power; n++) summ+=constant[n]*MathPow(k,n); RegressionArray[i]=summ; k++; } }
J'ai mis en œuvre un calcul de régression (pas seulement linéaire) sans aucun cycle. Plus précisément, un cycle n'est nécessaire qu'une seule fois pendant l'initialisation.
En conséquence, la vitesse de calcul est mille fois plus rapide.
Et le code est plus court.
Mais je suis désolé, je ne vais pas poster le code. C'est un secret.
Je dis juste que c'est réel.
Il y a deux articles qui vous aideront

- www.mql5.com
J'ai implémenté le calcul de la régression (pas seulement linéaire) sans aucune boucle. Pour être plus exact, la boucle n'est nécessaire qu'une seule fois à l'initialisation.
En conséquence, la vitesse de calcul est mille fois plus rapide.
Et le code est plus court.
Mais je suis désolé, je ne vais pas poster le code. C'est un secret.
Je dis juste que c'est réel.
Le code est très simple. On ajoute les carrés actuels, on soustrait les carrés hors de l'intervalle. C'est tout. C'est tout le secret.)
Elle peut être encore plus intéressante, mais en suivant des principes différents.
Le code est très simple. On ajoute les carrés actuels, on soustrait les carrés hors de l'intervalle. C'est tout. C'est le secret.)
C'est drôle.)
Pour rendre la chose encore plus drôle, vous pourriez parler non pas de la chaîne, mais de la façon de faire une ligne de régression polynomiale sans cycles. Mais je ne vais certainement pas faire ça. Vous n'en avez pas besoin.
J'ai mis en œuvre un calcul de régression (pas seulement linéaire) sans aucun cycle. Plus précisément, le cycle n'est nécessaire qu'une seule fois à l'initialisation.
En conséquence, la vitesse de calcul est des milliers de fois plus rapide.
Et le code est plus court.
Mais je suis désolé, je ne vais pas poster le code. C'est un secret.
Je dis juste que c'est réel.
Des milliers de fois plus rapide, et sans boucle de valeurs d'entrée ? ??
Je n'y crois pas ! !!
Au minimum, une boucle des paramètres d'entrée est obligatoire !
J'ai mis en œuvre un calcul de régression (pas seulement linéaire) sans aucun cycle. Plus précisément, la boucle n'est nécessaire qu'une seule fois à l'initialisation.
En conséquence, la vitesse de calcul est mille fois plus rapide.
Et le code est plus court.
Mais je suis désolé, je ne vais pas poster le code. C'est un secret.
Je dis juste que c'est réel.
Et même sans une boucle de sommation x*y ? Et si x et y ne sont pas des lignes droites ?
Des milliers de fois plus rapide, et sans boucle de valeurs d'entrée ? ??
Je n'y crois pas ! !!
Au moins une boucle sur les paramètres d'entrée est obligatoire !
Et même sans une boucle de sommation x*y ? Et si x et y ne sont pas des lignes droites ?
Ne le croyez pas pour ce qu'il vaut.
Rashid a laissé tomber les articles. Lisez-les attentivement. Il y a un lien vers un autre article :
https://www.mql5.com/ru/articles/270
Si vous vous creusez les méninges au niveau des maths de 7ème-8ème année, vous pouvez obtenir l'écart-type pour obtenir le canal, et pas seulement la moyenne glissante, d'une manière similaire sans cycle. Je l'ai implémenté pour un polynôme de n'importe quel degré, pas seulement du premier degré (régression linéaire). Vous pouvez le sentir dans la version de démonstration sur la place de marché.
HH j'ai écrit que la boucle est nécessaire une fois à l'initialisation.
Des milliers de fois plus rapide, y compris pour le calcul de l'écart-type (c'est-à-dire la largeur du canal).- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation
J'ai un indicateur de régression linéaire.
Comment intégrer son calcul dans l'EA et obtenir des données sur 0 barre ou sur 1.
J'ai essayé de faire comme ça :
Mais ça ne donne pas quelque chose...