Discussion de l'article "Modèle de Régression Universel pour la Prévision des Prix du Marché" - page 8
Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
Contactez-nous par message privé pour en savoir plus sur les conditions générales.
Добрый день, уважаемый Юсуфходжа, подскажите, где можно скачать индикаторы и советники о которых вы говорите?
Les indicateurs sont-ils rémunérés ou quelque chose comme ça ? Publiés dans la base de code, utilisez-les à votre guise !
Un nouvel article intitulé "Universal Regression Model for Market Price Prediction" (Modèle de régression universel pour la prédiction des prix du marché ) a été publié :
Auteur : Юсуфходжа
bon article.
très impressionnant
C'est dommage, mais il y a des erreurs au tout début de l'article.
Tout d'abord, l'augmentation du prix à un moment t aura bien sûr une certaine valeur et nous la désignons par D0. Supposons que...
Ensuite... Maintenant, à t=0, je comprends qu'il n'y a pas d'impact sur le prix et apparemment il n'y a pas non plus d'augmentation de prix due à l'impact externe. Cependant, nous avons de nouveau appelé le delta D0.
Nous avons ensuite introduit dt/tau dans la formule, qui est de toute façon 1/C^2, c'est-à-dire que nous avons donné une accélération à l'impact, ce qui fera de toute façon bouger la régression géométrique. Pourquoi devrions-nous le faire ? Après tout, nous n'avons pas encore défini ce qu'est cet impact...
en général.
C'est dommage, mais il y a des erreurs au tout début de l'article.
Tout d'abord, l'augmentation du prix à un moment t aura bien sûr une certaine valeur et nous la désignons par D0. Supposons que...
Ensuite... Maintenant, à t=0, je comprends qu'il n'y a pas d'impact sur le prix et apparemment il n'y a pas non plus d'augmentation de prix due à l'impact externe. Cependant, nous avons de nouveau appelé le delta D0.
Nous avons ensuite introduit dt/tau dans la formule, qui est de toute façon 1/C^2, c'est-à-dire que nous avons donné une accélération à l'impact, ce qui fera de toute façon bouger la régression géométrique. Pourquoi devrions-nous le faire ? Après tout, nous n'avons pas encore défini ce qu'est cet impact...
Eh bien, en général...
1. Do n'est pas l'augmentation du prix, mais le potentiel initial de la force affectant le prix au temps t=0.
2. extrait de l'article : ".... supposons que le prix du marché, qui est en équilibre, ne peut changer que sous l'action d'une force extérieure D(t), dont nous mesurerons l'ampleur et la valeur dans la même dimension que le prix.
Supposons également que la variation du prix du marché P(t) au cours du temps t depuis le début de l'influence de cette force, augmentant continuellement à partir d'une valeur nulle selon une régularité qui nous est encore inconnue, tende à atteindre la valeur P(∞) = D0 à l'infini. Autrement dit, par D0, nous entendons une augmentation ou une diminution finie du prix du marché, en fonction de la nature et du signe de cette force d'influence.
En outre, nous supposons que D(t=0) = D0. Supposons en outre que pendant la période infinitésimale dt, la force d'influence diminuera de la valeur dD(t) proportionnellement à la force restante D(t) à l'instant t :
d'où la dépendance exponentielle de D(t) par rapport au temps t sous la forme suivante :
où :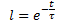
t - temps écoulé depuis le début de l'impact de la force déstabilisatrice en unités de séries temporelles, secondes (min, heures, jours, semaines, décennies, mois, années) ;
τ (tau) - coefficient de proportionnalité, numériquement égal à la constante de temps du processus, en secondes (min, heures, jours, semaines, décennies, mois, années)".
Où avez-vous trouvé la dimensionnalité de 1/s^2 ? Ce rapport n'a aucune dimensionnalité. Je ne l'ai pas glissé, j'ai fait l'hypothèse que le taux de changement (diminution) d' une force agissant sur un processus est proportionnel à la force elle-même, ce qui ne contredit pas la logique, et ensuite, cette hypothèse a été pleinement confirmée. Comme coefficient de proportionnalité, il a introduit le rapport a (alpha) = 1/tau, qui a pour dimension l'inverse du temps. Par a (alpha), j'entends l'impédance du système, c'est-à-dire la résistance du système au flux du processus, et tau est l'image du temps dans les transformations de Laplace, comme il s'est avéré plus tard, et permet de faire passer l'analyse du processus du domaine différentiel au domaine ordinaire. Cela signifie que tout processus a son propre temps, différent du nôtre, et que tau agit comme un "traducteur" de temps, si je puis m'exprimer ainsi. Dans les entrailles de l'article, j'ai donné un moyen d'estimer le tau :
Maintenant, si les valeurs de la fonction f aux moments correspondants du temps t sont connues, alors à partir de cette équation les paramètres n, τ et le coefficient β sont déterminés comme suit :
où :
Les valeurs de la fonction f aux moments correspondants du temps t et du temps t sont déterminées par les valeurs réelles du prix du marché P0, P1,..., Pk aux moments du temps h0, h1,..., һk à partir du début de sa déstabilisation par différenciation numérique, rapportée au milieu de l'intervalle :
f1 = (P1 - P0)/(ch1 - ch0) ; f2 = (P2 - P1)/( ch2- ch1) ; f3 = (P3 - P2)/( ch3- ch2) ; et ainsi de suite ;
t1 = (ch0 + ch1)/2 ; t2 = (ch1 + ch2)/2 ; t3 = (ch3 + ch2)/2 ; etc.