Consejos prácticos, por favor.

Nuevo comentario
 

Pregunta: ¿Cómo puedo evaluar correctamente los resultados?

El error de cada módulo se indica en forma de porcentaje. El 0% es el resultado ideal.

________________ PARÁMETROS ________________ Mod. 1 Mod. 2 Mod. 3 Modo 4 Modo 5 (vi) Modo 6 (vi) Modo 7 (vi) Modo 8 (vi) Mod 9 (vi) Mod 10 (vi) Mod 11 (vi) Mod 12 (viii) mod 13 (vi) 14 Modo 15 Error medio De los intentos
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_HAND 4,43 17,09 15,82 2,53 0,63 17,72 28,48 5,70 13,29 5,70 8,23 6,33 0,63 3,16 6,96 9,11 158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT1 5,06 17,72 12,66 3,80 0,63 19,62 29,11 4,43 9,49 5,06 6,33 6,33 1,90 1,90 6,33 8,69 158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT2 4,43 20,25 16,46 4,43 0,63 17,72 29,75 6,33 5,06 8,23 10,13 5,06 0,63 1,27 4,43 8,99 158,00


Me gustaría que el error de cada módulo fuera mínimo, pero también me gustaría que la dispersión fuera mínima.

 
Сергей Таболин:

Pregunta: ¿Cómo puedo evaluar correctamente los resultados?

El error de cada módulo se indica en forma de porcentaje. El 0% es el resultado ideal.

________________ PARÁMETROS ________________ Mod. 1 Mod. 2 Mod. 3 Modo 4 Modo 5 (vi) Modo 6 (vi) Modo 7 (vi) Modo 8 (vi) Mod 9 (vi) Mod 10 (vi) Mod 11 (vi) Mod 12 (viii) mod 13 (vi) 14 Modo 15 Error medio De los intentos
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_HAND 4,43 17,09 15,82 2,53 0,63 17,72 28,48 5,70 13,29 5,70 8,23 6,33 0,63 3,16 6,96 9,11 158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT1 5,06 17,72 12,66 3,80 0,63 19,62 29,11 4,43 9,49 5,06 6,33 6,33 1,90 1,90 6,33 8,69 158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT2 4,43 20,25 16,46 4,43 0,63 17,72 29,75 6,33 5,06 8,23 10,13 5,06 0,63 1,27 4,43 8,99 158,00


Quiero que el error de cada módulo sea mínimo, pero también quiero que la dispersión sea mínima.

producto de logaritmos

ZS: no estoy muy seguro de lo que se necesita, pero el logaritmo permitirá tratar los errores de forma progresiva, dará mejores resultados en casos individuales (módulos individuales). Y la multiplicación es un intento de reducir la dispersión
 
Alexandr Andreev:

producto de logaritmos

ZS: No entiendo muy bien qué es lo que se necesita exactamente, pero el logaritmo permitirá tratar los errores de forma progresiva, dará mejores resultados en casos puntuales (módulos individuales). Y la multiplicación es un intento de reducir la propagación

Gracias. ¿Yprácticamente cómo es?

 
Сергей Таболин:

Gracias. ¿Yprácticamente cómo es eso?

Probablemente sea el producto de

Opción1 ) Traduzca cada módulo en estilo (1-x%) y multiplíquelo..... la respuesta también se resta de la unidad.

x% es el valor de la celda

Opción 2

Con los logaritmos simplemente tomamos el valor de una celda y contamos el logaritmo a partir de ella)))) cuanto más cerca del valor cero esté la evaluación progresiva, es decir, con algún ajuste de base 0,1 es mejor que 0,01 y también 0,1 es mejor que 1. Sólo habrá un parámetro de base para el logaritmo con el que vale la pena jugar.

 
Alexandr Andreev:

Tal vez un producto simple sería suficiente.

Opción1 ) Traduzca cada módulo al estilo (1-x%) y multiplíquelo..... La respuesta también se resta a la unidad.

x% es el valor de la celda

Opción 2

Con los logaritmos simplemente tomamos el valor de una celda y contamos el logaritmo a partir de ella)))) cuanto más cerca del valor cero esté la evaluación progresiva, es decir, con algún ajuste de base 0,1 es mejor que 0,01 y también 0,1 es mejor que 1. Sólo habrá un parámetro base del logaritmo con el que vale la pena jugar.

Opción 1

-3,43 -16,09 -14,82 -1,53 0,37 -16,72 -27,48 -4,70 -12,29 -4,70 -7,23 -5,33 0,37 -2,16 -5,96 10601305851,38
-4,06 -16,72 -11,66 -2,80 0,37 -18,62 -28,11 -3,43 -8,49 -4,06 -5,33 -5,33 -0,90 -0,90 -5,33 -6223799946,09
-3,43 -19,25 -15,46 -3,43 0,37 -16,72 -28,75 -5,33 -4,06 -7,23 -9,13 -4,06 0,37 -0,27 -3,43 1237520122,21


¿Qué me dice esto?

Opción 2

-0,64640373 -1,23274206 -1,19920648 -0,40312052 0,200659451 -1,24846372 -1,45453998 -0,75587486 -1,12352498 -0,75587486 -0,91539984 -0,80140371 0,200659451 -0,49968708 -0,84260924
-0,70415052 -1,24846372 -1,10243371 -0,5797836 0,200659451 -1,292699 -1,46404221 -0,64640373 -0,97726621 -0,70415052 -0,80140371 -0,80140371 -0,2787536 -0,2787536 -0,80140371
-0,64640373 -1,30642503 -1,21642983 -0,64640373 0,200659451 -1,24846372 -1,47348697 -0,80140371 -0,70415052 -0,91539984 -1,00560945 -0,70415052 0,200659451 -0,10380372 -0,64640373


Este es el logaritmo con base 0.1

¿Qué debo hacer con él?

He probado otras funciones. ¿Sólo que cómo los entiendo yo también? ....

STANDOTCLONE 7,8208
7,9133
8,4150
DISP.B 61,1650
62,6198
70,8128
QUADROTKL 856,3093
876,6772
991,3799
MEDIANA 6,3300
6,3300
5,0600
SCOS 1,1805
1,5197
1,3018
EXCESO 1,1322
1,9702
1,1832
 
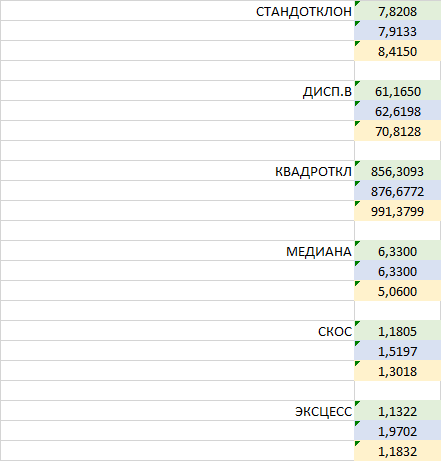
Encuentre el máximo en cada fila, luego seleccione la fila con el máximo mínimo. Perdón por el juego de palabras))
 
Dmitry Fedoseev:
Encuentre el máximo de cada fila, y luego elija la fila con el máximo mínimo. Perdón por el juego de palabras))

Máximo en la línea 3, mínimo en la línea 1. И? )))

 
Сергей Таболин:

Máximo en la línea 3, mínimo en la línea 1. И? )))

Elija la primera línea.

 
Сергей Таболин:

Opción 1

-3,43 -16,09 -14,82 -1,53 0,37 -16,72 -27,48 -4,70 -12,29 -4,70 -7,23 -5,33 0,37 -2,16 -5,96 10601305851,38
-4,06 -16,72 -11,66 -2,80 0,37 -18,62 -28,11 -3,43 -8,49 -4,06 -5,33 -5,33 -0,90 -0,90 -5,33 -6223799946,09
-3,43 -19,25 -15,46 -3,43 0,37 -16,72 -28,75 -5,33 -4,06 -7,23 -9,13 -4,06 0,37 -0,27 -3,43 1237520122,21


¿Qué me dice esto?

Opción 2

-0,64640373 -1,23274206 -1,19920648 -0,40312052 0,200659451 -1,24846372 -1,45453998 -0,75587486 -1,12352498 -0,75587486 -0,91539984 -0,80140371 0,200659451 -0,49968708 -0,84260924
-0,70415052 -1,24846372 -1,10243371 -0,5797836 0,200659451 -1,292699 -1,46404221 -0,64640373 -0,97726621 -0,70415052 -0,80140371 -0,80140371 -0,2787536 -0,2787536 -0,80140371
-0,64640373 -1,30642503 -1,21642983 -0,64640373 0,200659451 -1,24846372 -1,47348697 -0,80140371 -0,70415052 -0,91539984 -1,00560945 -0,70415052 0,200659451 -0,10380372 -0,64640373


Este es el logaritmo con base 0.1

¿Qué debo hacer con él?

He probado otras funciones. ¿Pero cómo los entiendo yo también?

El error de cada módulo se da en porcentaje. El 0% es el resultado ideal". El número 1 significa 100% - x% o 1-X*0,01

 
@Sergey Tabolin @Sergey Tabolin
TOTAL
0,9557 0,8291 0,8418 0,9747 0,9937 0,8228 0,7152 0,943 0,8671 0,943 0,9177 0,9367 0,9937 0,9684 0,9304 0,77439
0,9494 0,8228 0,8734 0,962 0,9937 0,8038 0,7089 0,9557 0,9051 0,9494 0,9367 0,9367 0,981 0,981 0,9367 0,758606
0,9557 0,7975 0,8354 0,9557 0,9937 0,8228 0,7025 0,9367 0,9494 0,9177 0,8987 0,9494 0,9937 0,9873 0,9557 0,771806

la segunda línea es la mejor, y la primera y la tercera son muy similares

el total restado a la unidad, es decir, cuanto más cercano a 0 sea el total, mejores serán los resultados..... en otras palabras, los resultados hasta ahora no son muy buenos porque 0,75 es su 75, aunque depende de con qué se compare..... la peor puntuación sería 1 (100%) la mejor puntuación 0

Tienes que entender que una puntuación de 90 es diez veces mejor que una puntuación de 99.... una puntuación de 99 es diez veces mejor que una puntuación de 99,9... 100 es de hecho posible sólo cuando todos los módulos tienen una puntuación de error de 100... Es decir, una puntuación de 0,1 es diez veces peor que una puntuación de 0,01. Al mismo tiempo, una puntuación de 10 es diez veces peor que una puntuación de 1.



con el logaritmo sobre think..... la respuesta debe ser exclusivamente valores positivos... normalmente un logaritmo de 1,1... en el rango de 1 a 2, no de 0 a 1.... si quieren aumentar el número y de 2 si quieren disminuirlo progresivamente


El método de desviación cuadrática está definitivamente descartado. Lo mismo ocurre con todas las demás que cuentan con desviaciones. Porque lo ideal sería utilizar la desviación cuadrática de una regresión lineal para entender la varianza. Pero entonces obtenemos una estimación de estas desviaciones sin ninguna media de los propios números.....

 
Сергей Таболин:

Pregunta: ¿Cómo puedo evaluar correctamente los resultados?

El error de cada módulo se indica en forma de porcentaje. El 0% es el resultado ideal.

________________ PARÁMETROS ________________ Mod. 1 Mod. 2 Mod. 3 Modo 4 Modo 5 (vi) Modo 6 (vi) Modo 7 (vi) Modo 8 (vi) Mod 9 (vi) Mod 10 (vi) Mod 11 (vi) Mod 12 (viii) mod 13 (vi) 14 Modo 15 Error medio De los intentos
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_HAND 4,43 17,09 15,82 2,53 0,63 17,72 28,48 5,70 13,29 5,70 8,23 6,33 0,63 3,16 6,96 9,11 158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT1 5,06 17,72 12,66 3,80 0,63 19,62 29,11 4,43 9,49 5,06 6,33 6,33 1,90 1,90 6,33 8,69 158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT2 4,43 20,25 16,46 4,43 0,63 17,72 29,75 6,33 5,06 8,23 10,13 5,06 0,63 1,27 4,43 8,99 158,00


Quiero que el error de cada módulo sea mínimo, pero también quiero que la dispersión sea mínima.

Probablemente sea mejor obtener la suma de cuadrados de los errores del módulo y extraer la raíz.
Así, obtendremos la estimación del error total del módulo.
Cuanto más cercano a cero sea este valor, mejor.
Así que es así.

//+------------------------------------------------------------------+
//|                                                EstimateError.mq5 |
//|                        Copyright 2020, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2020, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"


double ModN[15][3] = {{4.43, 5.06, 4.43},
                      {17.09, 17.72, 20.25},
                      {15.82, 12.66, 16.46},
                      {2.53, 3.80, 4.43},
                      {0.63, 0.63, 0.63},
                      {17.72, 19.62, 17.72},
                      {28.48, 29.11, 29.75},
                      {5.70, 4.43, 6.33},
                      {13.29, 9.49, 5.06},
                      {5.70, 5.06, 8.23},
                      {8.23, 6.33, 10.13},
                      {6.33, 6.33, 5.06},
                      {0.63, 6.33, 0.63},
                      {3.16, 1.90, 1.27},
                      {6.96, 6.33, 4.43}};

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
{
   double ModX[];
   ArrayResize(ModX, 3);
   ZeroMemory(ModX);   
   
   int    num = 1;
   double est = 0.0;
   
   for(int i=0; i<15; i++)
   {
      for(int j=0; j<3; j++)
      {
         ModX[j] = ModN[i][j];         
      }
         
      est = EstimateError(ModX);  
      
      PrintFormat("Mod"+(string)num+" EstimateError: %.3f", est); 
      num++;
   }         
}// End OnStart

//+------------------------------------------------------------------+
double EstimateError(double & arr[])
{
   int size = ArraySize(arr);
   if(size == 0 || size < 3) 
      return(0.0);
   
   //double avg       = ArrayMean(arr); 
   double max       = ArrayMax(arr);   
   double min       = ArrayMin(arr); 
   double sum_sqr_e = 0.0;
   double est_e     = 0.0;      
   
   
   for(int i=0; i<size; i++)   
      sum_sqr_e += MathPow(arr[i] - (max-min)/* или avg*/, 2.0) / (size - 2.0);
      
   est_e = MathSqrt(sum_sqr_e);   

   return(est_e);
}

//+-------------------------------------------------------------------
//Возвращает максимальное значение элементов массива
double ArrayMax(double & arrIn[])
{
   uint size = ArraySize(arrIn);
   if(size == 0) 
      return(0.0);          
   
   double max = arrIn[0];
   for(uint i=1; i<size; i++)
      if(arrIn[i] > max) 
         max = arrIn[i];

   return(max);
}

//--------------------------------------------------------------------
//Возвращает минимальное значение элементов массива
double ArrayMin(double & arrIn[])
{
   uint size = ArraySize(arrIn);
   if(size == 0) 
      return(0.0);   
   
   double min = arrIn[0];  
   for(uint i=1; i<size; i++)
      if(arrIn[i] < min) 
         min = arrIn[i];

   return(min);
}

//--------------------------------------------------------------------
//Возвращает средне арефметическое значение элементов массива
double ArrayMean(double & arrIn[])
{
   uint size = ArraySize(arrIn);
   if(size == 0) 
      return(0.0);         

   double sum = 0.0;       
   for(uint i=0; i<size; i++) 
      sum += arrIn[i];     
   
   return(sum/size);
}

//--------------------------------------------------------------------

2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod1 EstimateError: 6.965
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod2 EstimateError: 26.422
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod3 EstimateError: 19.577
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod4 EstimateError: 3.226
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod5 EstimateError: 1.091
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod6 EstimateError: 28.540
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod7 EstimateError: 48.234
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod8 EstimateError: 6.361
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod9 EstimateError: 6.102
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod10 EstimateError: 5.965
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod11 EstimateError: 8.130
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod12 EstimateError: 8.098
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod13 EstimateError: 7.198
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod14 EstimateError: 1.413
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod15 EstimateError: 6.138

La estimación muestra que Mod5 tiene el menor error.

1234567
Nuevo comentario